2. 中国科学院大学,北京 100049
青藏高原在亚洲季风中扮演了重要角色[1],青藏高原的气候变化不仅直接驱动中国东部和西南部气候的变化[2-3],而且对整个亚洲和北半球也有巨大影响[4],甚至对全球气候变化也具有明显的敏感性、超前性和调节性。此外,青藏高原的地气物理过程对全球气候异常、东亚大气环流及中国灾害性天气的发生发展有重大影响[5]。青藏高原的热力作用是由地气相互作用决定的。地气之间的能量和物质交换是决定气候状态和大气环流特征的最主要物理过程之一,而定量描述地面的热力过程、土壤热传导和土壤热输送是数值预报和气候模式物理中陆面过程参数化的任务之一[6]。土壤的热力学性质影响着地表和大气之间的物质和能量交换,对地球大气边界层物理过程、大气环流和区域气候产生重要影响,正确地模拟土壤温度和热通量是陆面物理过程模式、大气环流模式、区域气候模式数值模拟研究的重要环节之一[7-9]。因此,深入研究土壤的有关物理参数(土壤热扩散率、土壤热传导率、土壤体积热容等)有利于更好地分析能量分配,从而为利用一维、中尺度和大尺度模式模拟地气相互作用和天气过程提供参数化方案[10]。土壤热扩散率是计算土壤热通量的输入项,土壤中热量的传输是陆面过程的一部分,也是影响地表能量平衡的重要因素之一,土壤中热量的吸收和损失均与气候变化息息相关[11]。因此,对土壤热扩散率时空分布的研究,有利于深刻认识土壤热通量的物理过程,为各种天气、气候及生态模型的建立和检验提供重要参数和理论支持[12]。
由于受观测技术和观测资料的限制,国内外对土壤热扩散率的观测研究并不多。因为土壤的热扩散率取决于诸多因素,如土壤质地、矿物组成、含盐量和土壤含水量等[13-16],使得热参数的估计非常困难。许多研究人员试图通过在实验室条件下使用土壤含水量、密度和形状因子来参数化某些土壤的热扩散率[17-18],然而,由于尺度效应[19]和土壤形状、颗粒大小以及包装等的复杂影响[20],当实验室结果外推至田间实验时,通常会产生误差。为了避免这些误差,开发了使用土壤温度观测数据估计土壤热扩散率的方法[21-23]。董文杰和汤懋苍[24]用相位差法计算了多年平均土壤热扩散率,分析了我国土壤热流场与深层大地热流场的关系。1993年王宝灵和汤懋苍[25]用谐波法计算了土壤的导温率,并分析了我国土壤热流的空间分布。范新岗和汤懋苍[26]利用同时考虑了土壤热传输和土壤水分热对流的热传导对流法计算了土壤的热扩散率,得出了传导热通量与对流热通量具有相同的量级,且分析了热通量与地震的关系。高志球等[27]用不同方法求出了土壤热传导方程的解析解,并对那曲地区土壤热扩散率的变化进行了分析。缪育聪等[28]用谐波法、振幅法、相位法和热传导对流法计算了5~20 cm的土壤热扩散率,发现热传导对流法的拟合效果好于振幅法和相位法,在理论上能够更好地反映土壤中的热传输过程。
以上学者的研究基本均是通过理论分析,或者对浅层土壤或者局限于某一区域的土壤热扩散率的分析研究,对整个青藏高原的研究并不多。在诸多模式研究中也将不同土壤类型的土壤热扩散率取为定值[29],但实际上相同土壤类型的土壤热扩散率也有其年际变化和空间变化。目前尚无对青藏高原土壤热扩散率空间分布的研究。本研究利用实测土壤温度资料和热传导对流法分析了青藏高原深层土壤热扩散率的时空分布特征。
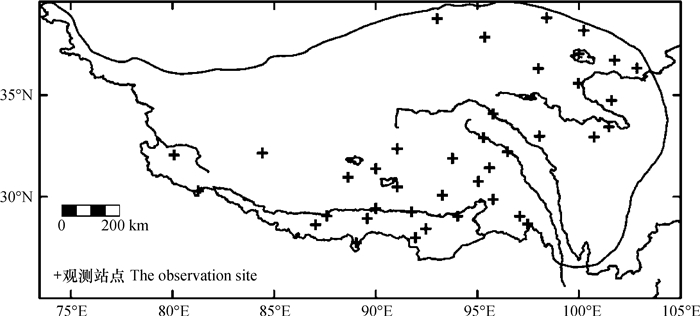
1 材料与方法 1.1 土壤温度资料来源本研究利用青藏高原39个气象站(如图 1)实测的0.8 m和3.2 m深的月平均土壤温度,资料年限为1980—2001年。本资料来自中国气象局,资料选择的依据是:(1)此39个站点土壤温度资料相对齐全、无缺测;(2)80 cm以上各层地温因受大气的强烈影响,难以说明深层变化,而且0.8 m和3.2 m两层深度是中国气象局地面观测的规范深度,包括了0.8 m~1.6 m和1.6 m~3.2 m两个深度。通过计算,得到土壤热扩散率的月和季平均值,对青藏高原土壤热扩散率的时空分布特征进行分析。
|
图 1 青藏高原土壤温度观测站点分布图 Fig. 1 Distribution of observation site in the Qinghai-Tibetan Plateau |
计算土壤热扩散率的方法有很多,如振幅法、相位法、谐波法和热传导对流法等。本文采用热传导对流法,因为土壤的热传输过程包含了热传导和多孔介质热对流两个过程[30]。Gao等[31]指出土壤温度的日变化不仅受土壤热传导作用的影响,还与土壤中液态水热对流作用有关,给出了耦合热传导与热对流的一维热传导对流方程,并利用一阶谐波模型推导出了热传导对流方程的解析解和土壤热扩散率的计算公式。Gao等[32-33]利用青藏高原和黄土高原等地的土壤温度资料,验证了热传导对流法的可靠性,认为热传导对流法能更好地描述土壤中的热传输物理过程。在以上理论的基础上发展了一套包括热传导和热对流的计算土壤热通量方法[31],该方法可以利用气象站地温资料反演获得地热流场信息,从热传导方程和热对流方程出发推导出了包括传导和对流的线性传热方程:
| $ \frac{{\partial T}}{{\partial t}} = K\frac{{{\partial ^2}T}}{{\partial {z^2}}} - W\frac{{\partial T}}{{\partial z}} $ | (1) |
式中,T为土壤温度,℃;t为时间,s;K为土壤热扩散率,m2 s-1,K=λ/Cg,其中Cg为土壤体积热容,J cm-3℃-1,λ为热传导率,W m-1 C-1;
| $ T\left( {{z_0},{\rm{ }}t} \right) = \bar T{|_{z = {z_0}}} + A{\rm{sin}}\left( {\omega t + \beta } \right) $ | (2) |
式中,T为土壤深度z0处的月平均温度,β为z0处温度相位。可以推导出式(1)的解析解和土壤热扩散率K与垂直对流速度W的计算公式[32]:
| $ T\left( {z,{\rm{ }}t} \right) = \bar T\left( z \right) + A{\rm{exp}}\left[ { - M\left( {z - {z_0}} \right)} \right] \times {\rm{sin}}\left[ {\omega t + \beta + N\left( {{z_0} - z} \right)} \right] $ | (3) |
| $ K = \frac{{{{\left( {{z_1} - {z_2}} \right)}^2}\omega \ln \left( {{A_2}/{A_1}} \right)}}{{\left( {{\phi _2} - {\phi _1}} \right)\left[ {{{\left( {{\phi _2} - {\phi _1}} \right)}^2} + {{\left( {\ln \left( {{A_2}/{A_1}} \right)} \right)}^2}} \right]}} $ | (4) |
| $ W = \frac{{\omega \left( {{z_1} - {z_2}} \right)}}{{{\phi _2} - {\phi _1}}}\left[ {1 - \frac{{2{{\left( {\ln \left( {{A_2}/{A_1}} \right)} \right)}^2}}}{{{{\left( {{\phi _2} - {\phi _1}} \right)}^2} + {{\left( {\ln \left( {{A_2}/{A_1}} \right)} \right)}^2}}}} \right] $ | (5) |
其中,
| $ M = - \frac{W}{{2K}} + \frac{{\sqrt 2 }}{{4K}}\sqrt {{W^2} + \sqrt {{W^4} + 16{K^2}{\omega ^2}} } $ | (6) |
| $ N = \frac{{\sqrt 2 \omega }}{{\sqrt {{W^2} + \sqrt {{W^4} + 16{K^2}{\omega ^2}} } }} $ | (7) |
式中,ω为年变化周期,ω=2π/p(rad·s-1),p为z0处土壤温度的变化周期。A1、A2、φ1、φ2分别为深度z1、z2处的土壤温度振幅和相位(z1< z2)。在深度为z1至z2的土壤层中,求出的土壤热扩散率为一个常数。此外,由式(2)和式(3)可知,任意深度的土壤温度均可用一个正弦函数来表示,则深度为z1和z2的土壤温度实测值可以表示为:
| $ T\left( {{z_1},{\rm{ }}t} \right) = \bar T\left( {{z_1}} \right) + {A_1}{\rm{sin}}\left( {\omega t + {\varphi _1}} \right) $ | (8) |
| $ T\left( {{z_2},{\rm{ }}t} \right) = \bar T\left( {{z_2}} \right) + {A_{\rm{2}}}{\rm{sin}}\left( {\omega t + {\varphi _2}} \right) $ | (9) |
本文利用0.8 m和3.2 m两层土壤温度资料,由最小二乘法拟合求式(8)和式(9)得振幅和相位,再利用式(4)求出土壤热扩散率。
2 结果与讨论利用热传导对流法计算了青藏高原39个气象站各站点1980—2001年的多年月平均土壤热扩散率和多年季节平均土壤热扩散率。在季节划分上,本文仍以3月—5月为春季,6月—8月为夏季,9月—11月为秋季,12月—次年2月为冬季。
由于土壤特性和气候特征的差异,青藏高原地区土壤热扩散率在时空上表现为非均匀性。因此,本文根据各站土壤热扩散率的多年月平均值和多年季平均值分析了青藏高原土壤热扩散率的时空分布特征。
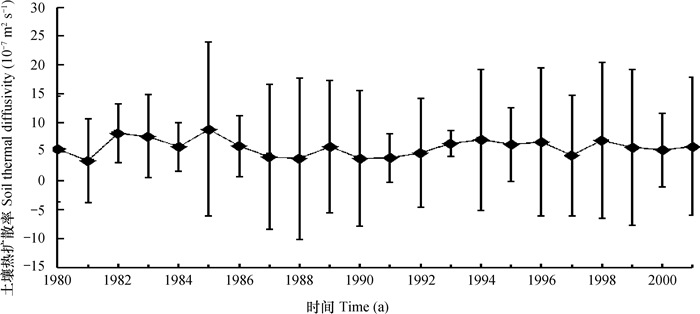
2.1 青藏高原土壤热扩散率年际变化特征用热传导对流法计算的青藏高原土壤热扩散率K的年际变化如图 2所示,可以看出,土壤热扩散率在20世纪90年代以前波动较大,在1991—2001年有小幅度波动。K的年际变化范围为3.4×10-7 m2 s-1~8.9×10-7 m2 s-1。根据杨玮等[34]的研究,1980—2001年青藏高原的长期降水变化也呈现出1990年之前波动较大,90年代之后波动较小的趋势,说明土壤热扩散率的年际变化与降水的年际变化较为相似。青藏高原土壤热通量的这种变化趋势还与张雯等[35]研究的青藏高原土壤湿度的年际变化特征一致。根据邵明安等[36]的研究,土壤热扩散率与土壤含水量有关,开始会随着土壤含水量的增加而增加,达到一定程度之后反而随着土壤含水量的增加而减小。此外,图 2给出了土壤热扩散率标准差的变化,标准差反映的是离散程度大小。可以看出,每年的标准差各不相同,说明土壤热扩散率的变化不同。1993年标准差较小,说明1993年土壤热扩散率变化小,即空间差异小。而1985年土壤热扩散率的标准差相对较大,说明土壤热扩散率变化大,即空间差异大,出现这种现象的原因可能与该年青藏高原各地区降水量的不同有关,这种关系值得进一步研究。
|
图 2 1980—2001年青藏高原平均土壤热扩散率的年际变化 Fig. 2 Mean inter-annual variation of soil thermal diffusivity in Qinghai-Tibetan Plateau during the period from 1980 to 2001 |
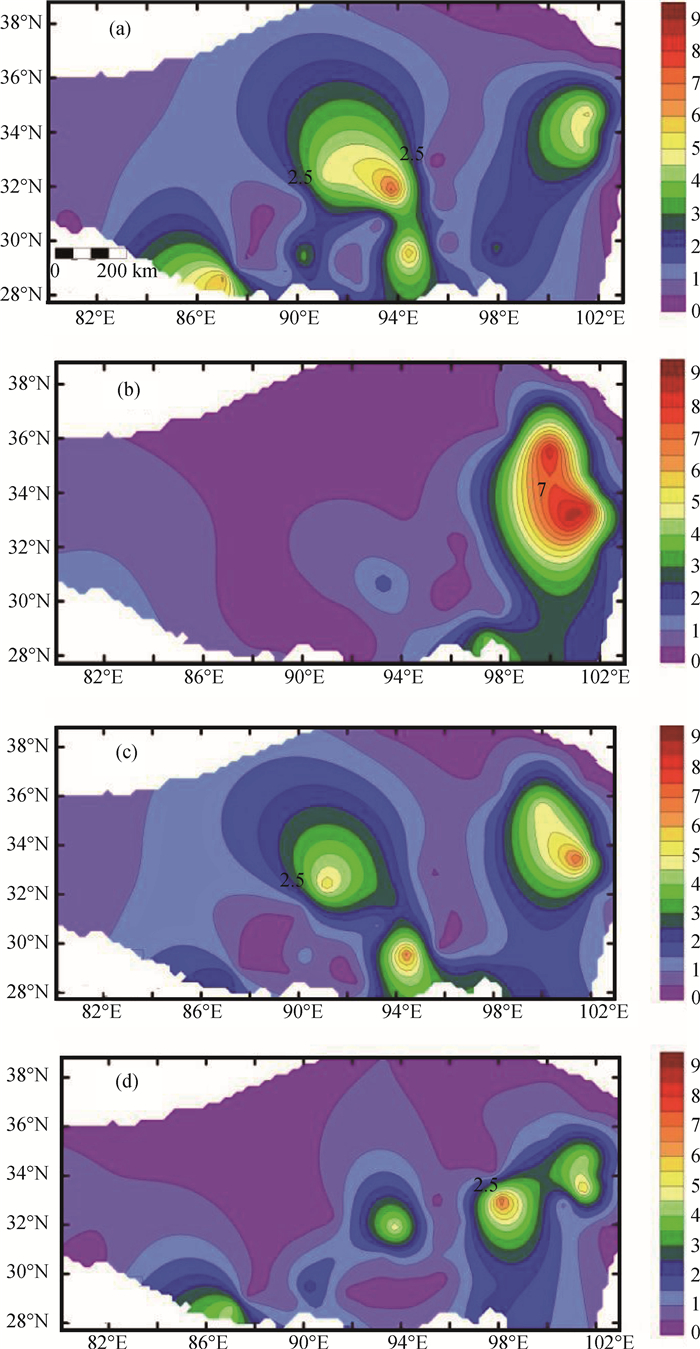
图 3为青藏高原不同季节多年平均土壤热扩散率的空间分布。从图中可以看出,春季(图 3(a))西南部、中部和东部小部分地区的土壤热扩散率为相对高值区,最大值出现在藏北高原那曲东部、怒江上游的南姜塘大湖盆区,达6×10-6 m2 s-1。其余部分为相对低值区,土壤热扩散率的范围为1.3×10-7 m2 s-1~9.2×10-7 m2 s-1。夏季(图 3(b))青藏高原东部小部分仍为相对高值区,最大值出现在青、川、甘三省的交界处,为8×10-6 m2 s-1,土壤热扩散率相对春季有所增大;其余大部分地区的土壤热扩散率减小,范围为1.21×10-7 m2 s-1~7.4×10-7 m2 s-1,特别是青藏高原北部地区土壤热扩散率减小明显。该地区位于长江河源高平原连续多年冻土区。根据土壤的不同冻融过程,在春季处于升温期、夏季处于融化期,冰的导热率几乎是水导热率的4倍,因而冻土的导热率大于融土的导热率,而土壤体积热容的取值与季节无关,是由土壤类型决定的[37]。青藏高原北部地区主要为粉砂土[38],土壤的体积热容相对固定,因此会出现夏季导温率较冬季导温率小。位于青海省和甘肃省西南部、四川西部的青藏高原东部地区为高原亚寒带湿润气候区,海拔在3000 m以上,地势复杂,受高原季风影响年降水量400~780 mm,并主要集中在夏季。而土壤热扩散率的大小主要受质地和含水量的影响,含水量在夏季增大,因此,青藏高原东部土壤热扩散率的最大值出现在夏季。
|
图 3 不同季节土壤热扩散率的空间分布 Fig. 3 Spatial distribution of soil thermal diffusivity relative to season 注:图例单位为10-6 m2 s-1。(a).春季;(b).夏季;(c).秋季;(d).冬季 Note: The unit in the legend is 10-6 m2 s-1. (a). stands for spring; (b). for summer; (c). for autumn; and (d). for winter |
秋季(图 3(c))东部小部分地区的土壤热扩散率开始减小,但仍为相对高值区,最大值为6.2×10-6 m2 s-1;中部地区也为相对高值区,其他地区的土壤热扩散率相对夏季有所增大,土壤热扩散率的变化范围为1.3×10-7 m2 s-1~8.9×10-7 m2 s-1。冬季(图 3(d)),青藏高原大部分地区的土壤热扩散率均减小,西南部、中部和东部小部分地区为相对高值区,最大值为5.1×10-6 m2 s-1。从秋季至冬季寒冷干燥、降水量减小,因而东部小部分地区土壤热扩散率减小;而其余大部分地区的土壤热扩散率减小是因为从秋季至冬季土壤温度减小至零度以下。根据Inaba[39]的实验,在负温度范围内,土壤有效导热率的测量值强烈依赖于土壤温度、含水量及粒度,对于细粒土壤而言,导热率随负温的降低而减小。并且,在冬季,未冻结的水含量较小,所以土壤热扩散率减小。
此外,从冬季和夏季分布图可以看出,冬季高原中北部地区的土壤热扩散率较夏季大,因为此地区位于巴颜喀拉山脉南麓,该地区积雪覆盖时间高达40 d左右,积雪的出现会阻挡热量的交换,使深层温度下降小,而在此期间土壤热通量有小幅度增大,导致土壤热扩散率增大。
2.3 青藏高原多年平均土壤热扩散率空间分布特征图 4给出1980—2001年青藏高原土壤热扩散率的多年平均值空间分布,可以看出,青藏高原大部分地区土壤热扩散率的量级为10-7 m2 s-1,中部和东部小部分地区为相对高值区,量级为10-6 m2 s-1。

|
图 4 1980—2001年青藏高原土壤热扩散率多年平均值空间分布 Fig. 4 Spatial distribution of annual mean of soil thermal diffusivity in the Qinghai-Tibetan Plateau in 1980—2001 注:图例单位为10-6 m2 s-1 Note: The unit in the legend is 10-6 m2 s-1 |
受地理位置、土壤特性、含水量和积雪日数等因素的影响,在西藏那曲东北部的青藏高原中部地区和东部地区为高原亚寒带湿润气候区,由于降水较多,土壤含水量较大,为土壤热扩散率的高值区。祁连山地区为低值区,该地区为高原高寒带半干旱气候,为多年冻土区,含水量少,土壤热扩散率范围在1×10-7~4.8×10-7 m2 s-1。
3 结论利用实测土壤温度资料分析了青藏高原土壤热扩散率在时空上的分布规律,对土壤热扩散率变化特征进行了研究,得到如下结论:土壤热扩散率在20世纪90年代前期波动较大,在1991—2001年有小幅度波动;受气候要素、土壤特性和含水量的影响,土壤热扩散率在空间上的分布是不同的。青藏高原东部地区,从春季至夏季土壤热扩散率增大,夏季至冬季土壤热扩散率逐渐减小;除青藏高原东部以外的其他地区,从春季至夏季土壤热扩散率减小,夏季至秋季土壤热扩散率增大,秋季至冬季土壤热扩散率减小。青藏高原土壤热扩散率月平均最大值出现在青海省和甘肃省西南部以及四川西部的青藏高原东部地区。青藏高原中部的那曲东北部为相对高值区,其他区域为相对低值区,土壤热扩散率的最低值分布在祁连山脉地区。青藏高原大部分地区土壤热扩散率的量级为10-7 m2 s-1,中部和东部小部分地区为相对高值区,量级为10-6 m2 s-1。
| [1] |
Krishnamurti TN, Ramanathan Y. Sensitivity of the monsoon onset to differential heating . Journal of the Atmospheric Sciences, 1982, 39(6): 1090-1306.
(  0) 0) |
| [2] |
吴国雄, 段安民, 刘屹岷, 等. 关于亚洲夏季风爆发的动力学研究的若干近期进展. 大气科学, 2013, 37(2): 212-227. Wu G X, Duan A M, Liu YM, et al. Recent advances in the study on the dynamics of the Asian summer monsoon onset (In Chinese). Chinese Journal of Atmospheric Sciences, 2013, 37(2): 212-227. (  0) 0) |
| [3] |
Liu Y M, Bao Q, Duan A M, et al. Recent progress in the impacy of the Tibetan Plateau on climate in China . Advances in Atmospheric Sciences, 2007, 24(6): 1060-1076. DOI:10.1007/s00376-007-1060-3
(  0) 0) |
| [4] |
吴国雄, 刘屹岷, 刘新, 等. 青藏高原加热如何影响亚洲的气候格局. 大气科学, 2005, 29(1): 47-56. Wu G X, Liu Y M, Liu X, et al. How the heating over Tibetan Plateau affects the Asian climate in summer (In Chinese). Chinese Journal of Atmospheric Sciences, 2005, 29(1): 47-56. (  0) 0) |
| [5] |
温克刚, 陶诗言, 徐祥德, 等. 第二次青藏高原大气科学试验理论研究进展(一). 北京: 气象出版社, 1999. Wen K G, Tao S Y, Xu X D, et al. Progress in theoretical research on the TIPEX(Ⅰ) (In Chinese). Beijing: Chinese Meteorological Press, 1999. (  0) 0) |
| [6] |
叶笃正, 曾庆存, 郭裕福. 当代气候研究. 北京: 气象出版社, 1991. Ye D Z, Zeng Q C, Guo Y F. Study of contemporary climate (In Chinese). Beijing: China Meteorological Press, 1991. (  0) 0) |
| [7] |
刘树华, 潘英, 胡非, 等. 沙漠绿洲地区夏季地表能量收支的数值模拟. 地球物理学报, 2009, 52(5): 1197-1207. Liu S H, Pan Y, Hu F, et al. Numerical simulation of summer land surface energy budget in desert and oasis regions (In Chinese). Chinese Journal of Geophysics, 2009, 52(5): 1197-1207. (  0) 0) |
| [8] |
薛彦广, 高志球, 沙文钰. 利用简单生物圈模式SiB2模拟青藏高原地表能量收支. 大气科学, 2010, 34(1): 131-142. Xue Y G, Gao Z Q, Sha W Y. Modeling of surface energy budget in the Tibetan Plateau using simple biosphere model SIB2 (In Chinese). Chinese Journal of Atmospheric Sciences, 2010, 34(1): 131-142. (  0) 0) |
| [9] |
王介民, 王维真, 刘绍民, 等. 近地层能量平衡闭合问题--综述及个例分析. 地球科学进展, 2009, 24(7): 705-713. Wang J M, Wang W Z, Liu S M, et al. The problems of surface energy balance closure-Anoverview and case study (In Chinese). Advances in Earth Science, 2009, 24(7): 705-713. (  0) 0) |
| [10] |
Gao Z, Chae N, Kim J. Simulation of surface temperature, water balance and soil wetness in the Tibetan Prairie using the simple biosphere model 2// Proceedings of the Second Session of International Workshop on TIPEX-GAME/TIBET. Kunming, China, 2000, 32-34
(  0) 0) |
| [11] |
徐兆生, 马玉堂. 青藏高原土壤热通量的测量、计算和气候学推广方法//青藏高原气象科学实验文集编辑组. 青藏高原气象科学实验文集(二). 北京: 科学出版社, 1984: 24-34 Xu Z S, Ma Y T. Soil heat flux measurements, calculations and climatology promotion methods in Tibetan Plateau(In Chinese)//Editor Group of the Corpus of the Scientific Experiments on the Meteorology in Qinghai-Tibet Plateau. The corpus of the scientific experiments on themeteorology in Qinghai-Tibet Plateau(Ⅱ). Beijing: Science Press, 1984: 24-34 (  0) 0) |
| [12] |
韦志刚, 文军, 吕世华, 等. 黄土高原陆-气相互作用预实验及其晴天地表能量特征分析. 高原气象, 2005, 24(4): 545-555. Wei Z G, We nJ, Lü S H, et al. A primary field experiment of land-atmosphere interaction over the Loess Plateau and its ground surface energy in clear day (In Chinese). Plateau Meteorology, 2005, 24(4): 545-555. (  0) 0) |
| [13] |
Kunii D, Smith J M. Heat transfer characteristics of porous rocks . Aiche Journal, 1960, 6(1): 71-78. DOI:10.1002/(ISSN)1547-5905
(  0) 0) |
| [14] |
Riha S J, McInnes K, Childs S, et al. A finite element calculation for determining thermal conductivity . Soil Science Society of America Journal, 1980, 44(6): 1323-1325. DOI:10.2136/sssaj1980.03615995004400060039x
(  0) 0) |
| [15] |
Campbell G S. Soil physics with BASIC: Transport models for soil-plant systems(Development in soil science 14). Amsterdam: Elsevier, 1985
(  0) 0) |
| [16] |
Noborio K, McInnes K. Thermal conductivity of salt-affected soils . Soil Science Society of America Journal, 1993, 57(2): 329-334. DOI:10.2136/sssaj1993.03615995005700020007x
(  0) 0) |
| [17] |
Webb J. Thermal conductivity of soil . Nature, 1956, 177(4517): 989-989.
(  0) 0) |
| [18] |
Abu-Hamdeh N H, Reeder R C. Soil thermal conductivity effects of density, moisture, salt concentration, and organic matter . Soil Science Society of America Journal, 2000, 64(4): 1285-1290. DOI:10.2136/sssaj2000.6441285x
(  0) 0) |
| [19] |
Barrios M, Francés F. Spatial scale effect on the upper soil effective parameters of a distributed hydro logical model . Hydrological Processes, 2012, 26(7): 1022-1033. DOI:10.1002/hyp.v26.7
(  0) 0) |
| [20] |
Evett S R, Agam N, Kustas W P, et al. Soil profile method for soil thermal diffusivity, conductivity and heat flux: Comparison to soil heat flux plates . Advances in Water Resources, 2012, 50: 41-54. DOI:10.1016/j.advwatres.2012.04.012
(  0) 0) |
| [21] |
Horton R, Wierenga P J. Evaluation of methods for determining the apparent thermal diffusivity of soil near the surface . Soil Science Society of America Journal, 1983, 47(1): 25-32. DOI:10.2136/sssaj1983.03615995004700010005x
(  0) 0) |
| [22] |
Verhoef A, van den Hurk B J, Jacobs AF, et al. Thermal soil properties for vineyard (EFEDA-Ⅰ) and savanna(HAPEX-Sahel)sites . Agricultural and Forest Meteorology, 1996, 78(1): 1-18.
(  0) 0) |
| [23] |
Heusinkveld B, Jacobs A, Holtslag A, et al. Surface energy balance closure in an arid region: Role of soil heat flux . Agricultural and Forest Meteorology, 2004, 122(1): 21-37.
(  0) 0) |
| [24] |
董文杰, 汤懋苍. 用气象站地温资料计算多年平均土壤热流的初步结果. 高原气象, 1992, 11(2): 115-123. Dong W J, Tang M C. The preliminary results of calculating annual mean soil heat flux with temperature data (In Chinese). Plateau Meteorology, 1992, 11(2): 115-123. (  0) 0) |
| [25] |
王宝灵, 汤懋苍. 我国土壤热流计算结果的初步分析. 科学通报, 1993, 38(11): 1013-1016. Wang BL, Tang M C. Preliminary analysis on the results of the calculation of soil heat flux in China (In Chinese). Chinese Science Bulletin, 1993, 38(11): 1013-1016. (  0) 0) |
| [26] |
范新岗, 汤懋苍. 土壤传导-对流通量计算初步结果. 高原气象, 1994, 13(1): 14-19. Fan X G, Tang MC. A preliminary study on conductive and convective soil heat flux (In Chinese). Plateau Meteorology, 1994, 13(1): 14-19. (  0) 0) |
| [27] |
高志球, 卞林根, 张雅斌, 等. 土壤传导方程解析解和那曲地区土壤热扩散率研究. 气象学报, 2002, 60(3): 352-360. Gao Z Q, Bian L G, Zhang Y B, et al. Analytical solution of soil conduction equation and the study of soil thermal diffusivity in Naqu (In Chinese). Journal of Meteorological Research, 2002, 60(3): 352-360. DOI:10.11676/qxxb2002.042 (  0) 0) |
| [28] |
缪育聪, 刘树华, 吕世华, 等. 土壤热扩散率及其温度、热通量计算方法的比较研究. 地球物理学报, 2012, 55(2): 441-451. Miao Y C, Liu S H, Lü S H, et al. A comparative study of computing methods of soil thermal diffusivity, temperature and heat flux (In Chinese). Chinese Journal of Geophysics, 2012, 55(2): 441-451. (  0) 0) |
| [29] |
Miao JF, Chen D L, Borne K. Evaluation and comparison of noahand PleimXiu Land Surface models in MM5 using GÖTE2001 data: Spatial and temporal variations in near-surface air temperature . Journal of Applied Meteorology and climatology, 2007, 46(10): 1587-1605. DOI:10.1175/JAM2561.1
(  0) 0) |
| [30] |
de Silans A M BP, Monteny B A, Lhomme J P. Apparent soil thermal diffusivity, a case study:HAPEX-Sahel experiment . Agricultural and Forest Meteorology, 1996, 81(3/4): 201-216.
(  0) 0) |
| [31] |
Gao Z Q, Fan X G, Bian L G. An analytical solution to one-dimensional thermal conduction-convection in soil . Soil Science, 2003, 168(2): 99-106. DOI:10.1097/00010694-200302000-00004
(  0) 0) |
| [32] |
Gao Z Q. Determination of soil host flux in a Tibetan short-grass prairie . Boundary-Layer Meteorology, 2005, 114(1): 165-178. DOI:10.1007/s10546-004-8661-5
(  0) 0) |
| [33] |
Gao Z Q, Wang L L, Horton R. Comparison of six algorithms to determine the soil thermal diffusivity at a site in the Loess Plateau of China . Hydrology and Earth System Sciences, 2009, 6(2): 2247-2274. DOI:10.5194/hessd-6-2247-2009
(  0) 0) |
| [34] |
杨玮, 何金海, 王盘兴. 近42年来青藏高原年内降水时空不均匀性特征分析. 地理学报, 2011, 66(3): 376-384. Yang W, He J H, Wang P X. Inhomogeneity characteristics of intra-annual precipitation over the Tibetan Plateau in recent 42 years (In Chinese). Acta Geographica Sinica, 2011, 66(3): 376-384. DOI:10.11821/xb201103010 (  0) 0) |
| [35] |
张雯, 王磊, 陈权亮. 青藏高原东部土壤湿度变化及其与中国降水的关系. 成都信息工程学院学报, 2015, 30(1): 81-85. Zhang W, Wang L, Chen Q L. The soil moisture in eastern of Qinghai-Tibet Plateau and its relationship with precipitation in China (In Chinese). Journal of Chengdu University of Information Technology, 2015, 30(1): 81-85. (  0) 0) |
| [36] |
邵明安, 王全九, 黄明斌. 土壤物理学. 北京: 高等教育出版社, 2006, 170-175. Shao M A, Wang Q J, Huang M B. Soil physics (In Chinese). Beijing: Higher Education Press, 2006, 170-175. (  0) 0) |
| [37] |
Van WijkW R. Physics of plant environment . Amsterdam: North Holland Amsterdam Press, 1963, 1-156.
(  0) 0) |
| [38] |
李韧, 赵林, 丁永健, 等. 青藏高原北部不同下垫面土壤热力特性研究. 太阳能学报, 2013, 34(6): 1076-1084. Li R, Zhao L, Ding Y J, et al. Study on soil thermodynamic characteristics at different underlying surface in northern Qinghai-Tibetan Plateau (In Chinese). Acta Energiae Solaris Sinica, 2013, 34(6): 1076-1084. (  0) 0) |
| [39] |
Inaba H. Experimental study on the thermal properties of frozen soils . Cold Regions and Technology, 1983, 8(2): 181-187. DOI:10.1016/0165-232X(83)90008-3
(  0) 0) |
2. University of Chinese Academy of Sciences, Beijing 100049, China
 2018, Vol. 55
2018, Vol. 55


