2. 扬州工业职业技术学院,江苏扬州 225127;
3. 中国科学院大学,北京 100049
在生态学中,空间尺度通常指空间幅度和空间粒度。幅度是指区域空间范围大小,对土壤属性空间变异性特征研究具有明显影响作用[1-3]。粒度是指空间最小可辨识单元所代表的特征长度、面积或体积(如样方、像元),在地图学上表示为制图比例尺或栅格分辨率,即制图精度[4-6]。景观指数的粒度效应在土地利用类型方面已有很多研究,其中,部分学者定性地研究了景观指数随粒度变化的特征,结果表明,景观指数随粒度的增加呈上升或下降趋势[7-9]。也有学者基于不同比例尺讨论景观指数的粒度效应,并进行了矢量数据转换为栅格数据的适宜粒度研究,结果表明,景观指数随粒度的增大而增大或减小或无规则变化或基本不变,且适宜粒度随着比例尺的减小而增大[10-14]。
在土壤学领域,有学者将太湖地区不同比例尺土壤矢量数据分别转成不同分辨率的栅格数据,研究农田土壤碳库的指标变化,并以矢量数据获得的指标为基准,利用相对变异百分数(VIV)判别不同栅格数据与其对应比例尺土壤矢量数据之间的精度差异,在满足一定精度条件下得到栅格化的最佳表征粒度[15-16],并模拟土壤数据比例尺与栅格最佳分辨率转换对应关系[16]。陈粲等[17]利用江西省余江县1:5万土壤图,依据面积指标研究了在土类、亚类、土属和土种分类水平上土壤矢量图转化成不同大小栅格图过程中各类土壤分布的面积变化,得到不同土壤分类级别上土壤图栅格化的最佳粒度。但是研究中只选取了代表性土壤类型,而随着粒度的逐渐增大,细碎化的小面积土壤类型斑块逐渐消失,导致代表性的大面积土壤类型的栅格面积越来越大,所以仅仅依据面积一项指标,缺乏足够说服力。
20世纪80年代开展的全国第二次土壤普查工作,获得了海量的调查数据资料,土壤调查涉及全国2 444个县,312个国家农场和44个林场,土壤数据包括土壤形成、分类和分布,土壤类型和性质,土壤肥力,土壤资源和利用等,发表超过5 500份书面报告[18]。这些海量资料经过层层筛选、核准和编辑,也仅有少量数据得以在全国正式出版和发布,如中国1:100万土壤类型图,《中国土种志》等[18]。大量未得以正式出版发布的数据资料历经30多年,或沉睡、或丢失,即使有幸保存,但也因为缺乏数据说明信息、或说明信息不全、或者描述错误,而难以得到正确利用。对于那些未出版、数据说明又存在诸多问题的历史土壤类型图件,正确判断其制图精度,是利用这些珍贵数据资料的前提条件。因此,如何判断历史土壤类型图的制图精度,方法论问题是首先急需研究和解决的。
所以,本研究利用收集整理、标记为福建省1:25万土壤类型图的全国第二次土壤普查资料数据,尝试利用上述土壤景观格局指数的粒度效应原理及特征,构建土壤类型图的精度判断方法,并对该图制图精度进行定量化评估,为类似问题解决提供有效途径和方法,保护历史珍贵数据资料,并促进其得以正确利用。
1 材料与方法 1.1 研究区概况福建省处于中国东南沿海(115°50′~120°43′E,23°33′~28°19′N)(图 1),全省陆域面积12.14万 km2,属于亚热带海洋性季风气候,地势总体上西北高东南低,山地、丘陵占全省总面积的80%以上,土壤以红壤、砖红壤性红壤、水稻土、黄壤等为主[19]。

|
图 1 研究区位置及土壤类型分布图 Fig. 1 Location of the study area and soil type distribution map |
本研究收集整理标记为福建省1:25万土壤类型图的纸质图作为数据源。土壤类型包含土类、亚类、土属3个层次,在土属单元中还包含土壤质地和地形坡度等特征信息。其中,土壤质地特征分为粗粒质、中粒质、细粒质;地形坡度特征分为 < 5°、5°~20°、> 20°。本研究仅针对土壤发生分类的土壤类型信息。首先对纸质图进行扫描预处理,然后在ArcGIS 10.2的支持下进行地理配准、投影转换,再进行数字化、拓扑检查等,并根据不同土壤发生分类层次对原图进行重新编制,最后获得福建省土壤发生分类的土壤类型矢量数据。
1.3 矢量数据向栅格数据转换将矢量数据利用中心属性值法(Rule of Centric Cell,RCC)进行栅格化变换,即一个栅格单元的取值为该单元中心的类型属性值。由于不同土壤分类单元层次(土类、亚类、土属)本身各自代表不同土壤类型图的制图粒度,所以本研究对矢量土壤图进行了不同分类层次的栅格化,每种分类层次从30 m至8 km不等间距分别选取50个栅格粒度,用于土壤景观指数提取和粒度效应分析。
1.4 景观指数的选取及计算景观指数值是基于景观格局分析软件Fragstats 4.2计算的,30 m栅格粒度是省级幅度下软件可接受运算的最小栅格粒度。景观指数包括斑块水平、斑块类型水平和景观水平3种类型。其中,前两种类型指数是针对单个斑块或不同类型斑块进行分析,而景观水平指数则是对研究区域内整体特征的描述。选取景观指数时,依据前人研究[10, 20],且兼顾各种粒度效应的同时,尽量避开具有相关性的指数,使之能全面反映研究区土壤类型景观指数的粒度效应。本文针对面积/密度/边长、形状、聚集/分布、连接性和多样性等方面,在景观水平上选取总面积(TA)、总边缘长度(TE)、景观形状指数(LSI)、最大斑块指数(LPI)、斑块面积标准差(AREA_SD)、周长面积分维数(PAFRAC)、聚合度(AI)、景观分离度(DIVISION)、分散指数(SPLIT)、有效网格大小(MESH)、斑块内聚力指数(COHESION)、斑块丰富度(PR)、斑块丰富度密度(PRD)、香农多样性指数(SHDI)、香农均匀度指数(SHEI)15个景观格局指数,探讨不同分类级别土壤类型景观指数的粒度效应。各指数的公式和含义参考相关文献[21]。
1.5 不同土壤分类粒度量化及制图精度判断在研究景观指数对不同粒度响应的过程中,用指标相对变异百分数(VIV)来反映由矢量图斑单元转成不同粒度栅格单元时景观指数的变化情况。研究显示,1:5万土壤类型矢量图的最佳表征粒度大于100 m×100 m [17, 22],表明以该粒度进行矢量数据的栅格化变换,其栅格数据精度可等同于原矢量数据。本研究土壤类型矢量图比例尺标记1:25万,最佳表征粒度应远大于100 m×100 m,粒度为30 m×30 m栅格数据精度应等同于原矢量数据。因此,本研究以粒度30 m×30 m对应的景观指数为基准数据,不同粒度对应的景观指数相对于基准数据进行比较。其中相对变异百分数(VIV)表示如下:
| $ {\rm{VIV}} = \frac{{{\rm{IV}}\left( {\rm{A}} \right) - {\rm{IV}}\left( {\rm{B}} \right)}}{{{\rm{IV}}\left( {\rm{A}} \right)}} \times 100\% $ | (1) |
式中,IV(A)为粒度30 m×30 m对应的指标值,IV(B)为不同粒度对应的指标值。
当所有指标|VIV| < 1%,且栅格单元粒度达到最大时,则认为该粒度为土壤分类粒度的最佳表征粒度[23]。最后依据土壤图比例尺与最佳表征粒度的函数关系,判定土壤制图精度[22]。统计分析利用Origin 8.5进行。
2 结果与讨论 2.1 土壤矢量图件基本信息统计特征矢量图件基本信息统计结果表明,该图有11个土类,23个亚类,55个土属,基本制图单元为土属。共有2 189个图斑,面积为12.24万 km2,图斑密度为每平方公里0.017 9个。而已经出版的福建省1:50万、1:100万和1:400万土壤类型图的矢量化图斑数分别为11 855个、3 412个、263个,面积分别为12.37万 km2、12.35万 km2、12.17万 km2,图斑密度依次为每平方公里0.095 8个、0.027 6个、0.002 2个,基本制图单元分别为土属、亚类、土类[24]。从图件基本信息可初步判断,该土壤矢量图的制图精度(粒度)应处于1:50万和1:400万之间。
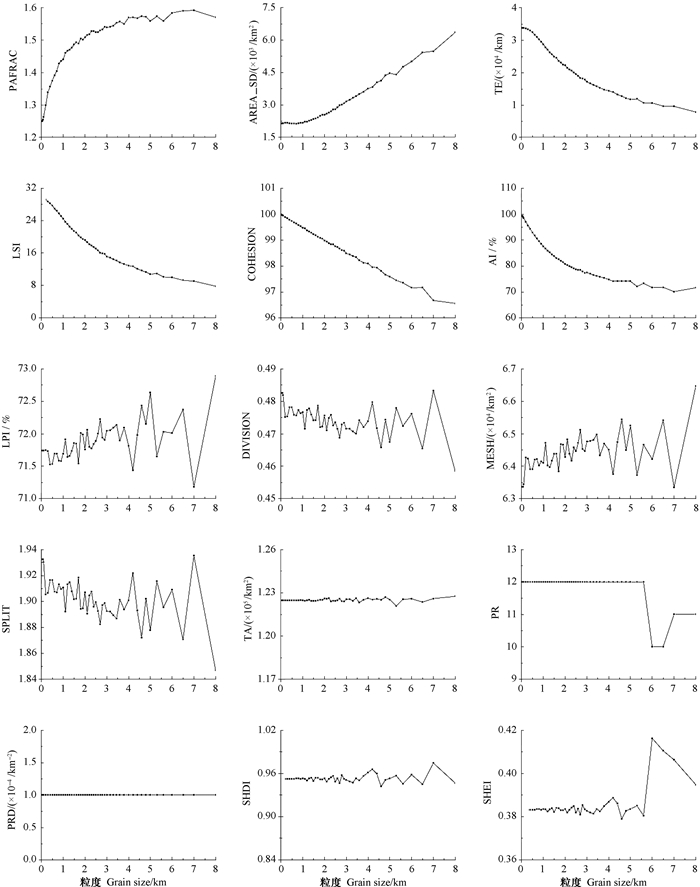
2.2 土壤景观指数的粒度效应特征研究表明,随着粒度的增大,各景观指数呈现出不同的变化趋势,景观指数具有明显的粒度效应(图 2、图 3和图 4)。不同土壤分类层次相同的景观指数具有相同的变化趋势。依据各景观指数随粒度的增大所呈现的变化趋势,可以将景观指数的粒度效应划分为以下4类:(1)景观指数随粒度增加呈现出增加的变化趋势,包括PAFRAC和AREA_SD。随着粒度的增加,PAFRAC呈对数函数上升,说明景观形状变化较大,复杂性增强;AREA_SD随着粒度的增加呈线性上升。(2)景观指数随着粒度增加呈现出减小的变化趋势,包括TE、LSI、COHESION和AI。(3)景观指数随着粒度增加呈现出不稳定无规律性变化趋势,包括LPI、DIVISION、MESH和SPLIT,粒度效应较为复杂。(4)随着粒度增加呈现出稳定或先稳定再变动的趋势,包括TA、PR、PRD、SHDI和SHEI。其中,土类和亚类的PRD在分析粒度范围内的变化不明显,其余各指数呈现出先稳定后变动的趋势。
|
注:TA、TE、LSI、LPI、AREA_SD、PAFRAC、AI、DIVISION、SPLIT、MESH、COHESION、PRD、PR、SHDI、SHEI分别代表总面积、总边缘长度、景观形状指数、最大斑块指数、斑块面积标准差、周长面积分维数、聚合度、景观分离度、分散指数、有效网格大小、斑块内聚力指数、斑块丰富度、斑块丰富度密度、香农多样性指数和香农均匀度指数 Note: TA, TE, LSI, LPI, AREA_SD, PAFRAC, AI, DIVISION, SPLIT, MESH, COHESION, PRD, PR, SHDI and SHEI represent total area, total edge length, landscape shape index, largest patch index, standard deviation of patch area, perimeter-area fractal dimension, aggregation index, patch cohesion index, landscape division index, splitting index, effective mesh size, patch richness, patch richness density, shannon diversity index and shannon evenness index, respectively 图 2 土类各景观指数粒度效应图 Fig. 2 Metrics of grain-size dependence of landscape indices at the soil great group level |
|
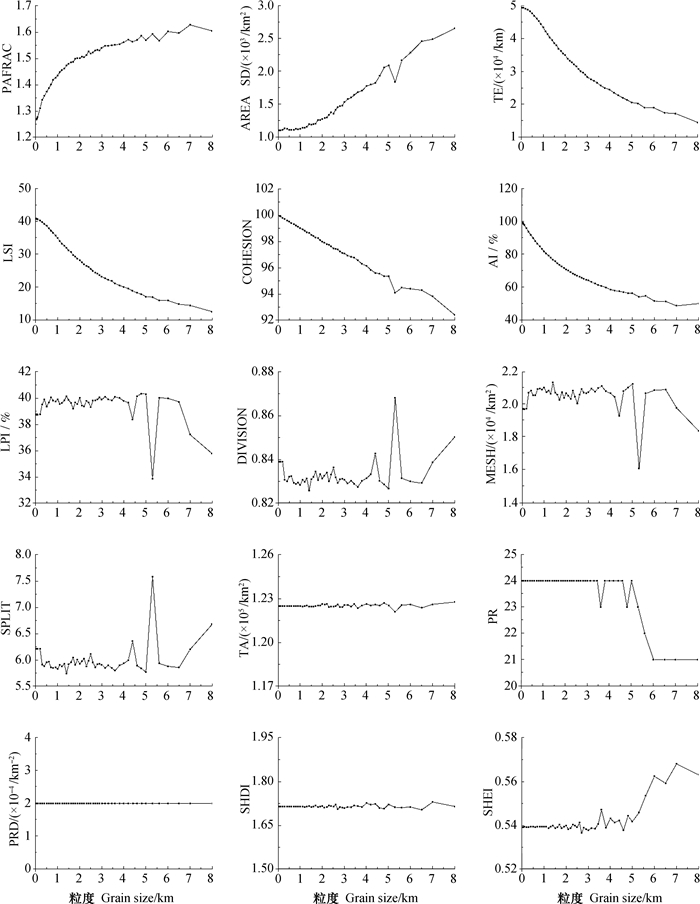
图 3 亚类各景观指数粒度效应图 Fig. 3 Metrics of grain-size dependence of landscape indices at the soil subgroup level |
|
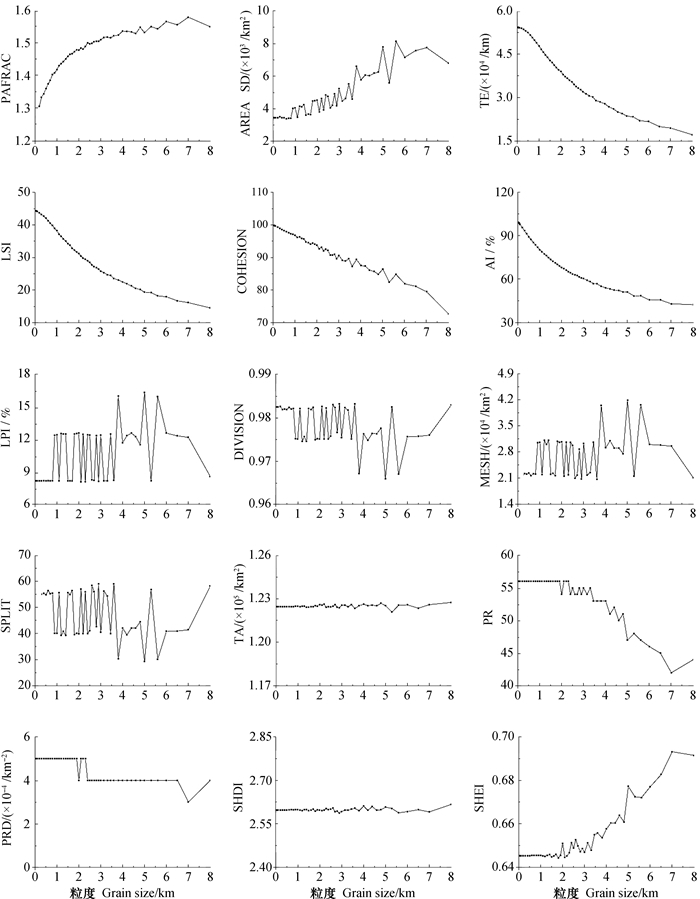
图 4 土属各景观指数粒度效应图 Fig. 4 Metrics of grain-size dependence of landscape indices at the soil family level |
陈粲等[17]研究显示TA随粒度的增加呈现出先稳定后波动的趋势,吴未等[25]、张庆印和樊军[26]研究表明LSI和COHESION总体呈现下降的趋势,这些均与本文结果具有一致性。Wu等[27]发现SHDI随粒度增加呈阶梯下降趋势,张庆印和樊军[26]研究得出在60 m内PR、SHDI和SHEI随粒度的增加基本无变化,邱扬等[11]和包宇[14]研究表明SHDI和SHEI先小幅波动后大幅度波动,而本研究结果显示出了并不完全相同的结果,SHDI和SHEI随粒度的增加呈现先稳定再变动的趋势。游丽平等[28]研究表明,PAFRAC随粒度增大而减小,与本文研究结果相反。显然,已有景观指数的粒度效应研究结果与本研究并不完全一致,这是因为已有研究中所选粒度范围、空间数据聚合方式、景观类型多少以及景观格局指数本身算法等不同,均可能造成分析结果的差异。
2.3 不同土壤分类层次的最佳表征粒度本研究选取15种景观指数分析其粒度效应,最终选取的土壤图评价指标是要能够求得土壤矢量图栅格化的最佳表征粒度,根据最佳表征粒度推断土壤类型图的比例尺,定量化评估其制图精度。而采用不同栅格粒度进行数据变换,会使得数据信息的损失程度和冗余程度产生差异,进而影响景观格局分析的准确性[29]和分析效率[30]。因此,需要寻找适宜粒度,使得栅格数据既能最大限度保持数据精度又能降低数据冗余度[31],而该粒度即为土壤矢量图栅格化的最佳表征粒度。若景观指数随粒度增加出现先稳定不变后波动的趋势,那么在稳定不变的粒度区域所对应的栅格数据与原始矢量数据具有相同的精度,在此基础上设定在一定数据精度范围内(|VIV| < 1%)所对应的最大栅格粒度为最佳表征粒度[23]。而若景观指数随着粒度增加一直处于变化状态,表明栅格数据的精度始终处于损失状态,此时求算最佳表征粒度无意义。最终,在不同土壤分类层次上,分别有5个景观格局指数TA、PR、PRD、SHDI、SHEI随着粒度增加呈现稳定或先稳定再变动的变化趋势。
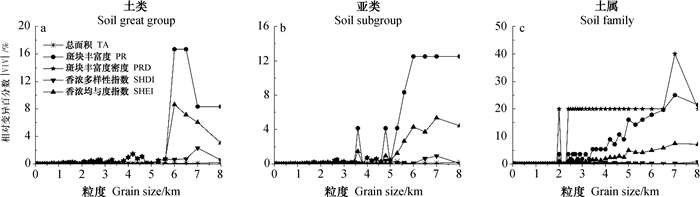
在土类层次上,TA、PR、SHDI和SHEI的|VIV|总体上均呈现出先稳定后变动的趋势,而PRD的|VIV|在分析粒度范围内的变化不明显(图 5a)。当粒度≤ 4.00 km时,各指标的|VIV| < 1%;当粒度为4.20 km时,SHDI和SHEI的|VIV| > 1%;当粒度为6.00 km时,PR的|VIV| > 1%;TA和PRD的|VIV|在本研究粒度下均小于1%。所以,土类层次上矢量数据栅格化的最佳表征粒度为4.00 km。
|
图 5 不同土壤分类层次景观指数相对变异系数(VIV)图 Fig. 5 VIV of landscape indices relative to soil taxonomical hierarchy |
在亚类层次上,PRD的|VIV|变化不明显,其余指标的|VIV|呈现出先稳定后波动的趋势(图 5b)。当粒度≤3.45 km时,各指标的|VIV| < 1%;当粒度为3.60 km时,PR和SHEI的|VIV| > 1%;而TA、PRD和SHDI的|VIV|在本研究粒度下均小于1%。因此,亚类层次矢量数据栅格化的最佳表征粒度为3.45 km。
在土属层次上,除PRD的|VIV|的变化不太明显外,其余各指标的|VIV|均呈现出先稳定后波动的趋势(图 5c)。当粒度≤1.90 km时,各指标的|VIV| < 1%;当粒度为2.00 km时,PR和PRD的指标|VIV| > 1%;当粒度为2.60 km时,SHEI的|VIV| > 1%;TA和SHDI的|VIV|在本研究粒度下均小于1%。可以认为,土属层次矢量数据栅格化的最佳表征粒度为1.90 km。
2.4 土壤图的制图精度本研究区地形以山地丘陵为主,由于地形比较破碎,导致其空间异质性较大,而Yu等[22]研究的太湖地区虽然以平原为主,但河网密布,城镇分布密集,土地利用类型的变异性及不连续性不亚于本文研究区的空间异质性。由此推测,太湖地区的土壤数据比例尺与栅格分辨率等精度转换关系y =-0.80×10-6x2 + 0.022 8x + 0.021 1(R2 = 0.999 4,P < 0.05)[22]同样也应该适用于本研究区。因此,依据土壤图最佳表征粒度与制图比例尺的函数关系[22]和土类、亚类、土属的最佳表征粒度4.00 km、3.45 km、1.90 km,则可判断出相应制图比例尺分别为1:180万、1:160万、1:85万。虽然所得矢量图比例尺与原始比例尺1:25万相差很多,但也符合土壤矢量图件信息的初步判断。
该土壤类型图除分别为土类、亚类、土属等土壤发生分类层次信息外,在土属分类层次单元中还包含土壤质地和地形坡度信息,而本研究仅针对土壤发生分类的类型信息,这是导致所得比例尺较原始比例尺小得多的主要原因。在土壤图制图规范中,1:25万土壤图的基本制图单元为土属或土种,1:50万的基本制图单元为土属[16],1:100万土壤图在平原区的基本制图单元为土属,山区的基本制图单元为亚类[32],1:400万的基本制图单元为土类[33]。所以,在土类层次上,本研究所用土壤图数据精度高于1:400万,低于1:100万;在亚类层次上,数据精度小于1:100万;在土属层次上,数据精度低于1:50万,高于1:100万。因此,对于那些未出版、数据说明又存在诸多问题的历史土壤类型图件,正确判断其制图精度是非常必要的。
3 结论本文利用收集整理的、标记为福建省1:25万土壤类型图,分析其在栅格数据下不同土壤分类层次景观指数的粒度效应,以粒度30 m×30 m对应的景观指数为基准,不同粒度对应的景观指数与基准数据比较,设定相对变异百分数|VIV| < 1%时所对应的最大粒度为土壤矢量图栅格化的最佳表征粒度,并以此推断土壤类型图的比例尺,判定其制图精度,实现了历史土壤图件精度的定量化准确评估。案例研究结果显示,收集整理的、标记为福建省1:25万土壤图,在土类、亚类、土属水平的实际制图精度分别仅为比例尺1:180万、1:160万、1:85万,两者差别显著。本研究为判断历史土壤类型图的制图精度提供了有效途径和方法,对于历史珍贵数据资料的正确利用具有重要意义。
| [1] |
王丹丹, 岳书平, 林芬芳, 等. 东北地区旱地土壤全氮空间变异性对幅度拓展的响应. 土壤学报, 2012, 49(4): 625-635. Wang D D, Yue S P, Lin F F, et al. Response of spatial variability of soil total nitrogen to expansion of uplands in scale in Northeast China (In Chinese). Acta Pedologica Sinica, 2012, 49(4): 625-635. (  0) 0) |
| [2] |
Zhang Z Q, Yu D S, Shi X Z, et al. Priority selection rating of sampling density and interpolation method for detecting the spatial variability of soil organic carbon in China . Environmental Earth Sciences, 2015, 73(5): 2287-2297. DOI:10.1007/s12665-014-3580-3
(  0) 0) |
| [3] |
王秀虹, 于东升, 潘月, 等. 单种复合类型单元土壤全量元素空间变异的幅度效应. 土壤学报, 2017, 54(4): 864-873. Wang X H, Yu D S, Pan Y, et al. Scale effect on spatial variability of soil total elements in single complex type unit of land use-soil type (In Chinese). Acta Pedologica Sinica, 2017, 54(4): 864-873. (  0) 0) |
| [4] |
Lam N S N, Quattrochi D A. On the issues of scale, resolution, and fractal analysis in the mapping sciences . Professional Geographer, 1992, 144: 88-98.
(  0) 0) |
| [5] |
Jenerette G D, Wu J G. On the definitions of scale . Bulletin of the Ecological Society of America, 2000, 81: 104-105.
(  0) 0) |
| [6] |
邬建国. 景观生态学:格局、过程、尺度与等级. 第2版. 北京: 高等教育出版社, 2000. Wu J G. Landscape ecology-pattern, process, scale and hierarchy (In Chinese). 2nd ed. Beijing: Higher Education Press, 2000. (  0) 0) |
| [7] |
Qi Y, Wu J G. Effects of changing spatial resolution on the results of landscape pattern analysis using spatial autocorrelation indices . Landscape Ecology, 1996, 11(1): 39-49. DOI:10.1007/BF02087112
(  0) 0) |
| [8] |
Wu J G. Effects of changing scale on landscape pattern analysis:Scaling relations . Landscape Ecology, 2004, 19(2): 125-138. DOI:10.1023/B:LAND.0000021711.40074.ae
(  0) 0) |
| [9] |
陈永林, 谢炳庚, 李晓青. 长沙市土地利用格局变化的空间粒度效应. 地理科学, 2016, 36(4): 564-570. Chen Y L, Xie B G, Li X Q. Spatial grain size effect on land use pattern changes in Changsha City (In Chinese). Scientia Geographica Sinica, 2016, 36(4): 564-570. (  0) 0) |
| [10] |
赵文武, 傅伯杰, 陈利顶. 景观指数的粒度变化效应. 第四纪研究, 2003, 23(3): 326-333. Zhao W W, Fu B J, Chen L D. The effects of grain change on landscape indices (In Chinese). Quaternary Sciences, 2003, 23(3): 326-333. DOI:10.3321/j.issn:1001-7410.2003.03.011 (  0) 0) |
| [11] |
邱扬, 杨磊, 王军, 等. 黄土丘陵小流域景观格局指数的粒度效应. 应用生态学报, 2010, 21(5): 1159-1166. Qiu Y, Yang L, Wang J, et al. Grain effect of landscape pattern indices in a gully catchment of Loess Plateau, China (In Chinese). Chinese Journal of Applied Ecology, 2010, 21(5): 1159-1166. (  0) 0) |
| [12] |
朱开群. 土地整理项目区景观粒度效应与景观格局分析. 南京: 南京大学, 2011. Zhu K Q. The landscape grain size effect and landscape pattern analysis for land consolidation district (In Chinese). Nanjing: Nanjing University, 2011. (  0) 0) |
| [13] |
郭冠华, 陈颖彪, 魏建兵, 等. 粒度变化对城市热岛空间格局分析的影响. 生态学报, 2012, 32(12): 3764-3772. Guo G H, Chen Y B, Wei J B, et al. Impacts of grid sizes on urban heat island pattern analysis (In Chinese). Acta Ecologica Sinica, 2012, 32(12): 3764-3772. (  0) 0) |
| [14] |
包宇. 深圳市景观指数的粒度效应分析及指数时空动态研究. 武汉: 武汉大学, 2017. Bao Y. Particle size effect analysis and index temporal and spatial dynamics of landscape index in Shenzhen City (In Chinese). Wuhan: Wuhan University, 2017. (  0) 0) |
| [15] |
Yu D S, Yang H, Shi X Z, et al. Effects of soil spatial resolution on quantifying CH4 and N2O emissions from rice fields in the Tai Lake region of China by DNDC model . Global Biogeochemical Cycles, 2010, 25(2): 1-8.
(  0) 0) |
| [16] |
Yu D S, Ni Y L, Shi X Z, et al. Optimal soil raster unit resolutions in estimation of soil organic carbon pool at different map scales . Soil Science Society of America Journal, 2014, 78(3): 1079-1086. DOI:10.2136/sssaj2013.07.0262
(  0) 0) |
| [17] |
陈粲, 张忠启, 史学正, 等. 不同分类级别土壤矢量图与最小可分栅格的关系研究. 土壤学报, 2011, 48(3): 470-478. Chen C, Zhang Z Q, Shi X Z, et al. Relationship of soil vector maps of different classification grades and the smallest dividable raster (In Chinese). Acta Pedologica Sinica, 2011, 48(3): 470-478. (  0) 0) |
| [18] |
Shi X Z, Yu D S, Warner E D, et al. Soil database of 1:1000000 digital soil survey and reference system of the Chinese genetic soil classification system . Soil Survery Horizons, 2004, 45(4): 129-136. DOI:10.2136/sh2004.4.0129
(  0) 0) |
| [19] |
福建土壤普查办公室. 福建土壤. 福州: 福建科技出版社, 1991. Fujian Soil Survey Office. Fujian soil (In Chinese). Fuzhou: FujianScience and Technology Press, 1991. (  0) 0) |
| [20] |
布仁仓, 胡远满, 常禹, 等. 景观指数之间的相关分析. 生态学报, 2005, 25(10): 2764-2775. Bu R C, Hu Y M, Chang Y, et al. A correlation analysis on landscape metrics (In Chinese). Acta Ecologica Sinica, 2005, 25(10): 2764-2775. DOI:10.3321/j.issn:1000-0933.2005.10.044 (  0) 0) |
| [21] |
Mcgarigal K S, Cushman S A, Neel M C, et al.Fragstats: Spatial pattern analysis program for categorical maps.Analysis 3.3.2002
(  0) 0) |
| [22] |
Yu D S, Pan Y, Zhang H D, et al. Equality testing for soil grid unit resolutions to polygon unit scales with DNDC modeling of regional SOC pools . Chinese Geographical Science, 2017, 27(4): 552-568. DOI:10.1007/s11769-017-0887-5
(  0) 0) |
| [23] |
Whitmore A P, Klein-Gunnewiek H, Crocker G J, et al. Simulating trends in soil organic carbon in long-term experiments using the Verbeme/MOTOR model . Geoderma, 1997, 81(1): 137-151.
(  0) 0) |
| [24] |
史学正, 于东升, 高鹏, 等. 中国土壤信息系统(SISChina)及其应用基础研究. 土壤, 2007, 39(3): 329-333. Shi X Z, Yu D S, Gao P, et al. Soil information system of China (SISChina) and its application (In Chinese). Soils, 2007, 39(3): 329-333. DOI:10.3321/j.issn:0253-9829.2007.03.001 (  0) 0) |
| [25] |
吴未, 范诗薇, 许丽萍, 等. 无锡市景观指数的粒度效应研究. 自然资源学报, 2016, 31(3): 413-424. Wu W, Fan S W, Xu L P, et al. Grain size effect of landscape metrics in Wuxi City (In Chinese). Journal of Natural Resources, 2016, 31(3): 413-424. (  0) 0) |
| [26] |
张庆印, 樊军. 高精度遥感影像下农牧交错带小流域景观特征的粒度效应. 生态学报, 2013, 33(24): 7739-7747. Zhang Q Y, Fan J. Effects of higher resolution image and spatial grain size on landscape pattern in a small watershed of the farming-pastoral zone (In Chinese). Acta Ecologica Sinica, 2013, 33(24): 7739-7747. (  0) 0) |
| [27] |
Wu J G, Shen W J, Sun W Z, et al. Empirical patterns of the effects of changing scale on landscape metrics . Landscape Ecology, 2002, 17(8): 761-782. DOI:10.1023/A:1022995922992
(  0) 0) |
| [28] |
游丽平, 林广发, 杨陈照, 等. 景观指数的空间尺度效应分析-以厦门岛土地利用格局为例. 地球信息科学, 2008, 10(1): 74-79. You L P, Lin G F, Yang C Z, et al. The effects of spatial scales on landscape indices-A case study of the landuse pattern of Xiamen Island (In Chinese). Geo-Information Science, 2008, 10(1): 74-79. DOI:10.3969/j.issn.1560-8999.2008.01.013 (  0) 0) |
| [29] |
余新晓, 牛健植, 关文彬, 等. 景观生态学. 北京: 高等教育出版社, 2006. Yu X X, Niu J Z, Guan W B, et al. Landscape ecology (In Chinese). Beijing: Higher Education Press, 2006. (  0) 0) |
| [30] |
Carver S J, Brunsdon C F. Vector to raster conversion error and feature complexity:An empirical study using simulated data . International Journal of Geographical Information Systems, 1994, 8(3): 261-270. DOI:10.1080/02693799408901999
(  0) 0) |
| [31] |
倪元龙, 于东升, 张黎明, 等. 不同比例尺农田土壤碳库模拟的最佳栅格单元分辨率. 土壤学报, 2014, 51(1): 32-40. Ni Y L, Yu D S, Zhang L M, et al. Optimal resolution of grid units of simulated paddy soil organic carbon pools of various scales (In Chinese). Acta Pedologica Sinica, 2014, 51(1): 32-40. (  0) 0) |
| [32] |
李锦, 曹锦铎, 王鹤林. 中国1:100万土壤图制图原则和方法的研究. 土壤, 1986, 18(1): 8-14. Li J, Cao J D, Wang H L. Studies on the principles and methods of soil map mapping at 1:1000000 of China (In Chinese). Soils, 1986, 18(1): 8-14. (  0) 0) |
| [33] |
李锦, 周明枞. 1:400万中华人民共和国土壤图. 中国科学院地学情报网网讯, 1986(Z1): 97-98. Li J, Zhou M Z. 1:4000000 soil map of the People's Republic of China (In Chinese). Chinese Academy of Sciences Earth Science Information Network News, 1986(Z1): 97-98. (  0) 0) |
2. Yangzhou Polytechnic Institute, Yangzhou, Jiangsu 225127, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
 2019, Vol. 56
2019, Vol. 56


