紫色土地区广泛分布着坡耕地,坡面在集中水流冲刷下极易造成水土流失,紫色土区降雨充沛,在低洼地区易形成饱和状态,相关研究[1-2]表明,饱和土在细沟土壤抗蚀性、产流产沙方面与非饱和土存在差异。由于紫色土具有岩土二元结构[3],当雨水渗至耕层与土壤下伏母质交界的弱透水层时,入渗性能降低,土壤的黏结性、孔隙水压力等土壤性质发生显著变化,导致土壤抗蚀性与其他土壤类型产生差异。细沟径流流速作为基本的水动力学参数之一,其测量大多采用染色剂示踪法[4],而染色剂示踪法测得的流速为水流的表层流速,需乘以相应的修正系数才能得到细沟的平均流速[5]。Lei等[6-7]提出电解质脉冲边界模型法及其改进方法对细沟流速进行测量,电解质脉冲边界模型法无需对径流流速进行校正,且在一定条件下可准确测定水流真实流速,因此发展了相应的测量仪器系统。
细沟侵蚀是坡面侵蚀的重要方式,对于坡面细沟侵蚀的水力学特征,相关研究主要分为以下几个阶段进行:从坡面开始侵蚀到细沟发育的完整过程[8],坡面流和细沟流的对比[9],以及跌坎、细沟产生的临界条件[10],上述研究表明坡面侵蚀过程具有明显的阶段性[11]。由于自然条件下存在间歇性降雨,会出现前期已经发育成型的细沟经历二次降雨的情况,因此发育平稳的细沟流水力学特征还需进一步研究。在水力学特征研究中,一方面,关于流量和坡度对流速的影响,许多试验通过改变流量和坡度范围、供试土壤和侵蚀方式,获得更全面的拟合方程[12-13]。另一方面,关于不同细沟侵蚀阶段的研究,大多仅限于细沟流速的对比[14-15],事实上,除了流速,探究其他水力参数的变化规律同等重要,许多学者在测量径流流速的基础上对雷诺数(Re)、弗劳德数(Fr)、达西阻力系数(f)和曼宁糙率系数(n)等一系列水力学参数进行计算[16],以明确相应试验条件下的水流流态及阻力特征。然而,在这些研究中,不同细沟侵蚀阶段对各水力参数的影响尚缺乏系统分析,从而更准确地定义细沟流水力特征。
基于此,本试验以电解质脉冲边界模型法测定的细沟流速为基础,通过不同流量、坡度的人工模拟冲刷试验,对饱和紫色土初始态和稳定态细沟水力学特征进行对比分析,从而揭示细沟不同发育阶段的水力学特征,以期为土壤侵蚀物理模型的建立提供理论依据。
1 材料与方法 1.1 试验材料及试验设计于2018年7月在中国农业大学水利试验大厅进行试验,试验装置由变坡土槽、饱和供水装置和流速测量系统组成。试验使用长8 m、宽1 m、高30 cm,坡度可在0~20°之间调节的钢制土槽,用钢板将土槽改造成9条长、宽分别为8 m、0.1 m的限定性细沟[17],在土槽的左侧有用于设置饱和土壤的供水装置。供试土壤为紫色土,于2018年6月取自重庆市北碚区(106°25′27″E,29°48′40″N),试验前去除土壤中石块、草根,并进行破碎处理,风干后过10 mm筛。土壤容重为1.28 g·cm–3,初始土壤含水率为3%,饱和导水率为16.61×10–3 cm·min–1,粒径组成采用马尔文激光粒度仪测定,如表 1所示。
|
|
表 1 供试土样粒径组成 Table 1 Soil Particle composition of the experimental soil |
本试验设计放水冲刷流量为2、4、8 L·min–1[18],土槽坡度为5°、10°、15°、20°,每个组合设3次重复,在相邻的3条细沟中分别进行冲刷视为同一工况下的3次重复,每条沟冲刷2次,分别为初始态细沟和稳定态细沟,改变流量(2、4、8 L·min–1),重复试验,再改变坡度(5°、10°、15°、20°)进行相应的试验。细沟侵蚀阶段分为初始态和稳定态细沟侵蚀阶段[14](图 1),从冲刷开始计时,形成稳定态细沟所需时间为4~5 min。初始态细沟是指在第一次测量流速时细沟坡面还未经历水流冲刷,为未开始发育的限定性细沟;稳定态细沟是指已经较为充分发育的限定性细沟,具有相对稳定的形态。

|
注:a)初始态细沟RN;b)稳定态细沟RE。Note:a)Non-eroded rill;b)Eroding rill. 图 1 细沟侵蚀不同阶段 Fig. 1 Different erosion states of the rills |
试验土装填及供水方法:为布设土壤饱和底部供水装置,沿顺坡方向将每条限定性细沟分成8段,每段长1 m,再将每段分为0.1 m和0.9 m两个单元。在每个0.1 m单元中部,用直径为10 mm的PVC渗流管供水,每条PVC渗流管上均匀钻有3个直径2 mm的渗水孔,水流通过供水竖管将水源转移至每个溢流管中,由溢流管将水供应到每条细沟中(图 2a),且渗流管均用透水性良好的土工织物包裹以防止土壤颗粒进入渗水孔阻塞[14]。0.1 m单元在土槽底部与下管壁之间填入黏土并压实,该层之上铺设纱布,在黏土上方填入直径为0.5 cm的碎石至5 cm厚,0.9 m单元不做处理,直接填入5 cm厚的黏土。控制两个单元的黏土层部分容重为1.5 g·cm–3,用以模拟犁底层[19]。实验前将土样装填20 cm的深度以模拟耕作层,分4层装填并逐层打毛,填土容重控制在1.3 g·cm–3。其他沟段用相同的方式处理。将供水竖管调至与土面平行的位置,采用极小的流量将水流供入碎石层,再由碎石层从土壤底部开始供水直至饱和,根据土壤饱和导水率计算得到达到饱和所需的时间约为15.67 h。为尽量减小钢板边壁对水流及侵蚀过程的影响,对水槽钢板和地表进行处理:在钢板上粘上与供试土壤相同的土粒,使其尽可能接近试验土同样的糙度,且为了让水流(细沟)处于水槽的中间以尽可能降低钢板壁(沟壁)对水流的影响,地表做成略带“V”形。
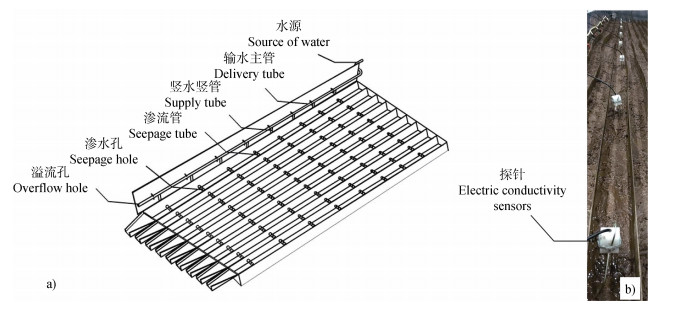
|
注:a)土槽及饱和装置示意图;b)流速测量装置实物图。Note:a)Sketch of the soil flume and saturation device,and b)Flow velocity measuring device. 图 2 试验装置图 Fig. 2 Device used in the flume scouring experiment |
流速测量方法:流速测定采用电解质脉冲边界模型法[7],流速测量系统由操作控制计算机、数据采集管理器、感应探针和盐溶液注入装置组成。在水槽前端固定盐溶液注入装置,在细沟入口前缘铺设海绵层,避免水流在入口处直接集中冲刷土壤表面,在距水槽末端10 cm,1、2、3、4、5、6、7、8 m各固定1根探针,共9根探针,用以感应水流电导信号(图 2b)。仪器调试完成后,从细沟入口处将氯化钾饱和溶液滴入水流,计算机中装有的软件自动完成记录和计算。根据董月群等[20]的试验结果,在采用电解质脉冲边界模型法测量流速的过程中,只有当测量距离达到一定时才能准确测定流速值。为此,在固定的9根探针中,仅采用3~8 m处探针测得的流速数据[21],将这6个不同坡长处的流速值平均即可得到相应工况下的径流流速。
1.3 相关参数的计算方法由于整个试验过程全部是细沟侵蚀阶段,断面形态复杂多变,直接测量误差较大,本试验根据细沟水流连续性方程,将细沟过水断面近似为矩形,且细沟平均径流深(h)一般只有几厘米,不会带来很大误差,表达式为:
| $ h = \frac{Q}{{V{\rm{\cdot}}b}} $ | (1) |
式中,Q为细沟流量,m3·s–1;V为流速,m·s–1;b为细沟宽度,取0.1 m[19]。
雷诺数(Re)表征水流惯性力与黏性力的比值的无量纲参数。弗劳德数(Fr)也是判断水流运动状况的无量纲参数之一,反映水流的惯性力与重力之比。表达式为:
| $ Re = \frac{{V\cdot h}}{v} $ | (2) |
| $ Fr = \frac{V}{{\sqrt {g\cdot h} }} $ | (3) |
式中,
达西阻力系数(f)和曼宁糙率系数(n)可直接反映出细沟径流沿坡面运动时所受阻力大小。表达式为:
| $ f = \frac{{8\cdot g\cdot h\cdot J}}{{{V^2}}} $ | (4) |
| $ n = \frac{{{R^{2/3}}\cdot{J^{1/2}}}}{V} $ | (5) |
式中,J为水力坡度,由于试验坡长较长,可取J=sinθ(θ为水槽坡度),无量纲。
1.4 数据处理多重比较采用LSD最小显著差数法(P < 0.05),不同字母(a和b)表征相同坡度下的流量处理在P < 0.05时差异显著。各水力学参数采用下标N表征初始态细沟,下标E表征稳定态细沟。本文各项散点拟合图采用Origin 9.0软件绘制,统计分析采用SPSS 23.0软件完成。
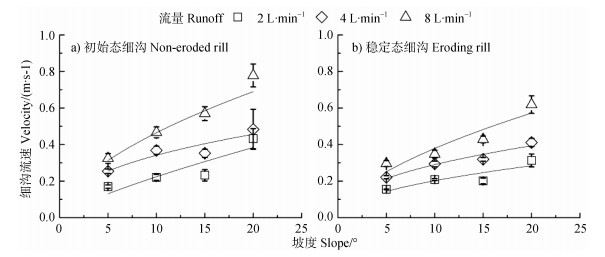
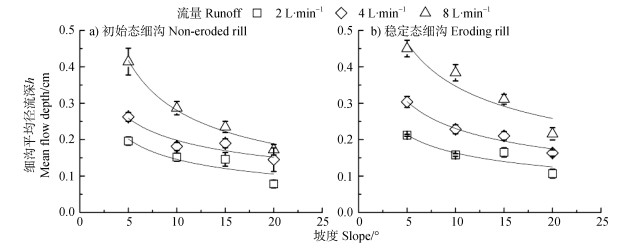
2 结果 2.1 流速和平均径流深流速(V)和平均径流深(h)是研究细沟径流最基础的水力学参数。初始态和稳定态细沟流速和随坡度变化的关系曲线如图 3所示,平均径流深随坡度变化的关系曲线如图 4所示。在不同细沟侵蚀阶段,初始态细沟流速VN介于0.170~0.778 m·s–1之间(图 3),初始态细沟流速在坡度为20°时稳定性较差,在其他工况下重现性较好,是因为随着坡度越来越大,细沟发育愈发剧烈,更容易形成复杂的微地貌,稳定态细沟流速VE介于0.156~0.619 m·s–1之间(图 4)。初始态细沟平均径流深hN介于0.078~0.413 cm之间,稳定态细沟平均径流深hE介于0.107~0.450 cm之间。在同一流量和坡度工况下,初始态流速VN>稳定态细沟VE,初始态平均径流深hN<稳定态平均径流深hE。
|
图 3 初始态(a)和稳定态(b)细沟流速与坡度间关系曲线 Fig. 3 Relationship curve between flow velocity and slope gradient relative to state of the rill |
|
注:误差棒表示3个重复的标准差。 Note:Error bars indicate the standard deviation of 3 replicates(n=3). 图 4 初始态(a)和稳定态(b)细沟平均径流深与坡度间关系曲线 Fig. 4 Relationship curve between mean flow depth and slope gradient relative to state of the rill |
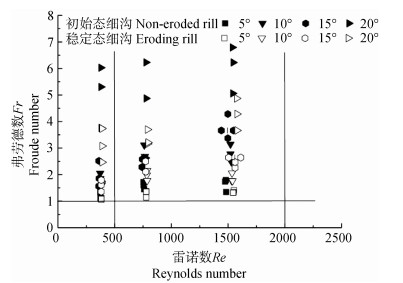
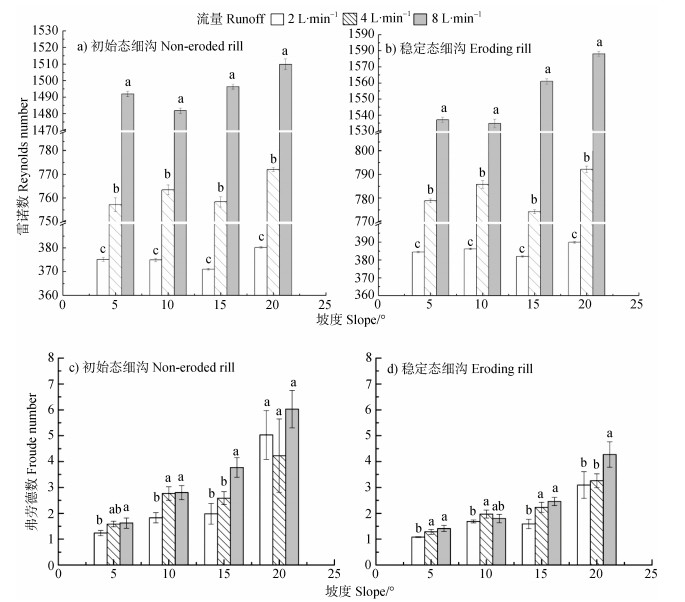
水流流态可分为层流(Re < 500)、紊流(Re > 2 000)或过渡流(Re=500~2 000)。流型可分为缓流(Fr < 1)、急流(Fr > 1)或临界流(Fr=1)。
当流量为2 L·min–1时,Re值小于500,为层流,在流量为4和8 L·min–1时,Re值介于500~2 000之间,为过渡流(图 5)。Re值在流量处理间差异显著,随着流量增加,水流从层流变为过渡流。Re值在坡度处理间无显著差异(图 6a和6b)。Re值在不同细沟侵蚀阶段无明显差异。
|
图 5 不同坡度下的雷诺数(Re)和弗劳德数(Fr) Fig. 5 Reynolds number(Re)and Froude number(Fr)relative to slope gradient |
|
注:a)初始态雷诺数(ReN);b)稳定态雷诺数(ReE);c)初始态弗劳德数(FrN);d)稳定态弗劳德数(FrE)。 Note:a)Reynolds number of non-eroded rill(ReN),and b)Reynolds number of eroding rill(ReE). c)Froude number of non-eroded rill(FrN),and d)Froude number of eroding rill(FrE) 图 6 不同坡度对雷诺数(Re)和弗劳德数(Fr)的影响 Fig. 6 Effect of slope gradient on Reynolds number(Re)and Froude number(Fr) |
在本试验范围内,各工况下Fr值均大于1(图 5),表明细沟径流在整个细沟发育阶段均属于急流。初始态弗劳德数FrN值介于1.237~6.026之间,稳定态弗劳德数FrE值介于1.079~4.274之间。在同一流量和坡度工况下,初始态弗劳德数FrN>稳定态弗劳德数FrE,且FrE的变化范围相对于FrN更小。在初始态细沟阶段,坡度为5°、10°和15°时,FrN随流量增加而增大,20°时,流量间FrN无显著差异(图 6c),坡度为20°时,FrN在流量为4 L·min–1时小于2 L·min–1,与其他坡度下随流量的变化规律不一致,是因为FrN随流量增加变化较为复杂,从能量的角度分析,尽管流量的增加使水流具有更大的动能,但是在对细沟微地貌进行塑造的过程中消耗了更多的动能,在稳定态细沟阶段,坡度为5°、15°和20°时,FrE随流量增加而增大,10°时,FrE先升高后降低(图 6d)。
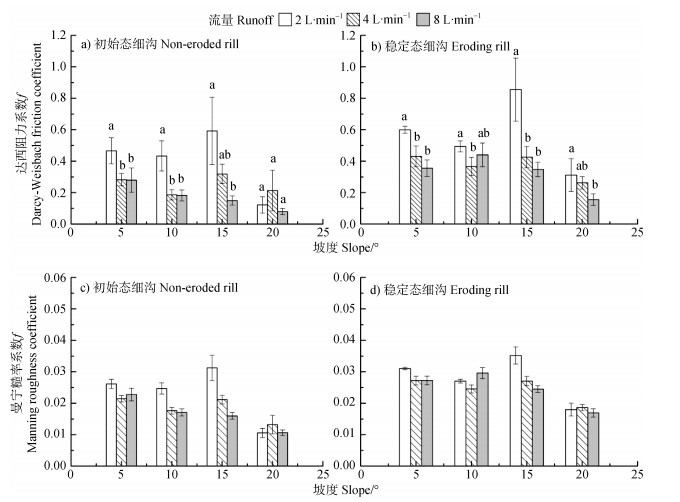
2.3 细沟径流阻力本试验f值介于0.079~0.856之间,n值介于0.011~0.035之间。n随流量和坡度的变化趋势与f一致(图 7),表明f和n对于表达细沟径流阻力结果是基本一致的。
|
注:a)初始态达西阻力系数(fN);b)稳定态达西阻力系数(fE);c)初始态曼宁糙率系数(nN);d)稳定态曼宁糙率系数(nE)。 Note:a)Darcy-Weisbach friction coefficient of non-eroded rill(fN),and b)Darcy-Weisbach friction coefficient of eroding rill(fE). c)Manning roughness coefficient of non-eroded rill(nN),and d)Manning roughness coefficient of eroding rill(nE). 图 7 不同坡度对达西阻力系数(f)和曼宁糙率系数(n)的影响 Fig. 7 Effect of slope gradient on Darcy-Weisbach friction coefficient(f)and Manning roughness coefficient(n) |
初始态细沟达西阻力系数fN介于0.079~0.592之间,稳定态细沟达西阻力系数fE介于0.156~0.856之间,在同一流量和坡度工况下,初始态达西阻力系数fN<稳定态达西阻力系数fE。初始态细沟在坡度为5°、10°和15°时,fN随流量增加而减小,在20°时有小的波动,因为坡度变大,径流重力沿坡面分力增加,加之流量增加促使细沟侵蚀加剧,细沟微地貌更加复杂,使得水流阻力增强,而稳定态细沟在10°时有小的波动。初始态细沟在流量为2和4 L·min–1时,fN随坡度增加呈先减小后增大再减小的波动状,流量为8 L·min–1时,呈逐渐减小的趋势,而稳定态细沟在流量为8 L·min–1时随坡度增加先增大后减小至最小值。上述结果表明初始态和稳定态细沟的f随流量和坡度的变化规律存在差异。
3 讨论关于细沟径流阻力的研究,现有的试验结果差别较大。任熠等[22]在5°~25°坡度范围内,紫色土细沟流f值介于0.195~0.975之间;李占斌等[23]在流量介于6.5~10.5 L·min–1,坡度介于21°~27°的陡坡上进行试验,结果表明黄土坡面上形成细沟的f值介于0.10~0.60之间;丁文峰等[24]在6°~12°的坡度范围内进行流量介于2.4~6.5 L·min–1的放水冲刷试验,f值不超过0.65。可见紫色土细沟阻力相对黄土较大,这是由于紫色土与黄土土壤性质的差异,同理,饱和与非饱和土在土壤性质上同样存在差异。因此,有必要基于特定的试验范围,探究流量、坡度以及不同细沟侵蚀阶段对细沟水力学特征的影响。
3.1 流量和坡度对流速和平均径流深的影响为了解流量和坡度对不同细沟侵蚀阶段流速(V)和平均径流深(h)的影响程度的差异,采用逐步多元回归方法对实测资料进行模拟。由拟合方程可知,尽管V和h在不同细沟侵蚀阶段随流量和坡度的变化规律一致,但其在不同细沟侵蚀阶段的贡献率存在差异。V与流量和坡度间均呈幂函数正相关关系,但式(7)的流量和坡度指数均小于式(6),h与流量间呈幂函数正相关关系,h与坡度间呈幂函数负相关关系,但式(9)的流量指数大于式(8),坡度指数小于式(8)。
| $ V_N = 0.346 \cdot {Q^{0.524}} \cdot {S^{0.601}}, \; R^2=0.910 $ | (6) |
| $ V_E = 0.298 \cdot {Q^{0.474}} \cdot {S^{0.530}}, R^2=0.905 $ | (7) |
| $ h_N = 2.483 \cdot {Q^{0.502}} \cdot {S^{ - 0.505}}, R^2=0.942 $ | (8) |
| $ h_E = 2.766 \cdot {Q^{0.558}} \cdot {S^{ - 0.415}},R^2=0.942 $ | (9) |
式中,VN为初始态细沟流速,m·s–1;VE为稳定态细沟流速,m·s–1;hN为初始态细沟平均径流深,cm;hE为稳定态细沟平均径流深,cm;S为坡度,°;Q为流量,10–3 m3·s–1。
拟合结果表明,坡度对流速的影响大于流量。在不同细沟侵蚀阶段,随着细沟的发展,流量和坡度对V的影响减小。这是因为流量和坡度可通过改变细沟形态间接影响V[25],而细沟在稳定态阶段的形态不会发生大幅度改变;此外,随着细沟的发展,流量对h的影响增大,而坡度对h的影响减小。从h的计算公式可知,流量对h有直接促进作用,而坡度会通过影响V从而间接抑制h,在稳定态细沟阶段坡度对V的影响减小导致对h的影响也减小,流量在初始态细沟阶段会消耗一部分水流能量作用于细沟形态的改变。因此,为减小细沟侵蚀进一步演变的可能性,在防治细沟侵蚀发育的实践过程中,坡度应优于流量作为重要因子,初始态细沟应先于稳定态细沟作为重要阶段进行防控。
3.2 不同细沟侵蚀阶段对水力学参数的影响由试验结果可知,水力学参数在不同细沟侵蚀阶段存在差异。细沟在从初始态到稳定态的发育过程中,V值减小,h值增大,Re值增大,Fr值减小,f值和n值增大,表明细沟径流对稳定态细沟的侵蚀强度相对于初始态细沟较小。主要原因在于:(1)发育过程中细沟沟底微地貌的变化,最显著的特征在于跌坎(图 8a)的产生,而跌坎对水流存在消能作用;(2)水流冲刷后裸露出更多的碎屑(图 8b),导致坡面粗糙度的增加,对径流的阻滞作用加强[26],从消能和阻滞作用两个方面降低细沟流速,壅高径流深,在流速和平均径流深的综合作用下导致流态和阻力发生改变。

|
图 8 细沟侵蚀阶段中出现的现象:a)跌坎;b)碎屑 Fig. 8 Phenomenon appearing during rill erosion: a)Step-down floor; b)Rock fragment |
Grant [27]推断,坡面在还未受到水流影响且相对较为光滑时会产生急流,当坡面形态受到水流影响后Fr值趋近于1,即在坡面侵蚀过程中水流有从急流向临界流转变的趋势。Giménez和Govers[28]进一步发现,在稳定态细沟中,Fr值会在流速和平均径流深的调节下保持相对稳定。本研究符合Grant [27]、Giménez和Govers[28]的试验结果:FrE的变化范围(1.079~4.274)相对于FrN(1.237~6.026)较小,表明在稳定态细沟阶段,Fr值保持相对稳定且趋近于1。
细沟发育过程中,水流能量降低,阻力增大,这符合Wang等[29]在侵蚀后期f值增大的研究结果。由f的计算公式可知,f受V和h的综合作用,其中V对f存在抑制作用,而h对f存在促进作用。一方面,坡度增大会通过增加坡面粗糙度间接抑制V,从而促进f,另一方面,流量增加促进h,从而促进f。在稳定态细沟,其形态不会发生大的改变,坡面粗糙度不会因为坡度的增加而大幅度增加,即通过V影响f的作用会降低,因此,在初始态细沟中V占主要作用,稳定态细沟中h占主要作用,稳定态细沟阻力特征与Li等[30]的研究结果一致。
4 结论同一流量和坡度工况下,初始态细沟流速>稳定态细沟流速。在不同细沟侵蚀阶段,流量和坡度对流速(V)和平均径流深(h)的贡献率存在差异,随着细沟的发展,流量和坡度对V的影响减小,流量和坡度可通过改变细沟形态间接影响V,流量对h的影响增大,坡度对h的影响减小,流量对h有直接促进作用,而坡度会通过影响V从而间接抑制h。Re值在不同细沟侵蚀阶段无明显差异,在流量处理间差异显著。Fr值在整个发育阶段均大于1,属于急流,Fr值在稳定态细沟阶段受到流速和平均径流深的调节保持相对稳定且趋近于1。达西阻力系数(f)在V和h的综合作用下发生改变,在初始态细沟中V占主要作用,稳定态细沟中h占主要作用。饱和紫色土细沟从初始态到稳定态的发育过程中,V值减小,h值增大,Re值增大,Fr值减小,f值和n值增大,细沟径流对稳定态细沟的侵蚀强度相对于初始态细沟较小。这是因为细沟形态的改变,加强了对细沟径流的消能和阻滞作用,从而V减小,h增大,最终导致流态和阻力在不同细沟侵蚀阶段的差异。
| [1] |
Zheng F L, Huang C H, Norton L D. Effects of near-surface hydraulic gradients on nitrate and phosphorus losses in surface runoff[J]. Journal of Environmental Quality, 2004, 33(6): 2174-2182. DOI:10.2134/jeq2004.2174
(  0) 0) |
| [2] |
Liu Y J, Yang J, Hu J M, et al. Characteristics of the surface-subsurface flow generation and sediment yield to the rainfall regime and land-cover by long-term in situ observation in the red soil region, Southern China[J]. Journal of Hydrology, 2016, 539: 457-467. DOI:10.1016/j.jhydrol.2016.05.058
(  0) 0) |
| [3] |
Niu J, Zhang P C, Xing M X. Characteristics of soil and water loss on purple slope farmland and its control in upper reaches of the Yangtze River (In Chinese)[J]. Science of Soil and Water Conservation, 2010, 8(6): 64-68. DOI:10.3969/j.issn.1672-3007.2010.06.012 [牛俊, 张平仓, 邢明星. 长江上游紫色土坡耕地水土流失特征及其防治对策[J]. 中国水土保持科学, 2010, 8(6): 64-68.]
(  0) 0) |
| [4] |
Sun W Y, Mu X M, Gao P, et al. Landscape patches influencing hillslope erosion processes and flow hydrodynamics[J]. Geoderma, 2019, 353: 391-400. DOI:10.1016/j.geoderma.2019.07.003
(  0) 0) |
| [5] |
Zhang L T, Gao Z L, Yang S W, et al. Dynamic processes of soil erosion by runoff on engineered landforms derived from expressway construction: A case study of typical steep spoil heap[J]. Catena, 2015, 128: 108-121. DOI:10.1016/j.catena.2015.01.020
(  0) 0) |
| [6] |
Lei T W, Xia W S, Zhao J, et al. Method for measuring velocity of shallow water flow for soil erosion with an electrolyte tracer[J]. Journal of Hydrology, 2005, 301(1): 139-145.
(  0) 0) |
| [7] |
Lei T W, Chuo R Y, Zhao J, et al. An improved method for shallow water flow velocity measurement with practical electrolyte inputs[J]. Journal of Hydrology, 2010, 390(1/2): 45-56.
(  0) 0) |
| [8] |
Gómez J A, Darboux F, Nearing M A. Development and evolution of rill networks under simulated rainfall[J]. Water Resources Research, 2003, 39(6): 1148-1161.
(  0) 0) |
| [9] |
He J J, Sun L Y, Cai Q G, et al. Characteristics of rill development on slope and theirs effects on flow velocity distribution (In Chinese)[J]. Acta Pedologica Sinica, 2013, 50(5): 862-870. [和继军, 孙莉英, 蔡强国, 等. 坡面细沟发育特征及其对流速分布的影响[J]. 土壤学报, 2013, 50(5): 862-870.]
(  0) 0) |
| [10] |
Cai Q G. Research of rill initiation condition on loess hillslopes (In Chinese)[J]. Journal of Sediment Research, 1998(1): 52-59. [蔡强国. 坡面细沟发生临界条件研究[J]. 泥沙研究, 1998(1): 52-59.]
(  0) 0) |
| [11] |
Hao H X, Guo Z L, Wang X Z, et al. Rill erosion process on red soil slope under interaction of rainfall and scouring flow (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(8): 134-140. [郝好鑫, 郭忠录, 王先舟, 等. 降雨和径流条件下红壤坡面细沟侵蚀过程[J]. 农业工程学报, 2017, 33(8): 134-140.]
(  0) 0) |
| [12] |
Govers G. Relationship between discharge, velocity and flow area for rills eroding loose, non-layered materials[J]. Earth Surface Processes and Landforms, 1992, 17(5): 515-528. DOI:10.1002/esp.3290170510
(  0) 0) |
| [13] |
Nearing M A, Norton L D, Bulgakov D A, et al. Hydraulics and erosion in eroding rills[J]. Water Resources Research, 1997, 33(4): 865-876. DOI:10.1029/97WR00013
(  0) 0) |
| [14] |
Huang Y H, Chen X Y, Li F H, et al. Velocity of water flow along saturated loess slopes under erosion effects[J]. Journal of Hydrology, 2018, 561: 304-311. DOI:10.1016/j.jhydrol.2018.03.070
(  0) 0) |
| [15] |
He J J, Sun L Y, Gong H L, et al. Comparison of rill flow velocity regimes between developing and stationary rills[J]. Catena, 2018, 167: 13-17. DOI:10.1016/j.catena.2018.04.020
(  0) 0) |
| [16] |
Zhang G H, Hu J J. Effects of patchy distributed Artemisia capillaris on overland flow hydrodynamic characteristics[J]. International Soil and Water Conservation Research, 2019, 7(1): 81-88. DOI:10.1016/j.iswcr.2018.12.003
(  0) 0) |
| [17] |
Lei T W, Zhang Q W, Yan L J. Rill erosion physical model (In Chinese). Beijing: Science Press, 2009. [雷廷武, 张晴雯, 闫丽娟. 细沟侵蚀物理模型[M]. 北京: 科学出版社, 2009.]
(  0) 0) |
| [18] |
Chen X Y, Huang Y H, Zhao Y, et al. Analytical method for determining rill detachment rate of purple soil as compared with that of loess soil[J]. Journal of Hydrology, 2017, 549: 236-243. DOI:10.1016/j.jhydrol.2017.03.065
(  0) 0) |
| [19] |
Xing H, Chen X Y, Han Z, et al. Comparation of hydrodynamic characteristics and flow resistance under rill erosion between saturated and unsaturated loess soil (In Chinese)[J]. Journal of Soil and Water Conservation, 2018, 32(3): 92-97. [邢行, 陈晓燕, 韩珍, 等. 饱和与非饱和黄绵土细沟径流水动力学特征及侵蚀阻力对比[J]. 水土保持学报, 2018, 32(3): 92-97.]
(  0) 0) |
| [20] |
Dong Y Q, Zhuang X H, Lei T W, et al. Optimum measurement distance of water flow velocity over frozen slopes with pulse boundary model method (In Chinese)[J]. Transactions of The Chinese Society of Agricultural Machinery, 2015, 46(2): 146-152. [董月群, 庄晓晖, 雷廷武, 等. 脉冲边界模型测量冻土坡面径流流速与距离优选[J]. 农业机械学报, 2015, 46(2): 146-152.]
(  0) 0) |
| [21] |
Lei T W, Yan Y, Shi X N, et al. Measuring velocity of water flow within a gravel layer using an electrolyte tracer method with a Pulse Boundary Model[J]. Journal of Hydrology, 2013, 500: 37-44. DOI:10.1016/j.jhydrol.2013.07.025
(  0) 0) |
| [22] |
Ren Y, Wang X T, Wang Y K, et al. Study on hydrodynamic characters of rill flow on purple soil slope (In Chinese)[J]. Journal of Soil and Water Conservation, 2007, 21(6): 39-42, 46. DOI:10.3321/j.issn:1009-2242.2007.06.009 [任熠, 王先拓, 王玉宽, 等. 紫色土坡面细沟流的水动力学特征试验研究[J]. 水土保持学报, 2007, 21(6): 39-42, 46.]
(  0) 0) |
| [23] |
Li Z B, Qin B S, Kang W, et al. Indoor experimental studies on hydrodynamic characteristics of runoff in rill erosion procession steep slope (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(6): 64-68. DOI:10.3321/j.issn:1002-6819.2008.06.013 [李占斌, 秦百顺, 亢伟, 等. 陡坡面发育的细沟水动力学特性室内试验研究[J]. 农业工程学报, 2008, 24(6): 64-68.]
(  0) 0) |
| [24] |
Ding W F, Li Z B, Ding D S. Study on hydrodynamic characters of runoff in rill erosion process on slope (In Chinese)[J]. Journal of Soil and Water Conservation, 2002, 16(3): 72-75. DOI:10.3321/j.issn:1009-2242.2002.03.019 [丁文峰, 李占斌, 丁登山. 坡面细沟侵蚀过程的水动力学特征试验研究[J]. 水土保持学报, 2002, 16(3): 72-75.]
(  0) 0) |
| [25] |
Nearing M A, Polyakov V O, Nichols M H, et al. Slope-velocity equilibrium and evolution of surface roughness on a stony hillslope[J]. Hydrology and Earth System Sciences, 2017, 21(6): 3221-3229. DOI:10.5194/hess-21-3221-2017
(  0) 0) |
| [26] |
Giménez R, Planchon O, Silvera N, et al. Longitudinal velocity patterns and bed morphology interaction in a rill[J]. Earth Surface Processes and Landforms, 2004, 29(1): 105-114. DOI:10.1002/esp.1021
(  0) 0) |
| [27] |
Grant G E. Critical flow constrains flow hydraulics in mobile-bed streams: A new hypothesis[J]. Water Resources Research, 1997, 33(2): 349-358. DOI:10.1029/96WR03134
(  0) 0) |
| [28] |
Giménez R, Govers G. Interaction between bed roughness and flow hydraulics in eroding rills[J]. Water Resources Research, 2001, 37(3): 791-799. DOI:10.1029/2000WR900252
(  0) 0) |
| [29] |
Wang L J, Zhang G H, Wang X, et al. Hydraulics of overland flow influenced by litter incorporation under extreme rainfall[J]. Hydrological Processes, 2019, 33(5): 737-747. DOI:10.1002/hyp.13358
(  0) 0) |
| [30] |
Li T Y, He B H, Chen Z P, et al. Effects of gravel on concentrated flow hydraulics and erosion in simulated landslide deposits[J]. Catena, 2017, 156: 197-204. DOI:10.1016/j.catena.2017.04.015
(  0) 0) |
 2022, Vol. 59
2022, Vol. 59


