2. 浙江省农业资源与环境重点实验室, 杭州 310058
2. Zhejiang Provincial Key Laboratory of Agricultural Resources and Environment, Zhejiang University, Hangzhou 310058, China
工业革命后,城市化、工业化的浪潮持续高涨,造成了人类对自然环境的强烈改变,严重威胁着自然经济社会的可持续发展[1]。健康风险评价应时而生,其可识别量化污染环境介质对人体可能产生的危害或损失[2]。土壤作为重要的环境介质之一,因开放包容的体系,重金属累积问题日益突出,并呈现出从局域到区域的蔓延态势,从缓慢积累到迅猛爆发的上升阶段[3]。面对人居健康及食品安全的巨大压力,如何准确、深入识别土壤重金属污染对人体造成的健康危害,进而强化精准、有效的土壤重金属污染风险管控显得尤为关键。国内外已经有众多学者及相关研究机构对此进行了不懈的探索,相继提出了毒物鉴定法、体内外模拟试验(in vitro and in vivo)、剂量-反应关系(dose-response relation)等相关风险评估概念[4]。在此基础上,还开发出“四步走”确定性健康风险评估[5]及多介质综合暴露风险评估[6]等多种风险分析模型,为土壤重金属暴露风险量化做出了重要贡献,极大地促进了土壤环境风险基准及管理体系的完善和发展。
然而,土壤重金属污染本身具有污染源多、持久性强、危害面广的特点[7],且不同生命阶段或人群所经历的风险差异巨大,多变性、动态性、随机性贯穿土壤重金属污染健康风险传递的全过程[8]。此外,风险管理时间、精力等成本有限,往往造成健康风险评估存在高度不确定性和潜在复杂性[9]。因此,如何处理土壤重金属污染健康风险评估中的不确定和变异性早已成为土壤环境风险评估领域的研究焦点[10]。
在此背景下,概率风险评估(Probabilistic Risk Assessment,PRA)应运而生。有别于以单点值为输出的传统确定性风险评估(Deterministic Risk Assessment,DRA)方法,其以处理不确定性及变异性对风险评估造成的影响为出发点,提供了暴露风险的范围和可能性的估计,避免了高估或低估健康风险,可弥合风险决策制定者与分析者的沟通差距,促进风险管理和决策的改进[11]。近年来,应用PRA处理风险评估不确定性已成为土壤污染风险评估领域的新趋势。Cao等[12]通过对比DRA与PRA计算所得土壤铅暴露单点非致癌均值,验证了DRA计算的风险值会低估该地区儿童土壤铅暴露风险。但是迄今少有相关研究对概率健康风险评估的适用范围、具体步骤、技术方法以及发展演变做出系统的梳理和归纳。部分土壤重金属污染概率风险评估文献还存在着对概率风险理论认识不清、适用范围不明的问题,这可能导致概率风险输出结果严重偏离实际,不利于其后期应用。
基于此,本文拟对概率健康风险评估的理论基础及演变历程进行系统回顾总结,进而将其与确定性风险评估进行对比,深入剖析其面临的挑战及未来展望,以期促进概率风险评估在土壤环境风险评估领域及管理体系中的应用和可持续发展。
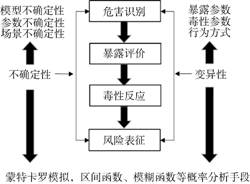
1 概率风险评估的理论基础及框架外延 1.1 理论基础概率风险评估框架是将变异性和不确定性纳入健康或生态风险评估过程的一组理念和技术集成[11]。区别于传统的确定性单点风险评估,其提供了人体或整个生态系统遭受危害的范围和可能性的估计(图 1)。该框架以尽可能定量化表征不确定性及变异性对风险评估造成的影响为关键,以改善健康风险管理决策和保护人类健康为宗旨,适用于以下情况:(1)有必要披露单点风险估计的偏倚程度时;(2)需要对敏感物种、暴露途径、污染源头进行优先排序时;(3)确定性风险评估方法筛查得出风险较高且风险管理成本较高时[13]。满足上述情况,应用概率风险分析方法可优化风险评估结果。反之,通过初期筛查发现风险值远低于风险阈值且污染修复措施成本非常低时,概率风险评估通常并不需执行。
|
图 1 概率风险评估理念图 Fig. 1 Conceptual diagram of probabilistic risk assessment |
风险评估不确定类型包括参数不确定性(测量误差、采样误差及系统误差),模型不确定性(模型结构不符合实际流程、模型错误使用及使用不合适的替代数据)和场景不确定性(描述性错误、专业判断错误及不完整的分析)等[14-15]。对风险参数、模型及情景的错误判断可能导致高估或低估健康风险,将直接影响风险管理措施的科学性和实效性。而变异性则指人群暴露、毒性参数的异质性和多样性,其源于种间生理及行为差异。例如,人类的生理变化(如体重、身高、土壤摄入率),土壤和其他介质中污染物浓度差异[11]。变异性通常不可减少但可通过扩大实测研究实现优化表征。环境系统复杂多变,因人类研究范围及认知能力极为有限,缺乏对真实世界有关特定因素、参数或模型的了解,且又受到时空尺度效应的制约,健康风险评估中的不确定性和变异性难以避免。因此,加强对风险评估中的不确定性和变异性的研究,深化对不确定性和变异性类型及处理的认知,有助于增强对概率风险评估科学内涵的理解。
1.2 技术手段常见的不确定风险分析模型有泰勒简化法、概率树法、和蒙特卡罗模拟等[16]。蒙特卡罗模拟(Monte Carlo Simulation,MCS)是最常用的概率风险分析方法,其可将风险事件发生的概率转变为频率,在确定暴露参数先验分布下可生成随机数进行迭代运算,输出以概率分布的形式表达,结合敏感性分析,其还可同时确定与模型输出变异高度相关的参数,为风险值优化提供依据[17]。近年来,蒙特卡罗模拟方法已成功运用于工矿区[18]、城市[19]、农田[20]等多区域土壤重金属暴露风险分析,并基于概率风险输出识别优先控制元素及关键暴露参数。此外,概率风险方法也被用于土壤邻苯二甲酸酯、多环芳烃等有机污染的健康风险评估中[21]。与使用确定性风险评价模型相比,概率风险模拟可提供污染风险超过阈值的概率,避免健康风险值出现较大评估偏差,为实现精准的风险管控及修复措施提供科学依据。
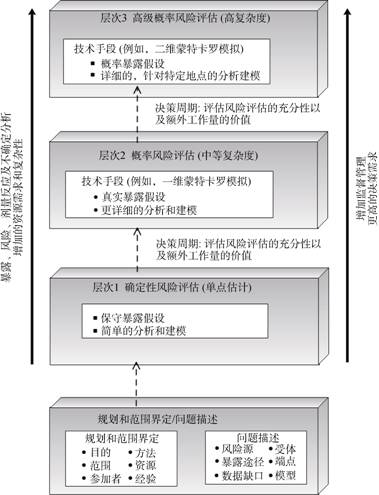
1.3 框架外延概率风险评估理念引起了环境风险评估领域的广泛热议,但参数分布如何定义,是否需要更多的数据、时间和精力,其对环境风险管理是否真正有效一直是争议的焦点。美国环保署(USEPA)及国家研究委员会(NRC)对学界的讨论给予了积极的回应,开发并建议使用分层概率风险评估方法[13](图 2)。所做的调整包括:(1)将确定性单点评估作为概率风险分析的较低层级,设置过渡到较高层次的概率风险评估系统过程;(2)较高的层级反映了风险估计中变异性和不确定性的不断增加,层次过渡需要评估风险分析的充分性以及额外风险评估工作的价值。
|
(本图在参考文献[13]的基础上改动而来) 图 2 分层概率风险评估框架示意图 Fig. 2 Schematic of the framework of tier probabilistic risk assessment(adapted from reference [13]) |
从参数输入、评估工具及风险输出三个方面,对概率风险评估和传统确定性风险评估进行比较(表 1)。
|
|
表 1 概率风险评估与传统确定性风险评估的对比 Table 1 Comparison of probabilistic risk assessment and traditional deterministic risk assessment |
DRA将单个点估计值作为暴露评价模型的输入,其通常使用集中趋势值(Central tendency)来估计最可能的风险值[5]。而PRA输入暴露参数可能的值以及范围,并估计这些值出现的概率[22]。
2.2 评价工具DRA使用USEPA推荐的保守的“四步法”健康评价模型,主要包括危害识别、暴露评估、暴露-剂量反应及风险表征等四个步骤,且使用基于点估计的敏感性分析方法计算各变量对风险输出的贡献度[5]。以经口摄入途径下土壤重金属暴露为例,可通过下式进行摄入暴露剂量(ADD)评估[5]:
| $ {\text{ADD}} = \frac{{C \times {\text{IRsoil}} \times {\text{EF}} \times {\text{ED}}}}{{{\text{BW}} \times {\text{AT}}}} $ |
式中,C为土壤重金属浓度(mg·kg–1);IRsoil为土壤日均摄入量(mg·d–1);EF、ED、AT分别为暴露频率(d·a–1)、暴露持续时间(a)及接触受污染土壤的平均时间(d);BW为暴露个体的体重(kg)。暴露剂量确定后,非致癌风险及致癌风险分别通过危害熵值(HQ)及累计致癌概率(CR)来表征[5]:
| $ {\text{HQ}} = \frac{{{\text{ADD}}}}{{{\text{RfD}}}} $ |
| $ {\text{CR}} = {\text{ADD}} \times {\text{SF}} $ |
式中,RfD代表各种途径下重金属暴露的参考剂量(mg·kg–1·d–1);SF为暴露于土壤重金属的致癌斜率因子(mg·kg–1·d–1)–1。HQ与CR阈值分别为1和10–6[5]。
PRA仍基于确定性风险评价公式,通过方程f = g(X1,X2,X3…Xk)计算,式中X1、X2、X3至Xk代表k个按照一定概率分布的输入随机参数,代入到确定性风险评价模型中进行不确定仿真。以土壤重金属概率风险评估为例,分别赋予土壤中重金属浓度、人体体重、土壤摄入量等各参数概率分布,使用蒙特卡罗模拟等多种模型进行成千上万次迭代运算,依靠得到的一系列风险值输出概率分布,并基于概率风险输出进行变量敏感度分析[23]。
2.3 结果输出DRA输出为暴露量及风险值的单点估计值,且可基于简单的点估计值直接确定不同暴露途径、人群及元素的优先次序,其不需要过多的数据且风险结果简单易懂[13]。相比之下,PRA输出暴露量及风险值的范围及可能性,其能更好地表征风险评估中的不确定性和变异性,适用于更精细的暴露人群、暴露途径及元素的优先级识别。但概率风险评估需专业的培训和指导来传达和应用概率风险结果[24]。因此,对于风险管理体系,DRA与PRA呈现较强的互补性。
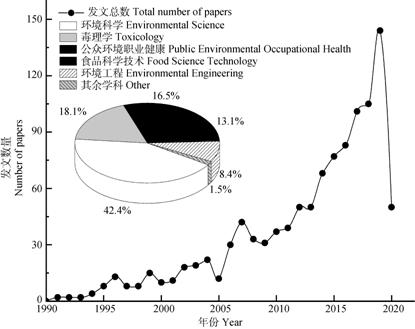
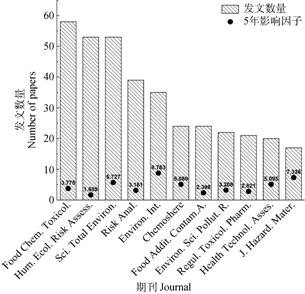
3 概率健康风险评估的应用及发展为更好地展现概率风险分析在环境健康风险评估领域的研究动态,本文利用Web of Science(WoS)核心数据库进行文献检索,检索词设置为probabilistic health risk assessment,文献类型精炼为review和article,全部文献检索日期为2020年5月18日。综合采用WoS自带分析工具、CiteSpace软件与HistCite软件对1990—2020年间发表的1094篇文献进行学科及期刊分布、研究热点及发展趋势多元分析。WoS自带分析工具及HistCite分析结果表明:(1)概率健康风险分析发文量总体呈逐年增加趋势(图 3),其中2019年发文量最多(131篇),且归属于环境科学和毒理学的论文最多(发文662篇,占比达60%),说明概率健康风险评估日益受到重视;(2)文章被发表在70余种刊物上,其中发文数量Top 3期刊是 Food Chemical Toxicology(发文58篇)、Science of the Total Environment(53篇)及Human and Ecological Risk Assessment(发文53篇)(图 4)。
|
图 3 1990—2020年发文总数及各学科占比 Fig. 3 Total number of the papers published during 1990-2020 and proportion relative to discipline |
|
图 4 1990—2020年概率健康风险评估领域发文10篇以上期刊统计 Fig. 4 Journals publishing(more than 10)papers on probabilistic health risk assessment during 1990-2020 |
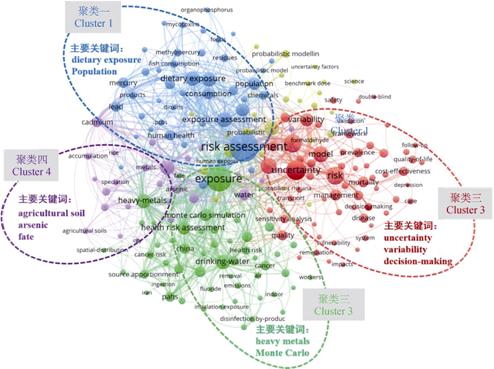
利用Vosviewer对研究关键词合作网络进行可视化共现分析。根据关键词共现网络(图 5),risk assessment是出现最多的关键词,其次为exposure及uncertainty。概率健康风险评估领域关键词可划分为4个关键集聚。关键词集聚一主要针对人群膳食摄入暴露进行健康风险评估,主要关键词为膳食暴露(dietary exposure)、人群(population)、人体健康(human health)。集聚二则聚焦于不确定性和变异性处理及风险管理,包括的主要关键词为不确定性(uncertainty)、变异性(variability)、模型(model)、管理(management)以及决策制定(decision-making)。关键词集聚三则主要聚焦基于蒙特卡罗模拟的重金属暴露风险评估,主要关键词有重金属(heavy metals)、蒙特卡罗模拟(Monte Carlo Simulation)等。集聚四则重点关注农田土壤重金属的环境归趋(主要为镉及砷)及暴露风险评估,主要关键词为农田土壤(agricultural soil)、归趋(fate)等。此外,利用CiteSpace软件对概率风险评估领域近5年关键词突现指标进行分析(表 2),发现不确定性(uncertainty)、生活质量(quality of life)、重金属(heavy metals)及人群(population)突现强度较高。进一步归纳总结,目前概率健康风险评估领域主要研究趋势见表 2。
|
图 5 1990—2020年概率健康风险评估相关研究热点共现网络 Fig. 5 Keywords co-occurrence network for researches relevant to probabilistic health risk assessment during 1990-2020 |
|
|
表 2 近5年概率健康风险评估相关研究关键词突现强度统计 Table 2 Top 8 keywords the strongest in citation burst in the recent 5 years |
概率风险分析的核心挑战在于验证概率分布输入及风险输出结果是否可靠。Clyde和Sullivan[25]早期开发了一种基于贝叶斯方法的框架来评估概率风险模型预测准确性的方法,该方法围绕参数估计的不确定性边界,选择最能解释给定数据的模型,从而实现对参数估计的优化。Lin等[26]则应用贝叶斯框架,将模型参数的先验知识与暴露剂量结合起来以量化不确定性和可变性。在贝叶斯框架下,最常用的是马尔科夫链蒙特卡罗模拟(Markov Chain Monte Carlo,MCMC)。针对数据不符合明确概率分布的情况下,使用该方法可以通过描述观测数据的数学形式(即似然函数)来估计概率分布[13]。此外,模糊方法也被引入风险评估不确定性及变异性的优化处理中,其将不确定性及变异性表示为区间函数[22],已用于污染场地人体健康风险及污染物食物网累积等多种暴露情景[27-28]。然而,场景是分析不确定性的潜在关键来源,其中包括污染物来源、运输途径、接触途径、地理范围等多个复杂变量。目前缺乏对暴露场景中的不确定性定量处理的正式方法,未来仍需要开发出更多的模型优化表征场景不确定性。
3.2 基于改进蒙特卡罗方法的概率健康风险评估尽管蒙特卡罗方法灵活简单,应用最广,但蒙特卡罗方法在随机数的产生和联合分布的确定方面过多地依赖于假定好的分布和模型,且蒙特卡罗法在分析可靠度时,必须先形成一系列可靠的随机数。因此,开发更简单、高效的蒙特卡罗方法以提升随机数的准确性也是当前概率风险领域研究热点之一。张建龙等[29]利用Logistic混沌系统方法改进传统蒙特卡罗方法中利用线性同余产生随机数的方法,提高了随机数输入的可靠性程度。此外,更高级的二维蒙特卡罗(2D Monte Carlo)模拟也被运用于健康风险评估中。Simon等[30]认为二维蒙特卡罗模拟可以进一步处理暴露剂量的个体间内在变异,并捕获剂量参数不确定性的影响,尤其是在缺少暴露参数实测数据时,可纠正简单蒙特卡罗模拟导致的误差。Wang等[31]通过二维蒙特卡罗方法评估了华北地区灌溉工人和公众暴露于循环水中三卤甲烷的健康风险,对变量执行内外部仿真进一步区别不确定和变异性,成功识别风险最高、最低等关键风险点,提高了健康风险评估的准确性,为不同人群风险控制措施提供了科学依据。空间化概率风险评估是当前蒙特卡罗方法发展的另一趋势。Linkov等[32]曾提出受污染场地概率生态风险评估和受体迁移的整合模型,可结合场地污染受体空间轨迹及蒙特卡罗风险进行分析。尽管现有的空间化概率风险框架大多针对生态风险[33],但未来蒙特卡罗方法也可与地统计方法相结合,识别不同区域人群暴露于土壤重金属污染的健康风险超标率,为土壤重金属暴露风险分区管控提供技术支撑[34]。
3.3 与重金属源解析、毒代动力学等模型及生物靶标分析的整合近年来,研究者对土壤重金属污染溯源及风险传递给予极大关注,系统剖析土壤重金属跨介质暴露风险已成为研究前沿。土壤重金属相关风险涉及环境过程(例如,大气沉积和径流输入)、食物网转移(例如,生物蓄积)和环境健康效应(例如,重金属摄入量和暴露剂量-反应),这是一个多介质、多途径的复杂交互过程[35]。Caudeville等[6]首次建立了综合污染源、环境介质、风险评估、生物监测、社会经济和健康数据的空间随机多介质暴露模型,评价了法国北部加莱海峡当地多种环境介质(空气、土壤、水)转移到个体的风险,提供了分析地理位置、环境与人群健康内在关系的对策。Liu等[36]则开发了一种多媒介建模方法,成功估算中国典型电子废物区周边农田系统整个土壤-水稻-人类链条中镉污染对人体健康的影响。然而,用于源排放、土壤质量、重金属暴露-剂量反应评估的模型具有不同的公式和时空尺度。前人研究采用的确定性风险评估方法显然已不能处理尺度效应带来的不确定性。因此,概率风险评估与环境过程多个模型之间的耦合对深入揭示土壤重金属从源到人体的健康效应具有重要意义。但进行综合评估时,将此类模型整合到统一框架存在技术挑战。此外,将概率健康风险评估与基于生物标志物(例如血铅、尿镉、氧化应激水平等)的长期监测计划相结合,可减少参考剂量水平信息缺失导致的不确定性,并启示后续的风险干预措施[37]。因此,未来还需探索研发土壤污染多介质、多受体概率风险集成分析工具,进一步拓展概率健康风险分析的应用范围。
3.4 概率健康风险分析结果在土壤环境风险决策及管理中的实质应用概率健康风险评估结果可用于识别有效的管理选项,从而做出改善环境质量并节省更多资源成本的决策[38]。相比确定性健康风险评估,执行概率风险评估通常需要更详细、更复杂的分析和更多的资源成本,这可能导致风险管控的延迟。此外,公众对环境健康风险的认知也影响着公众对于风险管理政策的接受度[39]。因此,未来还需关注人群对健康风险的感知和了解,增强评估人员和管理层级对概率风险分析工具的使用能力,通过分享经验和强化培训以推进概率风险评估在环境风险决策及管理中的高效运用[40]。
4 概率风险评估在土壤重金属污染风险评价中的应用与展望本文从理论基础、框架外延、发展应用等方面对概率风险评估相关研究进行了系统的梳理,并将其与传统确定性风险评估进行了深入对比。概率风险评估是从整个生态系统和人群的健康出发,将变异性和不确定性纳入环境风险评估过程的一组理念及技术集成,其突破了环境风险的保守单点估计,给出风险值的范围及可能性,适用于暴露风险的精细评估,为土壤污染健康风险评估提供了一种全新视角,更是对传统确定性健康风险评估研究的重要补充。概率风险评估拓展至分层概率风险评估框架遵循着从较低层级的单点评估过渡到较高层次的概率风险评估的路径,较高的层级反映了风险估计中变异性和/或不确定性不断增加。未来如何从环境过程的尺度效应、暴露场景处理及参数边界定义等方面加深对不确定性和变异性的理论研究,提升不确定性和变异性分布设定及结果输出的科学性和实效性,是概率风险分析面临的重要挑战。
综合本文分析,建议未来从如下方面深化概率风险评估框架在土壤重金属污染健康风险评估中的科学内涵和应用价值:(1)理论基础:从土壤污染过程尺度效应、暴露场景处理及参数定义边界等方面对不确定性和变异性进行深入研究,优化概率风险评估参数概率分布设定,增强概率健康风险评估框架的科学性;(2)技术革新:加强蒙特卡罗模拟方法的改进,研发适用于土壤重金属污染环境的空间化概率健康风险分析手段,推进与土壤重金属源解析、毒代动力学及生物靶标分析模型的整合研究,以提升该框架的方法学支撑;(3)实际应用:概率健康风险评估是对传统的确定性风险分析的有益补充,应充分发挥两者在土壤重金属污染健康风险评估中的互补性,将分层概率健风险评估框架逐步运用于土壤环境风险管理等重要公共事务中,为促进土壤环境风险基准及管理体系的发展完善提供方法支撑。
| [1] |
张慧敏. 人类强烈影响地区土壤与灰尘中重金属的污染特征及风险评价[D]. 杭州: 浙江大学, 2017. Zhang H M. Pollution characteristics and risk assessment of heavy metals in soils and dusts from the intensive human impact area[D]. Hangzhou: Zhejiang University. 2017. (  0) 0) |
| [2] |
National Research Council(NRC). Risk assessment in the federal government . Washington D C: National Academies Press, 1983.
(  0) 0) |
| [3] |
Weng B Q, Liu P H, Zhang W L, et al. Ideas and countermeasures research on heavy metal pollution prevention and control for farmland (In Chinese)[J]. Ecology and Environmental Sciences, 2015, 24(7): 1253-1258. [翁伯琦, 刘朋虎, 张伟利, 等. 农田重金属污染防控思路与技术对策研究[J]. 生态环境学报, 2015, 24(7): 1253-1258.]
(  0) 0) |
| [4] |
Zhang A H, Wang D P. Enhancing risk assessment of environmental arsenic pollution on human health (In Chinese)[J]. Chinese Journal of Preventive Medicine, 2018, 52(10): 969-972. DOI:10.3760/cma.j.issn.0253-9624.2018.10.001 [张爱华, 王大朋. 重视环境砷污染健康风险评估研究[J]. 中华预防医学杂志, 2018, 52(10): 969-972.]
(  0) 0) |
| [5] |
United States Environmental Protection Agency(USEPA). EPA/600/R-09/052F Exposure Factors Handbook(Final Edition)[S]. Washington, DC: 2011.
(  0) 0) |
| [6] |
Caudeville J, Bonnard R, Boudet C, et al. Development of a spatial stochastic multimedia exposure model to assess population exposure at a regional scale[J]. Science of the Total Environment, 2012, 432: 297-308. DOI:10.1016/j.scitotenv.2012.06.001
(  0) 0) |
| [7] |
周琼. 场地环境风险评估方法探究——以上海市某场地为例[D]. 上海: 上海交通大学, 2018. Zhou Q. Research on assessment method of site environment -A site in Shanghai as an example[D]. Shanghai, Shanghai Jiao Tong University, 2018. (  0) 0) |
| [8] |
Yao H, Li G B, Zhang J C, et al. Application of Monte-Carlo method in water pollution control theory (In Chinese)[J]. Journal of Harbin Institute of Technology, 2004, 36(1): 129-131. DOI:10.3321/j.issn:0367-6234.2004.01.035 [姚宏, 李圭白, 张景成, 等. 蒙特卡罗方法在水污染控制理论中的应用前景[J]. 哈尔滨工业大学学报, 2004, 36(1): 129-131.]
(  0) 0) |
| [9] |
Yang L, Ma Z W, Bi J. Application of comparative risk assessment in environmental risk management (In Chinese)[J]. Chinese Journal of Environmental Management, 2019, 11(3): 94-99. [杨蕾, 马宗伟, 毕军. 比较风险评价在环境风险管理中的应用[J]. 中国环境管理, 2019, 11(3): 94-99.]
(  0) 0) |
| [10] |
Kentel E, Aral M M. Risk tolerance measure for decision-making in fuzzy analysis: A health risk assessment perspective[J]. Stochastic Environmental Research and Risk Assessment, 2007, 21(4): 405-417. DOI:10.1007/s00477-006-0073-2
(  0) 0) |
| [11] |
Hansen F. Policy for use of probabilistic analysis in risk assessment[R/OL]. USEPA. (1997-05-15)[2012-09-10].http://www.epa.gov/osa/spe/pdfs/prohpol,pdf.
(  0) 0) |
| [12] |
Cao S Z, Duan X L, Zhao X G, et al. Health risk assessment of various metal(loid) s via multiple exposure pathways on children living near a typical lead-acid battery plant, China[J]. Environmental Pollution, 2015, 200: 16-23. DOI:10.1016/j.envpol.2015.02.010
(  0) 0) |
| [13] |
United States Environmental Protection Agency(USEPA). EPA/100/R‐09/001A Risk assessment forum white paper: Probabilistic risk assessment methods and case studies[S]. Washington D C: Risk Assessment Forum, 2014.
(  0) 0) |
| [14] |
Wang J P, Cheng S T, Jia H F. Markov Chain Monte Carlo scheme for parameter uncertainty analysis in water quality model (In Chinese)[J]. Environmental Science, 2006, 27(1): 24-30. [王建平, 程声通, 贾海峰. 基于MCMC法的水质模型参数不确定性研究[J]. 环境科学, 2006, 27(1): 24-30.]
(  0) 0) |
| [15] |
United States Environmental Protection Agency(USEPA). EPA/630/R-97/001 Guiding principles for monte carlo analysis[S]. Washington D C: 1997.
(  0) 0) |
| [16] |
Zhang Y H, Liu Z Q, Li G H, et al. Uncertainty analysis of health risk assessment caused by benzene contamination in a contaminated site (In Chinese)[J]. Environmental Science, 2007, 28(7): 1409-1415. DOI:10.3321/j.issn:0250-3301.2007.07.001 [张应华, 刘志全, 李广贺, 等. 基于不确定性分析的健康环境风险评价[J]. 环境科学, 2007, 28(7): 1409-1415.]
(  0) 0) |
| [17] |
Kentel E, Aral M M. 2D Monte Carlo versus 2D fuzzy Monte Carlo health risk assessment[J]. Stochastic Environmental Research and Risk Assessment, 2005, 19(1): 86-96. DOI:10.1007/s00477-004-0209-1
(  0) 0) |
| [18] |
Qu C S, Kai S, Wang S R, et al. Monte Carlo simulation-based health risk assessment of heavy metal soil pollution: a case study in the Qixia mining area, China[J]. Human & Ecological Risk Assessment: An International Journal, 2012, 18(4): 733-750.
(  0) 0) |
| [19] |
Cao S, Duan X, Zhao X, et al. Health risks of children's cumulative and aggregative exposure to metals and metalloids in a typical urban environment in China[J]. Chemosphere, 2016, 147: 404-411. DOI:10.1016/j.chemosphere.2015.12.134
(  0) 0) |
| [20] |
Yang S, Zhao J, Chang S X, et al. Status assessment and probabilistic health risk modeling of metals accumulation in agriculture soils across China: A synthesis[J]. Environment International, 2019, 128: 165-174. DOI:10.1016/j.envint.2019.04.044
(  0) 0) |
| [21] |
Ginsberg G L, Belleggia G. Use of Monte Carlo analysis in a risk-based prioritization of toxic constituents in house dust[J]. Environment International, 2017, 109: 101-113. DOI:10.1016/j.envint.2017.06.009
(  0) 0) |
| [22] |
Kentel E, Aral M M. Probabilistic-fuzzy health risk modeling[J]. Stochastic Environmental Research and Risk Assessment, 2004, 18(5): 324-338. DOI:10.1007/s00477-004-0187-3
(  0) 0) |
| [23] |
Zhang K, Achari G, Li H, et al. An integrated health risk assessment of contaminated sites under aleatory and epistemic uncertainties[J]. International Journal of Risk Assessment and Management, 2011, 15(1): 4-42. DOI:10.1504/IJRAM.2011.041002
(  0) 0) |
| [24] |
United States Environmental Protection Agency(USEPA). EPA540-R-02-002 Risk assessment guidance for superfund(RAGS): Volume Ⅲ-Part A: Process for conducting probabilistic risk assessment[S]. Washington D C: 2001.
(  0) 0) |
| [25] |
Clyde M P G, Sullivan E. Effects of ambient fine and coarse particles on mortality in Phoenix, Arizona[R]. Washington D C: National Research Center for Statistics and the Environment Technical Report, 2000: 40.
(  0) 0) |
| [26] |
Lin H I, Berzins D W, Myers L, et al. A Bayesian approach to parameter estimation for a crayfish(Procambarus spp.) bioaccumulation mode[J]. Environmental Toxicology and Chemistry, 2004, 23(9): 2259-2266. DOI:10.1897/03-303
(  0) 0) |
| [27] |
Zhang K J, Achari G, Li H, et al. An integrated health risk assessment of contaminated sites under aleatory and epistemic uncertainties[J]. International Journal of Risk Assessment and Management, 2011, 15(1): 4. DOI:10.1504/IJRAM.2011.041002
(  0) 0) |
| [28] |
Regan H M, Hope B K, Ferson S. Analysis and portrayal of uncertainty in a food-web exposure model[J]. Human and Ecological Risk Assessment: An International Journal, 2002, 8(7): 1757-1777. DOI:10.1080/20028091057592
(  0) 0) |
| [29] |
Zhang J L, Xie J C, Wang N, et al. Health risk assessment in the reuse of reclaimed water based on improved Monte Carlo method (In Chinese)[J]. Acta Scientiae Circumstantiae, 2010, 30(11): 2353-2360. [张建龙, 解建仓, 汪妮, 等. 基于改进蒙特卡罗方法的再生水回用健康风险评价[J]. 环境科学学报, 2010, 30(11): 2353-2360.]
(  0) 0) |
| [30] |
Simon S L, Hoffman F O, Hofer E. The two-dimensional Monte Carlo: A new methodologic paradigm for dose reconstruction for epidemiological studies[J]. Radiation Research, 2015, 183(1): 27-41. DOI:10.1667/RR13729.1
(  0) 0) |
| [31] |
Wang C C, Niu Z G, Zhang Y. Health risk assessment of inhalation exposure of irrigation workers and the public to trihalomethanes from reclaimed water in landscape irrigation in Tianjin, North China[J]. Journal of Hazardous Materials, 2013, 262: 179-188. DOI:10.1016/j.jhazmat.2013.08.044
(  0) 0) |
| [32] |
Linkov I, Grebenkov A, Baitchorov V M. Spatially explicit exposure models: Application to military sites[J]. Toxicology and Industrial Health, 2001, 17(5/10): 230-235.
(  0) 0) |
| [33] |
Kapustka L A. Assessing ecological risks at the landscape scale: Opportunities and technical limitations[J]. Ecology and Society, 2005, 10(2): 11. DOI:10.5751/ES-01389-100211
(  0) 0) |
| [34] |
Yang S Y, Zhao J, Chang S X, et al. Status assessment and probabilistic health risk modeling of metals accumulation in agriculture soils across China: A synthesis[J]. Environment International, 2019, 128: 165-174. DOI:10.1016/j.envint.2019.04.044
(  0) 0) |
| [35] |
Chen L, Liang S, Liu M D, et al. Trans-provincial health impacts of atmospheric mercury emissions in China[J]. Nature Communications, 2019, 10: 1484. DOI:10.1038/s41467-019-09080-6
(  0) 0) |
| [36] |
Liu X M, Zhong L B, Meng J, et al. A multi-medium chain modeling approach to estimate the cumulative effects of cadmium pollution on human health[J]. Environmental Pollution, 2018, 239: 308-317. DOI:10.1016/j.envpol.2018.04.033
(  0) 0) |
| [37] |
Fernández-Macías J C, González-Mille D J, García-Arreola M E, et al. Integrated probabilistic risk assessment in sites contaminated with arsenic and lead by long-term mining liabilities in San Luis Potosi, Mexico[J]. Ecotoxicology and Environmental Safety, 2020, 197: 110568. DOI:10.1016/j.ecoenv.2020.110568
(  0) 0) |
| [38] |
Suter G W, Vermeire T, Munns W R, et al. Framework for the integration of health and ecological risk assessment[J]. Human and Ecological Risk Assessment: An International Journal, 2003, 9(1): 281-301. DOI:10.1080/713609865
(  0) 0) |
| [39] |
Huang L, Ban J, Sun K, et al. The influence of public perception on risk acceptance of the chemical industry and the assistance for risk communication[J]. Safety Science, 2013, 51(1): 232-240. DOI:10.1016/j.ssci.2012.05.018
(  0) 0) |
| [40] |
Morgan G H, Dowlatabadi M, Henrion D, et al. Best practice approaches for characterizing, communicating and incorporating scientific uncertainty in climate decision making: Final report[R]. Washington, D C: United States Climate Change Science Program, 2009.
(  0) 0) |
 2022, Vol. 59
2022, Vol. 59


