2. 中国科学院大学资源与环境学院, 北京 100049
2. Colleage of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China
了解溶质在土壤中的迁移规律对农业生产、资源利用和环境污染防治等具有重要意义,数学模型是描述溶质迁移过程和预测溶质动态分布的有效手段[1-2]。其中,对流-弥散方程(Convection- dispersion equation,CDE)可以体现土壤溶质迁移过程中的对流、弥散等基本机理,是土壤溶质迁移的基本方程[3-4]。其中,溶质迁移参数(如弥散系数D和延迟因子R等)的确定是CDE应用的关键,通过测定溶质穿透曲线并利用CXTFIT软件拟合估算是目前常用做法[5],但该方法是基于最小二乘法实现的,因此获得参数值不唯一。针对这一问题,Shao等[6]利用溶质在多孔介质中迁移锋面的可探测性,提出了求解CDE的边界层方法:以溶质锋作为下边界,并用多项式描述剖面溶质浓度,获取了溶质浓度时空分布的显式解析表达式,以及估算溶质迁移参数的线性拟合方法。基于相同的思路,通过假定溶质剖面分布曲线可用不同函数近似表示,多种边界层解相继被提出[7-12]。该方法适用于研究吸附性溶质在稳定流场饱和土壤中的迁移过程。采用染色示踪或时域反射等方法获取土壤中溶质锋随时间的迁移规律,即可利用边界层方法确定溶质迁移参数,进而估算剖面溶质动态分布。与穿透曲线拟合法相比,该方法可以简单快速地估算溶质迁移参数,且边界层解具有相对简洁的表达形式,用于预测剖面溶质浓度分布时更加直观,而选择一个适宜的边界层解是边界层方法应用的基础和关键。本研究通过比较多项式解、复合解、指数解、对数解和微小通量解在多种参数组合条件下精度随时间的变化以及估算溶质在不同土壤中迁移参数的误差,指出各边界层解的适用范围和优缺点,以期为土壤一维稳态溶质迁移研究中边界层方法的合理选用提供依据。
1 材料与方法 1.1 土柱实验基本信息溶质锋深度随时间变化的实测数据来源于郑纪勇[13]和文红艳[14]开展的垂直土柱易混置换实验,填装土壤分别为安塞黄绵土、杨凌塿土、榆林风沙土和岳麓山红壤,溶质锋深度利用时域反射仪(Time- domain reflectometer,TDR)探测,各土柱基本信息如表 1所示。
|
|
表 1 土柱实验基本设置及基本物理参数 Table 1 Experimental setup and basic physical parameters of soil columns |
稳态流条件下,考虑对流、弥散和线性等温吸附作用时,描述一维溶质迁移的CDE方程可写为[3,15]:
| $ R\frac{{\partial C}}{{\partial t}} = D\frac{{{\partial ^2}C}}{{\partial {x^2}}} - v\frac{{\partial C}}{{\partial x}} $ | (1) |
式中,C为溶质浓度(g·cm–3),R为考虑线性吸附的延迟因子,D为弥散系数(cm2·min–1),v为平均孔隙水流速(cm·min–1),x为剖面深度(cm),t为时间(min)。其中,D与v的比值为弥散度,常用λ表示,即λ=D/v。利用边界层方法求解方程(1)时,实验土体满足van Genuchten和Parker [16]提出的初始和边界条件。
(1)多项式边界层解。在假设溶质浓度剖面分布可以用二次函数近似表示的基础上,Shao等[6]将溶质锋作为下边界层,其深度表达为时间的函数
| $ C\left( {x,t} \right) = \frac{{vd\left( t \right){C_0}}}{{vd\left( t \right) + 2D}}{\left[ {1 - \frac{x}{{d\left( t \right)}}} \right]^2} $ | (2a) |
| $ d\left( t \right) = \frac{{3vt}}{{2R}} + \sqrt {{{\left( {\frac{{3vt}}{{2R}}} \right)}^2} + \frac{{6Dt}}{R}} $ | (2b) |
进一步利用三次函数近似表示浓度剖面,得到三次多项式解为:
| $ C\left( {x,t} \right) = \frac{{vd\left( t \right){C_0}}}{{vd\left( t \right) + 3D}}{\left[ {1 - \frac{x}{{d\left( t \right)}}} \right]^3} $ | (3a) |
| $ d\left( t \right) = \frac{{2vt}}{R} + \sqrt {{{\left( {\frac{{2vt}}{R}} \right)}^2} + \frac{{12Dt}}{R}} $ | (3b) |
通过推求更高阶数方程,Wang等[7]观察到不同边界层解之间的相似性,利用n阶多项式描述剖面溶质浓度,求得了多项式边界层通解。对多项式解精度随阶数n的变化规律进行分析后发现,当n为2或3时对应的多项式边界层解精度最高,在n≥3时,边界层解的精度随n取值增大而降低。
(2)指数边界层解。魏峰和王全九[8]根据指数函数图像特点,提出了描述溶质浓度分布的指数函数模型,并指出该指数边界层解适用于孔隙流速较小的情形,应利用短历时推求相关参数。Tan等[9]在其基础上改进了指数函数模型,得到了新的指数边界层解:
| $ C\left( {x,t} \right) = \frac{{v{C_0}}}{{{{e} ^{ - 1}}vd\left( t \right) + \left( {1 - {e^{ - 1}}} \right)D}} $ | (4a) |
| $ d\left( t \right) = \frac{{vt}}{{\left( {{e} - 2} \right)R}} + \sqrt {{{\left( {\frac{{vt}}{{\left( {{e} - 2} \right)}}} \right)}^2} + \frac{{2\left( {{e} - 1} \right)Dt}}{{\left( {{e} - 2} \right)R}}} $ | (4b) |
通过分析不同情形下指数边界层解的精度发现,指数解在孔隙流速较大、延迟作用较弱时对参数D和R的估算更准确。
(3)复合函数边界层解。为探究指数函数与多项式组合是否具有更高精度,Wang和Shao[10]对比评价了指数函数与不同阶数多项式组合形成的复合函数解,指出由指数项和二阶多项式组成的复合函数解具有较高的精度,其表达式如下:
| $ C\left( {x,t} \right) = \frac{{vC0d\left( t \right)}}{{(3 + {\rm{e}}) + {\rm{e}}vd(t)}}\left[ {\exp \left( {1 - \frac{x}{{d\left( t \right)}}} \right) - 3\frac{x}{{d\left( t \right)}} + 2{{\left( {\frac{x}{{d\left( t \right)}}} \right)}^2}} \right] $ | (5a) |
| $ d\left( t \right) = \frac{{3{\rm{e}}vt}}{{\left( {6\rm{e} - 11} \right)R}} + \sqrt {{{\left( {\frac{{3{\rm{e}}vt}}{{\left( {6\rm{e} - 11} \right)R}}} \right)}^2} + \frac{{6\left( {3 + \rm{e} } \right)Dt}}{{\left( {6\rm{e} - 11} \right)R}}} $ | (5b) |
(4)微小通量解。上述方法的求解条件之一是溶质锋处溶质浓度梯度为0,但这与实际情况可能存在一定差异,因此刘春平和邵明安[11]假设下边界层处存在微小溶质通量δ,利用拉普拉斯变换方法求解了CDE,获得了溶质锋随时间的迁移规律:
| $ D\left( t \right) = \frac{{vt}}{R} + \sqrt {{{\left( {\frac{{vt}}{R}} \right)}^2} + \frac{{4DAt}}{R}} $ | (6a) |
| $ {\rm{A = - ln}}\left( {\frac{{k\sqrt \pi \mathit{vt}/R}}{{2\sqrt {Dt/R} }}} \right) $ | (6b) |
研究发现k取0.001时微小通量解的精度较高。
(5)对数边界层解。同样地,考虑到溶质锋处浓度梯度不为0的情况,Wang等[12]利用对数函数描述溶质浓度分布并推求CDE,由此获得的溶质浓度和溶质锋表达式分别为:
| $ C\left( {x,t} \right) = \frac{{v{C_0}d\left( t \right)}}{{2D + vd\left( t \right)\ln 3}}\ln \left( {\frac{{d\left( t \right)}}{{2x + d\left( t \right)}}} \right) $ | (7a) |
| $ d\left( t \right) = \frac{{vt\ln 3}}{{\left( {2 - \ln 3} \right)R}} + \sqrt {{{\left( {\frac{{vt\ln 3}}{{\left( {2 - \ln 3} \right)R}}} \right)}^2} + \frac{{4Dt}}{{\left( {2 - \ln 3} \right)R}}} $ | (7b) |
利用相对均方根误差(Relative root mean square error,RRMSE)评价各边界层解在预测溶质浓度剖面,其计算方法如下:
| $ RRMSE = \frac{{\sqrt {{{\sum\limits_{i = 1}^n {{{\left( {{{\hat C}_i} - {C_i}} \right)}^2}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^n {{{\left( {{{\hat C}_i} - {C_i}} \right)}^2}} } n}} \right. } n}} }}{{{{\sum {{{\hat C}_i}} } \mathord{\left/ {\vphantom {{\sum {{{\hat C}_i}} } n}} \right. } n}}} $ | (8) |
式中,
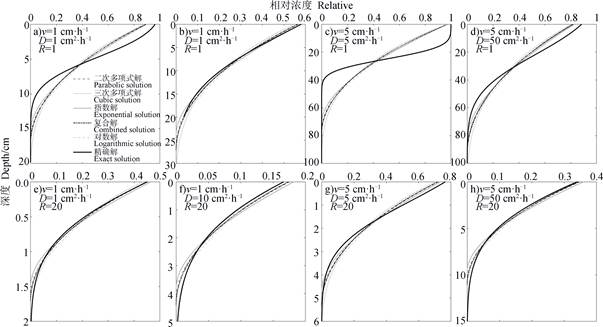
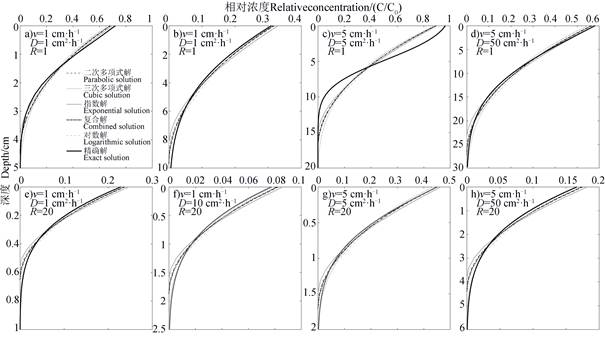
不同边界层解是基于不同的剖面浓度分布假设所获得的,其预测精度之间存在一定的差异。本研究依据文献中的室内及田间观测数据,分别以v = 1和5 cm·h–1,λ = 1和10 cm以及R = 1和20为例,对比分析由各边界层解计算得到的剖面溶质分布与精确解的差异。一般而言,室内扰动土柱的弥散度为0.5~2 cm[17-18],田间试验获得的弥散度数值为5~20 cm[19-20],弥散度往往随运移距离或土柱尺度增大而增加,但该现象对室内填装土柱则不存在[19]。由图可知,各边界层解预测的浓度分布曲线在多数情形下十分接近精确解,且不同边界层解之间差异并不明显(图 1和图 2),但边界层方法对应的溶质锋深度普遍小于精确解。在t = 1 h和5 h条件下,精确解和边界层解浓度分布曲线的差异均在v = 5 cm·h–1,D = 5 cm2·h–1,R = 1时(图 1c和图 2c)时最大,t = 5 h时图 2a(v = 1 cm·h–1,D = 1 cm2·h–1,R = 1)和图 2d(v = 5 cm·h–1,D = 50 cm2·h–1,R = 1)中也能明显看到精确解与边界层的差异。对比各参数条件下由不同边界层解获得的溶质分布曲线可以发现,指数解对剖面上部浓度的预测值高于其他边界层解,但预测剖面下部溶质浓度值则最低;同时可以看到三次多项式解对剖面下部溶质浓度的预测值最高。
|
图 1 边界层解和精确解方法预测1 h溶质浓度剖面对比 Fig. 1 Comparison between concentration profiles obtained from boundary layer and exact solution at 1 h |
|
图 2 边界层解和精确解方法预测5 h溶质浓度剖面对比 Fig. 2 Comparison between concentration profiles obtained from boundary layer and exact solution at 5 h |
上述结果表明,边界层解可以用于预测溶质在土壤中的迁移过程和动态分布,但在水流流速较快的情形下精度相对较低,此时溶质主要发生对流运移,由此可知边界层解更适用于弥散作用为主要机制的情形,因此应尽量在溶质流速慢、弥散作用或溶质吸附性较强时选用。这主要因为由多项式函数、指数函数、复合函数以及对数函数获得的溶质浓度剖面分布始终呈现浓度变化率随深度增加而不断减小的趋势,而当平均孔隙水流速大、溶质不被土壤颗粒吸附且弥散作用较弱时,溶质浓度变化在初始阶段表现为随深度增加而不断减小,但剖面上层溶质累积迅速,经过较短时间后溶质浓度变化率就出现随深度先增大后减小的现象,边界层方法中假设的浓度分布曲线难以准确描述此时的溶质分布,因此由边界层方法获取的浓度分布与实际情况存在较大差异。此外,由于填装均质土柱弥散度通常较小,因而在水流流速小的情形下使用边界层解更可能得到准确的结果;田间试验条件下边界层解用于较大尺度土体研究的精度相对更高。
为进一步了解边界层解精度在不同参数条件下的变化规律,表 2列举了图 1和图 2对应参数条件下各边界层解的预测误差。由表可知,各边界层解在预测1 h的溶质分布时均具有较高精度,除v = 5 cm·h–1、D = 5 cm2·h–1、R = 1情形外,误差均小于0.2,证实了边界层解可用于预测较短时间内剖面溶质浓度分布的可靠性。边界层解对5 h溶质浓度的预测误差多数情况下大于1 h,但在延迟因子和弥散度均较大时,边界层解在5 h的预测误差反而低于1 h。对比图 1和图 2也可看出,图g和图h中边界层解与精确解获得的溶质浓度剖面十分接近。各边界层解的精度是由v、D和R共同决定的,对其中单个参数变化的响应规律较为复杂。流速变化对边界层解精度影响最大,当流速由1 cm·h–1增大至5 cm·h–1时,多项式解、指数解和复合解描述非吸附性溶质迁移过程的误差甚至扩大了2倍以上,但对于吸附性较强的溶质迁移过程而言,流速的影响相对较小。溶质弥散作用所占比重增加时,边界层解精度通常会有所提高,尤其是在溶质吸附性较弱的条件下,然而当R远大于1时,λ增大也可能导致边界层解的预测误差变大,但λ改变对边界层解精度产生的影响总体上小于v。结合图 1和图 2可知,λ增加会导致相同时间内溶质迁移距离变长、同一深度的溶质浓度变低,边界层解和精确解描述非吸附性溶质迁移过程的差异减小,且5 h较1 h更明显;而当溶质被多孔介质吸附时,边界层解在描述弥散为主要机制的溶质迁移过程时精度可能更高。对比v和λ相同条件下利用边界层解模拟吸附性和非吸附性溶质分布结果可知,多数情况下边界层解用于吸附性溶质迁移过程的预测时较非吸附性溶质具有更高的精度。当v和D一定时,R从1增大至20后,边界层解的预测误差平均降低了14.21%,但对于v=1 cm、D=10 cm2·h–1的情形,预测误差反而增加。综上,利用边界层方法解决溶质迁移问题时应综合考虑溶质迁移机制及吸附特性,溶质弥散作用较强时边界层解的精度通常较高,溶质以对流迁移为主时应进一步考虑溶质吸附特性。
|
|
表 2 不同参数条件下边界层解预测浓度剖面的相对均方根误差(RRMSE) Table 2 The relative root mean square errors of boundary layer solutions for predicting concentration profiles under different conditions |
不同参数条件下各边界层解的精度存在差异,在表 2所示情形中,复合解的预测误差总和最小,但最优预测结果多由三次多项式解或指数解取得。利用不同边界层解计算1 h浓度分布时,总体来看三次多项式解得到的结果最佳,且对吸附性溶质的预测精度相对更高;指数解在预测5 h剖面溶质分布时整体上优于其他边界层解,其精度在R=1的情形下高于R=20。由上述对比分析可知,利用边界层方法计算较短时间内的溶质剖面分布时,对于吸附性溶质而言,可选用三次多项式边界层解,而当溶质不被吸附时,则可选用指数解或二次多项式解;而预测较长时间后的溶质浓度时,采用指数解获取的非吸附性溶质浓度分布更接近实际分布,三次多项式解和复合解可用于计算吸附性溶质的分布情况。
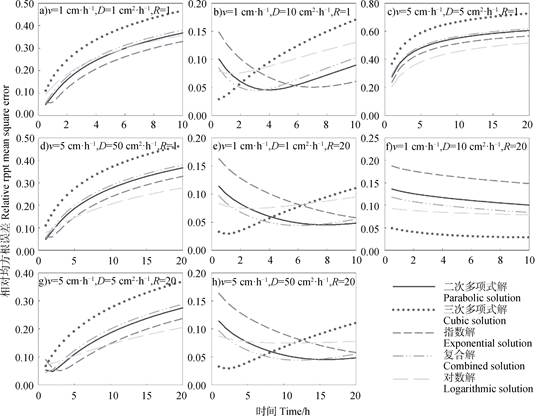
2.2 不同边界层解预测浓度剖面精度随时间的变化边界层解对溶质迁移过程不同阶段剖面溶质分布的预测精度是不同的,为进一步掌握各边界层解精度的变化规律,本文分析了各边界层解对剖面溶质分布的预测误差随时间的变化,结果见图 3。从图中可以看出,图 3e(v=5 cm·h–1,D=5 cm2·h–1,R=1)情形下边界层解的预测误差最大,其预测2 h的剖面浓度误差均已超过30%,远高于其他参数情形下产生的误差,而当v和λ一定时,R=20时边界层解的误差总体小于R=1,表明边界层方法更适宜于描述具有较强吸附性溶质的迁移过程。
|
图 3 各边界层解预测浓度剖面的相对均方根误差随时间变化 Fig. 3 Variation of RRMSE of boundary layer solutions with time on predicting solute concentration profiles under different conditions |
对比边界层解和精确解的浓度表达式可知,在溶质迁移进行较长时间后,由边界层方法计算得到的剖面浓度分布与实际情况将存在很大误差,因此利用该方法预测剖面溶质浓度和估算溶质迁移参数时,选取适宜的边界层解和测定时长对于准确获取结果起着关键作用。在图 3中,λ=1且R=1时(图 3a和图 3e)所有边界层解误差随时间推移始终表现出增加的趋势,其中三次多项式解的误差明显高于其他边界层解,指数解的误差最小,二次多项式解、复合解和对数解之间差异不大。在平均孔隙水流速快的条件下,λ或者R较大时,二次多项式解、指数解和复合解可能在初始阶段有所减小,但短时间后即快速增大,该情形下可以选用二次多项式解或复合解预测溶质迁移初期的浓度分布。对于吸附性较强的溶质而言,多数情况下其迁移过程均可用边界层方法较为准确地进行描述,随迁移过程的进行,边界层解的预测误差基本呈现先减小后增大的趋势,而v=1 cm·h–1、D=10 cm2·h–1、R=20(图 3d)条件下,除三次多项式解外,各边界层解精度在0~20 h内逐渐提高,此时利用复合解或二次多项式计算得到的溶质分布相对更加准确。综合以上对比分析,各边界层解精度随时间推移总体呈现降低趋势,边界层解描述溶质迁移过程早期阶段时更加准确,随着时间的推移,由于溶质实际剖面分布与假设之间差异逐渐增加,边界层解的预测精度越来越低,溶质流速慢和吸附性强情况下边界层解可在相对较长时间内具有较小预测误差,因此利用边界层方法预测溶质剖面浓度时应尽量控制实验时长。选择边界层方法时,对于非吸附性溶质可优先使用指数解;对于吸附性溶质而言,当v快且λ较小时也可使用指数解,其他情况下二次多项式解或复合解的预测结果更优。
2.3 不同边界层解估算溶质迁移参数的对比分别利用各边界层解对黄绵土、塿土、风沙土、红壤等4种不同土壤在土柱实验中的溶质迁移参数进行估算,结果见表 3。利用指数解估算红壤的溶质迁移参数时,对校正后的d2(t)/t与d(t)数据进行拟合后得到的截距小于0,无法计算D。由表可知,边界层解估算R的准确度高于D,且不同边界层解之间获得的R值十分近似,D值差异相对较大。多项式解、指数解、复合解和对数解对黄绵土、塿土和风沙土中R的估算值相同,与CXTFIT拟合值也十分接近,误差为0.86%~30.67%,而微小通量解的估算值明显小于其他边界层解,在风沙土和红壤中的计算结果最优。利用除微小通量解外的其他边界层方法计算溶质迁移参数时,获得的溶质锋深度小于根据微小通量法确定的深度,因而计算得到的R值偏小。对比不同边界层解与CXTFIT获得的D值可知,边界层解对D的估算值在黄绵土、塿土和风沙土中大于CXTFIT,在红壤中则相反,微小通量解对D的拟合均小于CXTFIT拟合值。三次多项式解对黄绵土、塿土和风沙土D的估算误差最小,分别为41.22%、327.21%和88.52%,其次为对数解,利用对数解计算得到的结果与三次多项式解十分近似;微小通量解对溶质在红壤中弥散系数D的估算最准确,仅较CXTFIT拟合值低19.35%。估算溶质迁移参数是边界层方法的重要应用之一,但通过边界层方法和穿透曲线拟合法获取的参数值存在差异,一方面是由于边界层解本身是一个近似解,另一方面可能是溶质锋测定过程中产生的误差。染色示踪法和TDR是探测溶质锋的有效手段,通常染色剂的迁移速率小于目标溶质,而TDR也只有当溶质浓度变化达到灵敏度才会产生响应,因此溶质锋实际深度往往大于测定深度[9],导致利用边界层方法估算R和D数值通常偏高。相比之下,TDR探测的溶质锋深度较染色剂指示的结果更加准确。选择精度高的探测仪器可减小溶质锋测定误差,有利于提高边界层解估算溶质运移参数的准确性,但仍需结合仪器的测定精度对边界层测定数据进行修正。此外,结合边界层解精度随时间的变化规律,建议在运用边界层方法计算溶质迁移参数时,尽量测定较短时间内的溶质锋运动过程,并优先选择三次多项式解或对数解。
|
|
表 3 不同边界层解方法获得的溶质迁移参数 Table 3 Solute transport parameters estimated by different boundary layer solutions |
基于CXTFIT拟合获得的参数,分别利用不同边界层解计算下边界层深度并与精确解结果进行比较分析,各边界层解的相对误差如图 4。由图可知,微小通量法对下边界层的估算值均大于实际值,其他边界层解在风沙土、黄绵土和塿土中的估算值初期小于实际值,但随时间推移呈现出逐渐接近而后大于实际值的趋势。其中,三次多项式解对溶质锋深度的计算值显著高于其他边界层解,对数解的计算值最小,其差异主要与函数本身特性有关。进一步对比边界层解用于不同土壤的计算误差发现,边界层解下边界层描述的准确性由高到低依次为:风沙土、黄绵土、塿土、红壤,而边界层解对溶质在黄绵土和风沙土中迁移参数的估算值也最接近精确解。根据土柱实验结果,红壤中溶质迁移的v较大而D较小,溶质以对流迁移为主;黄绵土和风沙土的λ显著高于其他两种土壤,表明溶质的扩散作用相对较强。上述结果表明,边界层解用于描述流速小、扩散强的土壤溶质运移过程时对下边界层的描述更加准确。土壤质地显著影响土壤的孔隙性、持水性和物理机械性质,进而影响溶质在土壤中的迁移过程[21]。通常,质地较细土壤的颗粒具有较强吸附性,运移溶液的流速也较小,边界层解对应的溶质锋深度更加接近精确解,由此估算得到的溶质运移参数也更为准确。

|
图 4 边界层解计算溶质锋深度的相对误差 Fig. 4 Relative error of boundary layer solutions in determining the solute front depth |
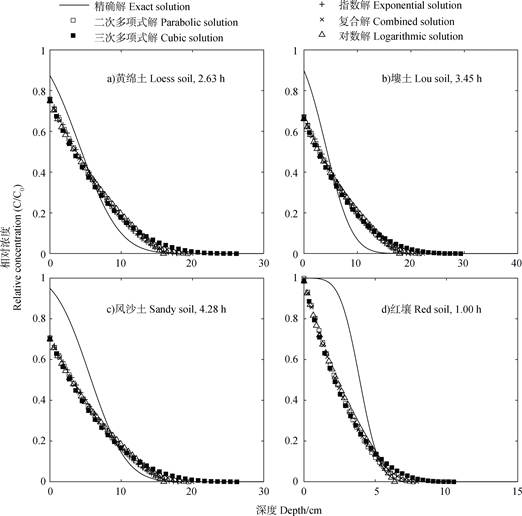
图 5显示了分别利用CXTFIT拟合和边界层方法估算参数绘制的不同土壤剖面Cl–浓度分布曲线。各边界层解浓度剖面与精确解浓度剖面存在一定差异,其中红壤最为显著,边界层方法对剖面上层Cl–浓度预测值偏低,对下层预测值偏高,不同边界层方法之间差异不大。在图中所示时刻,各土壤剖面表层的溶质浓度已接近或达到了C0,且溶质浓度变化率并未随深度增加而持续减小,根据3.1部分的分析可知,边界层方法仅在描述溶质迁移早期,即溶质浓度变化率随深度减小的阶段具有较高精度。但对于图 5所示情况,边界层方法本身已经与精确解方法存在较大差异,这可能是导致边界层方法估算参数误差较大的主要原因。其中,边界层解和精确解在黄绵土2.63 h的溶质分布曲线最接近,与表 2的结果一致,该情形下边界层解对参数的估算结果也最接近CXTFIT拟合数值。Cl–在红壤土柱中迁移时流速快且弥散度小,1 h时在表层约1 cm的土壤中溶质浓度已经达到了C0,边界层方法所利用的函数模型难以准确描述此时的溶质分布,因而由各边界层解估算的溶质迁移参数误差较大。
|
图 5 精确解和溶质浓度剖面对比 Fig. 5 Comparison of solute concentration profiles obtained by the boundary layer and exact solutions |
边界层方法能够准确描述早期的溶质剖面分布情况,但不适宜用于研究以对流迁移为主的溶质迁移过程,即溶质流速较大、弥散作用和吸附性均较弱的情形。利用边界层解计算短历时内的溶质浓度剖面分布时,多数情况下可优先选择三次多项式解,流速快且弥散作用弱的情形选用指数解或复合解最优,计算剖面上部溶质浓度分布时可选用对数解。边界层解能够更加准确地估算延迟因子,且不同边界层解获得的延迟因子数值近似,估算弥散系数时应选用三次多项式解和对数解。溶质锋深度测量误差是边界层方法误差产生的主要原因之一,因此测定时应尽量选用检测灵敏度较高的仪器或对测定深度进行校正。
| [1] |
Li B G, Hu K L, Huang Y F, et al. Advances in modeling and applications of soil solute transport (In Chinese)[J]. Soils, 2005, 37(4): 345-352. DOI:10.3321/j.issn:0253-9829.2005.04.001 [土壤溶质运移模型的研究及应用[J]. 土壤, 2005, 37(4): 345-352.]
(  0) 0) |
| [2] |
Ma D H, Wang Q J. Analysis of two-region model and two-flow domain model for soil solute transport (In Chinese)[J]. Journal of Hydraulic Engineering, 2004, 35(6): 92-97. DOI:10.3321/j.issn:0559-9350.2004.06.016 [土壤溶质迁移的两区模型与两流区模型对比分析[J]. 水利学报, 2004, 35(6): 92-97.]
(  0) 0) |
| [3] |
Parker J C, van Genuchten M T. Flux-averaged and volume-averaged concentrations in continuum approaches to solute transport[J]. Water Resources Research, 1984, 20(7): 866-872. DOI:10.1029/WR020i007p00866
(  0) 0) |
| [4] |
Yan Y F, Li X P, Zhang J B, et al. Parameter estimation and uncertainty evaluation of a soil solute transport model using GLUE (In Chinese)[J]. Acta Pedologica Sinica, 2018, 55(5): 1108-1119. [基于GLUE的土壤溶质运移参数反演及不确定性[J]. 土壤学报, 2018, 55(5): 1108-1119.]
(  0) 0) |
| [5] |
Toride N, Leij F, van Genuchten M T. The cxtfit code for estimating transport parameters from laboratory or filed tracer experiments[J]. US Salinity Laboratory Riverside, 1995.
(  0) 0) |
| [6] |
Shao M, Horton R, Miller R K. An approximate solution to the convection-dispersion equation of solute transport in soil[J]. Soil Science, 1998, 163(5): 339-345. DOI:10.1097/00010694-199805000-00001
(  0) 0) |
| [7] |
Wang J, Shao M A, Huang L M, et al. A general polynomial solution to convection-dispersion equation using boundary layer theory[J]. Journal of Earth System Science, 2017, 126(3): 1-12.
(  0) 0) |
| [8] |
Wei F, Wang Q J. Exponential function model of soil solute transport (In Chinese)[J]. Research of Soil and Water Conservation, 2012, 19(5): 230-234. [土壤溶质迁移的指数函数模型[J]. 水土保持研究, 2012, 19(5): 230-234.]
(  0) 0) |
| [9] |
Tan S, Wang Q J, Zhou B B. An exponential boundary-layer solution to the convection-dispersion equation of solute transport in soils[J]. Canadian Journal of Soil Science, 2017, 97(2): 200-214.
(  0) 0) |
| [10] |
Wang J, Shao M G. Using boundary-layer theory to solve the convection-dispersion equation of solute transport[J]. Canadian Journal of Soil Science, 2017, 97(2): 141-148.
(  0) 0) |
| [11] |
Liu C P, Shao M A. The boundary layer movement of solute transport in soil (In Chinese)[J]. Journal of Hydraulic Engineering, 1999, 30(12): 11-16. DOI:10.3321/j.issn:0559-9350.1999.12.003 [土壤溶质运移的边界层运动[J]. 水利学报, 1999, 30(12): 11-16.]
(  0) 0) |
| [12] |
Wang J, Ji H Y, Shao M G. Evaluation of a logarithmic solution to the convection-dispersion equation obtained from boundary-layer theory[J]. Canadian Journal of Soil Science, 2018, 98(1): 45-54.
(  0) 0) |
| [13] |
郑纪勇. 土壤中溶质运移的边界层方法[D]. 陕西杨凌: 西北农林科技大学, 2001. Zheng J Y. Boundary layer method for solute transport in soils[D]. Yangling, Shaanxi: Northwest A & F University, 2001 (  0) 0) |
| [14] |
文红艳. 土壤溶质锋运移及参数估计的实验研究[D]. 长沙: 湖南师范大学, 2005. Wen H Y. An experimental study on solute front transport in soil and parameter estimate[D]. Changsha: Hunan Normal University, 2005 (  0) 0) |
| [15] |
Gao G Y, Feng S Y, Huang G H. Simulation of solute transport at large scale in saturated heterogeneous soil with two-region model (In Chinese)[J]. Acta Pedologica Sinica, 2008, 45(3): 398-404. DOI:10.3321/j.issn:0564-3929.2008.03.003 [饱和非均质土壤中溶质大尺度运移的两区模型模拟[J]. 土壤学报, 2008, 45(3): 398-404.]
(  0) 0) |
| [16] |
van Genuchten M T, Parker J C. Boundary conditions for displacement experiments through short laboratory soil columns[J]. Soil Science Society of America Journal, 1984, 48(4): 703-708. DOI:10.2136/sssaj1984.03615995004800040002x
(  0) 0) |
| [17] |
Fried J J. Groundwater pollution - Theory, methodology, modelling and practical rules[M]. Amsterdam: Elsevier, 1975.
(  0) 0) |
| [18] |
Freeze R A, Cherry J A. Groundwater . Englewood Cliffs, NJ: Prentice-Hall, 1979.
(  0) 0) |
| [19] |
Jury W A, Gardner W R, Gardner W H. Soil physics[M]. John Wiley, 1991.
(  0) 0) |
| [20] |
Perfect E, Sukop M C, Haszler G R. Prediction of dispersivity for undisturbed soil columns from water retention parameters[J]. Soil Science Society of America Journal, 2002, 66(3): 696-701. DOI:10.2136/sssaj2002.6960
(  0) 0) |
| [21] |
Wang Y, Liu J, Wang Y Q. Effects of soil physical properties on nutrient transport velocity in Loess Plateau (In Chinese)[J]. Bulletin of Soil and Water Conservation, 2005, 25(4): 20-23. DOI:10.3969/j.issn.1000-288X.2005.04.005 [黄土高原土壤物理性质对养分迁移速率的影响[J]. 水土保持通报, 2005, 25(4): 20-23.]
(  0) 0) |
 2022, Vol. 59
2022, Vol. 59


