2. 中国科学院水利部水土保持研究所/西北农林科技大学黄土高原土壤侵蚀与旱地农业国家重点实验室, 陕西杨凌 712100
2. Institute of Soil and Water Conservation, Chinese Academy of Sciences and Ministry of Water Resources/State Key Laboratory of Soil Erosion and Dryland Agriculture on the Loess Plateau, Northwest A & F University, Yangling, Shaanxi 712100, China
离子在土壤矿物表面的交换吸附作用是影响其在土壤环境中的迁移、转化及生物有效性的重要过程。根据电中性法则,当土壤矿物表面的离子交换吸附达到理想平衡状态时,用于补偿表面净电荷的吸附态反离子将被其他交换离子完全取代,取代离子的平衡吸附量等于土壤矿物的阳离子交换量[1]。然而诸多研究[2-4]证实,实验条件下离子的平衡吸附量普遍小于土壤/黏土矿物的阳离子交换量,理想的离子吸附平衡不易实现。
现有理论认为,带电颗粒表面离子非理想交换吸附的发生与土壤矿物的层间固定[5]、离子与吸附位点空间尺寸的不相容性[6]等因素导致的交换离子扩散受阻密切相关。潘纲[7]提出的亚稳平衡态吸附理论更广泛地认为,吸附态分子一般是以不同能量的亚稳平衡态结合在固体表面,而实际离子吸附反应的平衡特性取决于其亚稳平衡吸附态。Luo等[8]利用密度泛函理论和X射线吸收精细结构研究发现,金属离子吸附解吸中存在的亚稳态机制主要源于弱静电力的控制。静电力是土壤矿物颗粒与带电离子间重要的相互作用力,在离子交换吸附过程中扮演着十分重要的角色。若离子-表面相互作用仅受静电力支配,则不同种类同价离子的亚稳平衡吸附特征可能相同。但是近期研究[9-10]发现,即便是不同类型的同价碱金属离子,它们在土壤矿物表面的亚稳平衡吸附特征迥异。说明除静电力外,离子水化、诱导力和色散力等可能亦对离子-表面相互作用有重要影响[9]。
在水溶液中,胶体粒子通常具有丰富的表面电荷,与扩散分布的吸附态反离子可在粒子表面附近产生高达108~109 V·m−1的电场,反离子的吸附过程必然受到强电场的深刻影响[11-12]。基于古伊-查普曼(Gouy-Chapman)理论研究表明,强大的外部电场可从根本上改变阳离子非价电子的能量状态,导致离子的强极化效应,使离子与带电表面间产生新的相互作用[13-15]。研究发现,强极化作用引起的离子-表面间相互作用强度甚至超过了经典的库仑相互作用[4,10]。因此,这种离子-表面间新的相互作用力可能在离子交换吸附的亚稳平衡及其特异性效应中起着至关重要的作用。本研究通过开展不同离子浓度条件下钾离子(K+)、钠离子(Na+)、锂离子(Li+)三种碱金属离子在蒙脱石表面的吸附动力学实验,旨在阐明离子交换吸附的亚稳平衡及其特异性效应的发生机制。
1 材料与方法 1.1 供试材料组成与性质本研究选用蒙脱石(内蒙古物华天宝矿物资源有限公司)为供试原材料,其X射线衍射(XRD,Ultima IV型,理学,日本)图谱如图 1所示,该样品的矿物组成中蒙脱石和石英的含量分别为980 g·kg−1和20 g·kg−1。利用X射线荧光光谱(Axios PW4400型,帕纳科,荷兰)和物质表面性质联合测定法[16-17]分别测定了蒙脱石样品的化学组成和表面性质,结果如表 1所示。

|
图 1 蒙脱石样品的X射线衍射图谱 Fig. 1 The X-ray diffraction pattern of the montmorillonite sample |
|
|
表 1 蒙脱石样品的化学组分和表面性质 Table 1 The chemical composition and surface properties of the montmorillonite sample |
为纯化供试蒙脱石表面离子组成,将其制备成硝酸铯(CsNO3)饱和样。取100 mmol·L−1 CsNO3电解液500 mL,与50 g蒙脱石原料混合后转移至1 000 mL三角瓶,在220 r·min–1条件下连续恒温振荡24 h,离心后弃去上清液。向沉淀物中再次加入等浓度等体积的CsNO3电解液,以上处理共计重复三次。用等体积的超纯水代替CsNO3电解液,重复上述步骤多次,最终用原子吸收光谱仪(Z-2000,日立)测定上清液中Cs+离子浓度,直至洗去蒙脱石表面过剩的Cs+。最后,样品在70℃条件下烘干后过60目筛备用。
1.3 离子吸附动力学实验采用混合恒流置换方法[4]开展离子吸附动力学实验。为探究碱金属离子的亚稳平衡吸附过程,选取K+、Na+、Li+作为指示离子,伴离子选择NO3−,设置离子浓度为0.1和10 mmol·L−1,实验温度25 ℃。称取约0.5 g蒙脱石Cs+-饱和样,将其与少量超纯水混合后用胶头滴管逐滴加入交换柱,使悬液尽可能均匀地平铺于垫有滤纸的交换室中,期间用恒流泵(HL-2,上海沪西)匀速抽滤出悬液中的水分。再次设置适宜的恒流泵转速,使不同类型、不同浓度条件的交换液以0.5 mL·min−1的恒定流速穿过静置交换柱中平铺的蒙脱石样品,用自动部分收集器(DBS-100,上海沪西)收集流出液。由于离子交换时间与其浓度成反比,因此将0.1和10 mmol·L−1的电解液对应条件下的流出液收集时间设置为20和5 min。利用实验前后各试管质量差(流出液密度近似为1 g·cm−3)得到各实验条件下的交换液体积,火焰光度计(AP1401型,上海傲谱)测定流出液中K+、Na+、Li+浓度,并对交换柱内土样烘干后称重,通过计算最终得到不同实验条件下各碱金属离子在蒙脱石表面的吸附量。
1.4 数据处理已有研究表明,离子在矿物表面的静电吸附或交换吸附过程实质是离子在带电颗粒表面静电场作用下的扩散过程[18]。因此基于静电场理论的适用条件,阳离子吸附将遵守两类速率方程:
当离子-表面间存在强吸附力时,离子的表观平均吸附速率可用零级速率方程表示[19-20]:
| $ \frac{{d{N_\rm{X}}(t)}}{{dt}} = {k_{\rm{X}(0)}}{N_\rm{X}}{(t)^0} $ | (1) |
式(1)中,NX(t)为X+离子在t时刻的吸附量,mmol·kg−1;kX(0)为零级速率常数,mmol·kg−1·min−1。
当离子-表面间的强吸附力作用饱和而转向弱吸附力,或仅存在弱吸附力时,离子的表观平均吸附速率可用一级速率方程表示[21]:
| $ \frac{{d{N_\rm{X}}(t)}}{{dt}} = {k_{\rm{X}(1)}}\left[ {1 - \frac{{{N_\rm{X}}(t)}}{{{N_\rm{X}}(t \to \infty )}}} \right] $ | (2) |
式(2)中,NX(t→∞)为离子X+在t→∞时的平衡吸附量,mmol·kg−1;kX(1)为一级速率常数,mmol·kg−1·min−1。
利用上述模型结合Microsoft Excel 2016处理数据,并用Origin 2021作图。
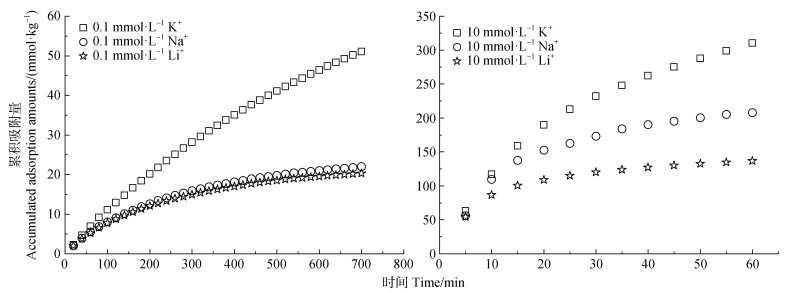
2 结果 2.1 蒙脱石表面碱金属离子的累积吸附特征基于恒流实验的测定,X+/Cs+交换体系中碱金属X+(X+ = K+、Na+、Li+)在不同离子浓度条件下的累积吸附量随时间的变化如图 2所示。由图 2可知,在相同离子浓度条件下,三种碱金属离子在同一时间内的累积吸附量表现为:Li+ < Na+ < K+。例如,在离子浓度为0.1 mmol·L−1时,600 min时间内,Li+、Na+和K+的累积吸附量分别为19.50、21.01和46.36 mmol·kg−1;当离子浓度升至10 mmol·L−1时,60 min时间内,Li+、Na+和K+的累积吸附量分别为136.7、207.8和310.1 mmol·kg−1。同一时段内三种离子的累积吸附量呈现出差异性。尽管Li+、Na+、K+的累积吸附量随着离子浓度增加而增加,但实验条件下三种碱金属离子的吸附量均远小于蒙脱石的表面电荷数量。以上结果表明:(1)有限时间内Li+、Na+、K+在Cs+-蒙脱石表面不能达到理想的吸附平衡;(2)碱金属离子的非理想吸附受离子浓度和离子特异性效应的共同影响。
|
图 2 Li+、Na+、K+在Cs+-蒙脱石表面的累积吸附量随时间的变化 Fig. 2 Changes in time of cumulative adsorption amounts for Li+, Na+, and K+ at the surface of Cs+- montmorillonite |
为进一步探明碱金属离子非理想吸附对其吸附动力学过程的影响,引入考虑土壤表面电场的离子吸附动力学模型[18]。利用图 2碱金属离子累积吸附量与时间的关系,将式(1)和(2)中的微分转化为差分dNX(t)/dt ≈ [NX(tm+1)−NX(tm)]/(tm+1−tm)和NX(t)≈ NX(tm+1/2)= NX(tm)+0.5[NX(tm+1)−NX(tm)] [18-22],其中m=1,2,3,…...可得到dNX(t)/dt vs. NX(t)间的关系,如图 3所示。

|
图 3 不同浓度Li+、Na+、K+在Cs+-蒙脱石表面的吸附动力学曲线 Fig. 3 Adsorption kinetics curves for different concentrations of Li+, Na+, and K+ at the surface of Cs+- montmorillonite |
图 3表明:(1)供试条件下Cs+-蒙脱石表面不同浓度Li+、Na+、K+的吸附动力学曲线均仅表现出一级动力学特征,说明离子-表面间存在弱力吸附作用;(2)相同离子浓度条件下三种碱金属离子在Cs+-蒙脱石表面的吸附速率常数和平衡吸附量均表现为:Li+ < Na+ < K+,同一离子的吸附速率及平衡吸附量随着离子浓度的增加而增加。如表 2所示,离子浓度为0.1 mmol·L−1时,Li+、Na+、K+在蒙脱石表面的吸附速率分别为0.080 35、0.083 41、0.114 2 mmol·kg−1·min−1,平衡吸附量分别为21.71、23.74、80.33 mmol·kg−1;当离子浓度增至10 mmol·L−1时,Li+、Na+、K+在蒙脱石表面的吸附速率分别为10.52、15.16、13.21 mmol·kg−1·min−1,平衡吸附量分别为126.2、178.9、309.8 mmol·kg−1。恒流法用于X+/Cs+交换体系中X+(X+ = K+、Na+和Li+)的吸附研究,X+在平衡时的吸附量不受阳离子交换平衡的限制[19]。因为所有的吸附态Cs+将在t→∞时被K+、Na+或Li+交换,K+、Na+或Li+的吸附量等于表面电荷数量。考虑到样品表面电荷为1 150 mmol(−)·kg−1,理论上K+、Na+或Li+在t→∞时的吸附量等于1 150 mmol·kg−1。然而以上结果说明:t→∞时各碱金属离子的平衡吸附量均小于蒙脱石的阳离子交换量(表面负电荷数量),此时各离子处于非理想的亚稳平衡态而非理想的饱和吸附平衡状态。
|
|
表 2 离子吸附速率常数和平衡吸附量 Table 2 Ion adsorption rate constant and equilibrium adsorption amounts |
目前研究认为,离子出现亚稳平衡吸附的原因为:离子以不同微观结构在形貌异质性表面的附着[7],离子在黏土矿物边缘、夹层或磨损边缘坍塌处发生的缓慢迁移[23-24],离子尺寸与吸附剂表面特定位点可用空间的不相容性[25],外部不充分扰动导致的交换离子扩散受阻[26]。虽然上述观点从不同角度阐述了离子亚稳平衡吸附的可能影响因素,但系统地从理论上对离子亚稳平衡吸附产生原因的解析尚较缺乏。并且,以上影响因素依然不能解释,为何K+、Na+、Li+在Cs+-蒙脱石表面表现出的亚稳平衡吸附特征与离子浓度和离子特异性效应密切关联。Li等[18]研究认为,离子交换吸附的本质是两种离子在双电层和本体溶液之间的相互扩散。基于此,离子亚稳平衡吸附的产生可能是由离子扩散的能量势垒(或活化能)造成的。因为离子交换吸附中体系的高活化能易造成离子交换过程出现低动力学速率,进一步导致离子的亚稳平衡吸附。实验结果表明,Li+、Na+、K+在Cs+-蒙脱石表面的吸附亚稳平衡态存在明显的离子特异性效应。例如,在阳离子浓度为10 mmol·L−1时,Li+、Na+、K+在t→∞时的吸附量分别仅占真正平衡时吸附量的10.97%、15.56%、26.94%(表 2)。因此,离子特异性效应深刻影响着阳离子吸附/解吸的困难程度。如何解释并描述离子特异性效应对亚稳态的影响,以及特异性效应与不同体系活化能的关联?为了回答该问题,接下来将进行更深入的讨论分析。需要注意的是,本研究基于以下适用条件拟建立描述离子的亚稳平衡吸附及其特异性效应的理论模型:(1)胶体双电层理论可描述黏土中的离子交换吸附[19];(2)阳离子在黏土中的扩散和吸附受扩散层中源自表面电荷的电场影响[18];(3)在由恒流混合置换实验控制的初始和边界条件下,通过解斯莫鲁霍夫斯基(Smoluchowski)方程得到的动力学模型(式(1)和式(2))可适用于本研究[20,22]。
3.1 不存在极化效应时离子亚稳平衡吸附的理论分析当考虑黏土矿物表面的静电场时,对于利用恒流实验开展的X+/Cs+交换中X+(X+ = K+、Na+和Li+)的吸附,t时间内X+从本体溶液至扩散双电层中的扩散通量为[9,18,20]:
| $ \frac{{d{N_\rm{X}}(t)}}{{dt}} = \frac{{{\pi ^2}{D_\rm{X}}}}{{4{l^2}}}\left[ {S{f_{0(\rm{X})}}\int_0^l {{e^{ - \frac{{{Z_X}F\varphi (x)}}{{RT}}}}} dx - S\int_0^l {{f_\rm{X}}(x,t)dx} } \right] $ | (3) |
式(3)中,φ(x)为距离颗粒表面x位置处的电位,mV;π为圆周率;DX为离子的扩散系数;ZX为X+离子的化合价,此处ZX = 1;l为扩散层外层X+/Cs+交换发生的深度,nm;S为样品的比表面积,m2·g−1;f0(X)为本体溶液中X的浓度,mol·L−1;fX(x,t)为X+在位置x处t时刻的浓度,mol·L−1;F为法拉第常数;R为标准气体常数;T为绝对温度,K。
电场力驱动下的离子吸附过程中,其吸附量可表达为:
| $ {N_\rm{X}}(t) = S\int_0^l {{f_\rm{X}}(x,t)} dx $ | (4) |
在t→∞的平衡态时,离子分布服从玻尔兹曼(Boltzmann)函数:
| $ {f_\rm{X}}(x,\infty ) = {f_{0(\rm{X})}}{e^{ - \frac{{{Z_\rm{X}}F\varphi (x)}}{{RT}}}} $ | (5) |
因此,在t→∞时有:
| $ {N_\rm{X}}(t \to \infty ) = S{f_{0(\rm{X})}}{\int_0^l e ^{ - \frac{{{Z_\rm{X}}F\varphi (x)}}{{RT}}}}dx $ | (6) |
根据式(2)、式(3)和式(6),有:
| $ {k_{\rm{X}(1)}} = \frac{{{\pi ^2}{D_\rm{X}}S{f_{0(\rm{X})}}}}{{4{l^2}}}\int_0^l {{e^{ - \frac{{{Z_\rm{X}}F\varphi (x)}}{{RT}}}}} dx $ | (7) |
比较式(6)和式(7),有:
| $ {N_\rm{X}}(t \to \infty ) = \frac{{4{l^2}}}{{{\pi ^2}{D_\rm{X}}}}{k_{\rm{X}(1)}} $ | (8) |
式(8)清晰地表明,在黏土表面静电场驱动下X+/Cs+交换中X+在t→∞时的吸附量将依赖于一级吸附速率。吸附速率kX(1)越快,吸附量NX(t→∞)越大。实验中观测的阳离子吸附平衡态是亚稳态平衡,而不是真正的平衡,除非一级吸附速率达到最大值:
| $ \max {k_{\rm{X}(1)}} = \frac{{{\pi ^2}{D_\rm{X}}}}{{4{l^2}}}\left[ {\max {N_\rm{X}}(t \to \infty )} \right] = \frac{{{\pi ^2}{D_\rm{X}}}}{{4{l^2}}}\rm{CEC} $ | (9) |
式(9)中,CEC为阳离子交换量,此处CEC = 1 150 mmolc·kg−1。
另一方面,根据化学反应中的阿伦尼乌斯(Arrhenius)定律,X+/Cs+交换中X+的吸附速率常数可以表达为[27]:
| $ {k_{\rm{X}(1)}} = k{e^{ - \frac{{\Delta {w_\rm{X}}}}{{RT}}}} $ | (10) |
式(10)中,k为常数;∆wX(RT)为X+/Cs+交换体系中X+吸附的活化能。
显然,当∆w = 0时,有kX(1)= maxkX(1)。因此从式(10)可得k = maxkX(1)。进一步考虑式(9),有k = [π2DX/4l2]·CEC。因此式(10)变为:
| $ {k_{\rm{X}(1)}} = \frac{{{\pi ^2}{D_\rm{X}}}}{{4{l^2}}}{\rm{CEC}}{e^{ - \frac{{\Delta {w_\rm{X}}}}{{RT}}}} $ | (11) |
将式(11)代入式(8),有:
| $ {N_\rm{X}}(t \to \infty ) = {\rm{CEC}}{e^{ - \frac{{\Delta {w_\rm{X}}}}{{RT}}}} $ | (12) |
式(12)从理论上证实,当∆wX ≠ 0时有NX(t→∞) < CEC,意味着黏土中的离子吸附存在亚稳态平衡。
对于流动液相中的X+(即本体溶液中),有φ(x)→0,因此本体溶液中X+的势能为wX(液相)= ZXFφ(x)→0。另一方面,对于吸附相中的X+,有wX(吸附相)= ZXFφ(x) < 0。因此,吸附过程(从液相至吸附相)中X+势能的改变量为∆wX = ZXFφ(x) < 0。相应地,液相(本体溶液)中的Cs+有wCs(本体)= ZCsFφ(x)→0,在吸附相中有wCs(吸附相)= ZCsFφ(x) < 0。因此,解吸(从吸附相至液相)过程中Cs+的势能的改变量为∆wCs = −ZCsFφ(x) > 0。这意味着,X+/Cs+交换中X+吸附的活化能来源于Cs+解吸过程,因此有:
| $ \Delta {w_\rm{X}} = {Z_{Cs}}F\int_0^l {d\varphi (x) - {w_0}} $ | (13) |
以及
| $ {N_\rm{X}}(t \to \infty ) = {\rm{CEC}}{e^{ - \frac{{{Z_{Cs}}F\int_0^l {d\varphi (x) - {w_0}} }}{{RT}}}} $ | (14) |
上式中w0是未知的常数,当
根据经典胶体双电层理论,在任意给定浓度条件下的XNO3(此处X = K+、Na+和Li+),对于KNO3、NaNO3和LiNO3扩散层中的电位分布φ(x)相等,因此根据式(14),在给定的XNO3浓度条件下,X = K+、Na+和Li+的NX(t→∞)值相等。然而,根据表 2中所示,实验中得到的数据表明它们并不相等。这说明,即使是经典理论也预测了离子的亚稳平衡吸附态,但是它不能正确预测亚稳平衡态出现的离子特异性效应。
3.2 存在极化效应时离子亚稳平衡吸附的理论分析目前的研究表明,对于带电黏土颗粒,表面静电场引起的阳离子非经典极化将强烈影响离子交换平衡[28-30]和动力学[1,9-10]。当考虑阳离子非经典极化作用时,吸附阳离子平均力的总势能可以表达为[9,31-34]:
| $ w(x) \approx \gamma ZF\psi (x) $ | (15) |
式(15)中,ψ(x)为阳离子非经典极化存在时的电势,mV;γZ为利用库伦相互作用表征离子-黏土矿物间所有相互作用时离子的表观电荷数。
显然,当阳离子的非经典极化不存在时,式(15)将变为:
| $ w(x) \approx ZF\varphi (x) $ | (16) |
另一方面,X+/Cs+交换体系中的X+吸附过程,扩散层内电势ψ(x)可能近似视为依赖于吸附阳离子X+[35-36],因此根据式(15)和式(16)有:ψ(x)= φ(x)/γX。当阳离子非经典极化存在时,式(13)和式(14)中的ZCs应该换为γCsZCs,φ(x)应该换为φ(x)/γX。此处γCs和γX分别为Cs+和X+的表观电荷系数。
当考虑阳离子的非经典极化作用后,式(13)和式(14)变为:
| $ \Delta {w_\rm{X}} = \frac{{{\gamma _{Cs}}}}{{{\gamma _\rm{X}}}}F\int_0^l {d\varphi (x) - {w_0}} $ | (17) |
和
| $ {N_\rm{X}}(t \to \infty ) = {\rm{CEC}}{e^{ - \frac{{\Delta {w_\rm{X}}}}{{RT}}}} \approx {\rm{CEC}}{e^{ - \frac{{\frac{{{\gamma _{Cs}}}}{{{\gamma _\rm{X}}}}F\int_0^l {d\varphi (x) - {w_0}} }}{{RT}}}} $ | (18) |
在式(16)~式(18)中,φ(x)为经典电势,因此在相同浓度的不同X+离子(X+ = K+、Na+和Li+)体系中,φ(x)相等。式(18)意味着,X+的γX值越大,NX(t→∞)值越大。前期研究已经获得K+、Na+和Li+的γX值顺序为:1.942 > > 1.180 > 1.063[9],根据式(18),可推测出K+、Na+和Li+的NX(t→∞)值的顺序为:NK(t→∞) > NNa(t→∞) > NLi(t→∞)。表 2中NX(t→∞)的实验结果正好表现出相同的顺序,说明亚稳平衡态可通过考虑阳离子非经典极化作用的式(18)描述。
根据表 2中测得的NX(t→∞)值并结合式(18),可以计算得到活化能∆wX,结果如表 3所示。
|
|
表 3 Cs+-蒙脱石表面Li+、Na+、K+的吸附活化能 Table 3 The activation energy of Li+, Na+ and K+ adsorption on Cs+-montmorillonite surface |
对于X+ = i和j的两种体系,φi(x)=φj(x),由式(17)可得:
| $ \frac{{{\gamma _i}}}{{{\gamma _j}}} = \frac{{\Delta {w_j} + {w_0}}}{{\Delta {w_i} + {w_0}}} $ | (19) |
当考虑了表 3中测得的∆wX,并将w0=0.815 7RT[1]代入式(19),即可计算出其他浓度条件下的γK/γNa、γNa/γLi和γK/γLi值。计算结果列于表 4。
|
|
表 4 碱金属离子表观电荷系数比γK/γNa、γNa/γLi和γK/γLi。的理论计算值 Table 4 Theoretical calculation value of alkali metal ion apparent charge coefficient ratios γK/γNa, γNa/γLi and γK/γLi |
另一方面,根据黏土分散体系的阳离子交换选择性实验,得到γK/γNa、γNa/γLi和γK/γLi的值分别为1.646、1.110和1.699[24]。显然,本研究建立的离子交换吸附模型估算的γK/γNa、γNa/γLi和γK/γLi值与其他方法的测定值较为吻合(表 4)。上述结果证实,考虑阳离子非经典极化的离子交换吸附新模型能够正确评估阳离子吸附的活化能(式(17)),同时也能够正确描述黏土强电场中离子非经典极化影响下阳离子吸附的亚稳平衡态(式(18))。
4 结论碱金属离子(K+、Na+、Li+)在Cs+-蒙脱石饱和样表面的吸附动力学过程存在显著的亚稳平衡特征及特异性效应。交换离子的吸附活化能来源于蒙脱石表面吸附态Cs+解吸过程,该能量势垒是阻碍体系中交换离子达到理想吸附平衡的重要因素。虽然经典双电层理论能够解释体系活化能对离子亚稳平衡吸附的影响,但无法对亚稳平衡态的特异性效应进行合理化阐释。吸附态碱金属离子在带电表面产生强极化效应,极化能力较强的离子更易克服能量势垒,使其平衡吸附量更接近理想的离子吸附平衡,表现为相同离子浓度条件下,极化能力更强的离子其平衡吸附量更大。理论预测和实验结果均证实,表面静电场引发的离子强极化效应是导致离子亚稳平衡吸附及其特异性效应的根本原因。
| [1] |
Du W, Liu X M, Tian R, et al. Specific ion effects of incomplete ion-exchange by electric field-induced ion polarization[J]. RSC Advances, 2020, 10(26): 15190-15198. DOI:10.1039/D0RA01266A
(  0) 0) |
| [2] |
Pan X L, Liu X M, Li H, et al. Specificity of alkali metal ions absorbed on surface of montmorillonite-Cu2+ (In Chinese)[J]. Acta Pedologica Sinica, 2020, 57(2): 370-380. [潘小丽, 刘新敏, 李航, 等. 碱金属离子在蒙脱石-Cu2+表面吸附的离子特异性[J]. 土壤学报, 2020, 57(2): 370-380.]
(  0) 0) |
| [3] |
Wu Y B, Liu X M, Li R, et al. Hofmeister effect in eon adsorption kinetics on surface of yellow earth particles (In Chinese)[J]. Acta Pedologica Sinica, 2018, 55(6): 1450-1459. [吴英博, 刘新敏, 李睿, 等. 黄壤颗粒表面离子吸附动力学中的离子特异性效应[J]. 土壤学报, 2018, 55(6): 1450-1459.]
(  0) 0) |
| [4] |
Li R, Li H. Comparison study between Mg2+-K+ and Ca2+-K+ exchange kinetics under electric fields at the solid-liquid interface of soil (In Chinese)[J]. Acta Physico-Chimica Sinica, 2010, 26(3): 552-560. DOI:10.3866/PKU.WHXB20100310 [李睿, 李航. 土壤颗粒表面电场作用下固-液界面Mg2+-K+与Ca2+-K+交换动力学的比较研究[J]. 物理化学学报, 2010, 26(3): 552-560.]
(  0) 0) |
| [5] |
Park S M, Alessi D S, Baek K. Selective adsorption and irreversible fixation behavior of cesium onto 2: 1 layered clay mineral: A mini review[J]. Journal of Hazardous Materials, 2019, 369: 569-576. DOI:10.1016/j.jhazmat.2019.02.061
(  0) 0) |
| [6] |
Baek W, Ha S, Hong S, et al. Cation exchange of cesium and cation selectivity of natural zeolites: Chabazite, stilbite, and heulandite[J]. Microporous and Mesoporous Materials, 2018, 264: 159-166. DOI:10.1016/j.micromeso.2018.01.025
(  0) 0) |
| [7] |
Pan G. Metastable equilibrium adsorption theory: A challenge and development to classical thermodynamic adsorption theories (In Chinese)[J]. Acta Scientiae Circumstantiae, 2003, 23(2): 156-173. DOI:10.3321/j.issn:0253-2468.2003.02.003 [潘纲. 亚稳平衡态吸附(MEA)理论-传统吸附热力学理论面临的挑战与发展[J]. 环境科学学报, 2003, 23(2): 156-173.]
(  0) 0) |
| [8] |
Luo J M, Yu D Y, Hristovski K D, et al. Critical review of advances in engineering nanomaterial adsorbents for metal removal and recovery from water: Mechanism identification and engineering design[J]. Environmental Science & Technology, 2021, 55(8): 4287-4304.
(  0) 0) |
| [9] |
Du W, Li R, Liu X M, et al. Specific ion effects on ion exchange kinetics in charged clay[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2016, 509: 427-432. DOI:10.1016/j.colsurfa.2016.09.042
(  0) 0) |
| [10] |
Du W, Li R, Liu X M, et al. Estimating hofmeister energy in ion-clay mineral interactions from the gouy-chapman theory[J]. Applied Clay Science, 2017, 146: 122-130. DOI:10.1016/j.clay.2017.05.039
(  0) 0) |
| [11] |
Liu X M, Feng B, Tian R, et al. Electrical double layer interactions between soil colloidal particles: Polarization of water molecule and counterion[J]. Geoderma, 2020, 380: 114693. DOI:10.1016/j.geoderma.2020.114693
(  0) 0) |
| [12] |
Liu X M, Yang T, Li H, et al. Effects of interactions between soil particles and electrolytes on saturated hydraulic conductivity[J]. European Journal of Soil Science, 2020, 71(2): 190-203. DOI:10.1111/ejss.12855
(  0) 0) |
| [13] |
Li Q Y, Shi W Y, Yang Q Y. Polarization induced covalent bonding: A new force of heavy metal adsorption on charged particle surface[J]. Journal of Hazardous Materials, 2021, 412: 125168. DOI:10.1016/j.jhazmat.2021.125168
(  0) 0) |
| [14] |
Li Q Y, Yang S, Tang Y, et al. Asymmetric hybridization orbitals at the charged interface initiates new surface reactions: A quantum mechanics exploration[J]. The Journal of Physical Chemistry C, 2019, 123(41): 25278-25285. DOI:10.1021/acs.jpcc.9b07874
(  0) 0) |
| [15] |
Liu D, Du W, Liu X M, et al. To distinguish electrostatic, coordination bond, nonclassical polarization, and dispersion forces on cation–clay interactions[J]. The Journal of Physical Chemistry C, 2019, 123(4): 2157-2164. DOI:10.1021/acs.jpcc.8b08133
(  0) 0) |
| [16] |
Li H, Hou J, Liu X M, et al. Combined determination of specific surface area and surface charge properties of charged particles from a single experiment[J]. Soil Science Society of America Journal, 2011, 75(6): 2128-2135. DOI:10.2136/sssaj2010.0301
(  0) 0) |
| [17] |
Liu X M, Li H, Li R, et al. Combined determination of surface properties of nano-colloidal particles through ion selective electrodes with potentiometer[J]. The Analyst, 2013, 138(4): 1122-1129. DOI:10.1039/C2AN36069A
(  0) 0) |
| [18] |
Li H, Li R, Zhu H L, et al. Influence of electrostatic field from soil particle surfaces on ion adsorption–diffusion[J]. Soil Science Society of America Journal, 2010, 74(4): 1129-1138. DOI:10.2136/sssaj2009.0271
(  0) 0) |
| [19] |
Du W, Liu X M, Li R, et al. Theory to describe incomplete ion exchange in charged heterogeneous systems[J]. Journal of Soils and Sediments, 2019, 19(4): 1839-1849. DOI:10.1007/s11368-018-2204-z
(  0) 0) |
| [20] |
Li R, Li H, Xu C Y, et al. Analytical models for describing cation adsorption/desorption kinetics as considering the electrostatic field from surface charges of particles[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2011, 392(1): 55-66.
(  0) 0) |
| [21] |
Li R, Li H, Liu X M, et al. Combined measurement of surface properties of particles and equilibrium parameters of cation exchange from a single kinetic experiment[J]. RSC Advances, 2014, 4(47): 24671-24678. DOI:10.1039/c4ra02407a
(  0) 0) |
| [22] |
Li R, Li H, Zhu H L, et al. Kinetics of cation adsorption on charged soil mineral as strong electrostatic force presence or absence[J]. Journal of Soils and Sediments, 2011, 11(1): 53-61. DOI:10.1007/s11368-010-0283-6
(  0) 0) |
| [23] |
Rde Koning A, Comans R N J. Reversibility of radiocaesium sorption on illite[J]. Geochimica et Cosmochimica Acta, 2004, 68(13): 2815-2823. DOI:10.1016/j.gca.2003.12.025
(  0) 0) |
| [24] |
Sun J, Yang D J, Sun C H, et al. Potassium niobate nanolamina: A promising adsorbent for entrapment of radioactive cations from water[J]. Scientific Reports, 2014, 4: 7313.
(  0) 0) |
| [25] |
Colella C. Ion exchange equilibria in zeolite minerals[J]. Mineralium Deposita, 1996, 31(6): 554-562. DOI:10.1007/BF00196136
(  0) 0) |
| [26] |
Emmanuel T, Alfred D, Dimitri P, et al. Cation diffusion in the interlayer space of swelling clay minerals - A combined macroscopic and microscopic study[J]. Geochimica et Cosmochimica Acta, 2015, 149(1): 251-267.
(  0) 0) |
| [27] |
Jardine P M, Sparks D L. Potassium-calcium exchange in a multireactive soil system: I. Kinetics[J]. Soil Science Society of America Journal, 1984, 48(1): 39-45. DOI:10.2136/sssaj1984.03615995004800010007x
(  0) 0) |
| [28] |
Liu X M, Li H, Du W, et al. Hofmeister effects on cation exchange equilibrium: Quantification of ion exchange selectivity[J]. The Journal of Physical Chemistry C, 2013, 117(12): 6245-6251. DOI:10.1021/jp312682u
(  0) 0) |
| [29] |
Liu X M, Li H, Li R, et al. Strong non-classical induction forces in ion-surface interactions: General origin of hofmeister effects[J]. Scientific Reports, 2014, 4: 5047.
(  0) 0) |
| [30] |
Liu X M, Tian R, Du W, et al. A theory to determine the surface potentials of clay particles in electrolyte solutions[J]. Applied Clay Science, 2019, 169: 112-119. DOI:10.1016/j.clay.2018.12.022
(  0) 0) |
| [31] |
Huang X R, Li H, Li S, et al. Role of cationic polarization in humus‐increased soil aggregate stability[J]. European Journal of Soil Science, 2016, 67(3): 341-350. DOI:10.1111/ejss.12342
(  0) 0) |
| [32] |
Liu X M, Ding W Q, Tian R, et al. Position of shear plane at the clay–water interface: Strong polarization effects of counterions[J]. Soil Science Society of America Journal, 2017, 81(2): 268-276. DOI:10.2136/sssaj2016.08.0261
(  0) 0) |
| [33] |
Liu X M, Hu F N, Ding W Q, et al. A how-to approach for estimation of surface/stern potentials considering ionic size and polarization[J]. The Analyst, 2015, 140(21): 7217-7224. DOI:10.1039/C5AN01053E
(  0) 0) |
| [34] |
Xu C Y, Yu Z H, Li H. The coupling effects of electric field and clay mineralogy on clay aggregate stability[J]. Journal of Soils and Sediments, 2015, 15(5): 1159-1168. DOI:10.1007/s11368-015-1063-0
(  0) 0) |
| [35] |
Li H, Peng X H, Wu L S, et al. Surface potential dependence of the hamaker constant[J]. The Journal of Physical Chemistry C, 2009, 113(11): 4419-4425. DOI:10.1021/jp808372r
(  0) 0) |
| [36] |
Li H, Wu L S, Zhu H L, et al. Ion diffusion in the time-dependent potential of the dynamic electric double layer[J]. The Journal of Physical Chemistry C, 2009, 113(30): 13241-13248. DOI:10.1021/jp902302t
(  0) 0) |
 2023, Vol. 60
2023, Vol. 60


