2. 江西省水利科学院, 南昌 330029;
3. 萨斯喀彻温大学土壤科学系, 加拿大萨斯卡通市 S7N5A8
2. Jiangxi Academy of Water Science and Engineering, Nanchang 330029, China;
3. Department of Soil Science, University of Saskatchewan, Saskatoon S7N5A8, Canada
土壤热参数包括热导率、热扩散率和体积热容,影响着土壤的温度变化和能量传递。它和土壤含水率之间相互作用,共同控制着土壤中的水热交换和平衡过程[1-2]。目前热脉冲探针法(Heat pulse probe,HPP)是测定土壤热参数的标准方法,虽然被广泛应用于测量土壤水热参数,却受限于仅能在点尺度上进行测定[3-4]。由于土壤水热参数具有强烈的空间变异性[5],该方法在田间尺度应用时,测定结果不具代表性。因此,针对土壤水热参数测定点尺度与应用(田间)尺度不匹配的现状,亟需开发能够在田间尺度上同步测定的新技术和方法。
分布式温度传感技术(Distributed temperature sensing,DTS)的快速发展,为田间尺度上同步测定土壤水热参数提供了新方法。根据热源的不同,DTS测定土壤水热参数可分为被动加热光纤法(Passived heated fiber optic-DTS,PHFO-DTS)和主动加热光纤法(Active heated fiber optic- DTS,AHFO-DTS)两类。PHFO-DTS法不给光纤提供额外的热源,通过测定太阳辐射引起的温度变化推求土壤水热参数[6]。但在太阳辐射较弱时,PHFO-DTS的测定误差较大。AHFO-DTS基于探针无限线性热源理论,给光纤金属层短时间通电加热,通过解析加热和冷却过程温度的变化推求土壤水热参数。该方法能够在任意时间和任意土壤深度进行测量,相较于PHFO-DTS法,其应用更为广泛[7]。根据热脉冲探针类型的不同,AHFO-DTS可分为双探针热脉冲加热光纤法(DPHP-DTS)和单探针热脉冲加热光纤法(SPHP-DTS)。其中DPHP-DTS法能同时测量土壤热导率、热扩散率和比热容,并通过比热容推求土壤含水率[6]。但该方法的测量精度受光纤间距变化的影响很大[8],导致其应用受限。相比之下,SPHP-DTS法仅需埋设一条光纤,可避免上述缺陷。
SPHP-DTS法将光纤上某一段当成一根单探针,并将整条光纤看作由无数个单探针串联而成,因此可以实现土壤水热高时空分辨率的监测。该方法可以直接利用光纤被短时间加热后温度随时间的变化信息,如最大升温值(ΔTmax)[9]、累积升温值(ΔTcum)[10]与土壤含水率之间的函数关系,从而推求土壤含水率。此外,也可通过间接测定土壤热导率(λ)推求土壤含水率[11]。目前大部分研究[9,12-14]是利用最大升温值(ΔTmax)和累积升温值(ΔTcum)推求土壤含水率。然而,ΔTmax、ΔTcum与土壤含水率的关系为经验函数关系,其中的参数不具备物理意义。这些参数主要受光纤特性、土壤性质和加热策略等的影响[15],因此在不同的条件下测定需要重新校准,限制了SPHP-DTS法的发展。Ciocca等[11]已通过SPHP-DTS法测定λ。因此,在土壤含水率与λ关系已知的条件下,可通过λ估算土壤含水率。在土壤热导率预测方面,许多学者[16-17]建立了具有物理意义的热导率模型,为SPHP-DTS测定土壤含水率提供了模型基础。然而,目前缺乏对SPHP-DTS法测定土壤热导率误差的量化分析,其对土壤含水率测定精度的影响亟需深入研究。
本研究将单探针热脉冲加热光纤法(SPHP-DTS)和热脉冲探针法(HPP)测定土壤水热参数进行对比分析。以HPP法为参考,明确SPHP-DTS法的土壤热导率和含水率的测定精度,并探讨SPHP-DTS法测定土壤水热参数的误差来源,为SPHP-DTS法同步测定土壤水热参数提供理论证据。
1 材料与方法 1.1 试验设计本试验现场布设如图 1所示。本研究采用主动加热光纤法和热脉冲探针法测量不同质地土壤的水热参数。本试验所用土样取自杨凌渭河河岸带的砂土,杨凌农田褐土,长武和清涧苹果园黑垆土和黄绵土,后三种土壤质地为黏壤土。土样经风干后研磨过2 mm筛备用,土壤颗粒粒径分布体积分数如表 1所示。将4种不同的土壤通过多次分层压实的方法,分别装填在每个格子长宽高为0.8 m×0.3 m×0.3 m的不锈钢土槽中。首先对风干土进行测试,接着让土壤充分饱和,进行饱和土的测试。之后打开土槽底部的排水孔,监测从非饱和到干燥过程的土壤水热参数变化。为了加速土壤蒸发,在土槽上方悬挂红外灯泡加热土壤,加快土壤含水率变化速率,以缩短试验周期。为了避免红外灯泡的加热影响,每次进行热脉冲测试前,关闭红外灯,使土壤温度恢复至环境温度后开始测定。

|
图 1 干土(a)、非饱和土(b、c)水热参数测定试验 Fig. 1 Soil water content and thermal properties measurement under dry soil(a)and unsaturated soil(b, c) |
|
|
表 1 土壤粒径分布体积分数 Table 1 Soil particle size distribution volume fraction(%) |
本试验采用的光纤外径为4 mm,其不锈钢金属加热层电阻为1.88 Ω·m–1,光纤护套为聚氯乙烯材质。利用可调变压器给光纤两端通电加热,光纤的每次加热时间为10 min,加热功率为5 W·m–1。在光纤加热过程中,通过DTS(Silixa公司,Ultima,United Kingdom)记录光纤感应的温度变化,每隔5 s记录一次温度数据。同时,将土壤水分传感器TDR315(Acallima公司,USA)布置在光纤附近,该传感器通过烘干法校准,其水分测量精度约为0.03 m3·m–3。通过采用数据采集器(CR1000型号,Campbell Scientific公司,Logan,USA)每5 min采集1次土壤含水率数据。在光纤附近与TDR相对的位置布置自制的热脉冲探针。在加热光纤的同时,通过12V的蓄电池给探针提供一次持续15 s的脉冲加热(功率为45 W·m–1)。利用CR1000每秒采集一次温度数据。
1.2 分布式光纤温度传感技术测温原理在光纤中注入一定能量的脉冲泵浦光后,光子与光纤中的二氧化硅分子发生非弹性碰撞,产生2束背向拉曼散射光。其中,波长大于入射光的斯托克斯散射光不受温度影响,而波长小于入射光的反斯托克斯散射光有很强的温度依赖性。因此,可以根据斯托克斯与反斯托克斯的光强比计算温度,通过斯托克斯散射光的行走时间来定位,从而得到分布式温度测量值。两束背向散射光的光强比R(z)可表示为[18]:
| $ R(z) = Cexp - \left( { - \frac{\gamma }{T}} \right)exp(\Delta \alpha z) $ | (1) |
因此,只要根据光纤上某段或某几段已知参考温度标定出C、Δα和γ[19],即可得到光纤上任意一点z的温度值:
| $ T(Z) = \frac{\gamma }{{ln\left[ C \right] - ln\left[ {R(z)} \right] + \Delta \alpha z}} $ | (2) |
该温度值在光纤上的位置z,即为光行走路程的1/2:
| $ Z = \frac{{ct}}{{2n}} $ | (3) |
式中,c为光在真空中的速度(m·s–1);n为光纤包层的折射率;t为光向前与向后传播所需要的时间(s)。
1.3 土壤水热参数测定方法本研究通过主动加热光纤法(SPHP-DTS)和热脉冲探针法(HPP)测定土壤热导率和含水率。对于热导率的测定,HPP法利用峰值法求土壤体积热容和热扩散率[20],通过两者乘积计算热导率;SPHP-DTS法根据单探针原理,通过升温曲线到达稳定阶段的渐近线斜率计算热导率[11]。对于含水率的测定,SPHP-DTS利用最大升温值法(ΔTmax法)、累积升温值法(ΔTcum法)和热导率法(λ_FO法);HPP利用热导率法(λ_HP法)和热容法(C法)。
(1)ΔTmax法。由于加热阶段早期的温度数据受光纤热特性和接触热阻影响较大,Striegl和Loheide[9]将温度上升达到稳定阶段(升温值与时间的对数为线性关系)的平均值作为最大升温值ΔTmax。ΔTmax计算公式为:
| $ \Delta {T_{max}} = \frac{1}{N}\sum\nolimits_{{t_s}}^{{t_e}} {\Delta {T_i}} $ | (4) |
式中,ts为上述稳定阶段的起始时间,根据先验试验结果,本研究ts,取为390 s;te为停止加热的时间,本研究为600 s;ΔTi为第i个时刻的升温值(℃),由加热后该时刻的温度值减去初始温度值(加热前5 min温度的平均值)求得;N为稳定阶段内升温值的数量。
当加热条件一定时,ΔTmax随着土壤含水率增大而减小。利用测定的ΔTmax与水分的单调函数关系能推求土壤含水率。
(2)ΔTcum法。Sayde等[10]提出光纤加热后,土壤含水率越低则累积升温值ΔTcum越大,因此根据ΔTcum与土壤含水率的函数关系,ΔTcum可以用来推求含水率。ΔTcum计算公式为:
| $ \Delta {T_{cum}} = \int_0^{{t_e}} {\Delta {T_i}dt} $ | (5) |
(3)λ法。土壤含水率与热导率具有单调函数关系[21-26],本研究通过建立两者的经验函数关系推求含水率。
(4)C法。根据De Vries [27]模型,热容C的计算公式为:
| $ C = {\rho _b}{c_s} + {\rho _w}{c_w}\theta $ | (6) |
式中,ρwcw为水的容积热容量(M·J·m3·℃–1));θw为土壤体积含水率(m3·m–3);cs为土壤固体的比热(J·kg–1·℃–1),cs取自文献[28]中给定的值;ρb为土壤容重(kg·m–3),测试土壤容重约为1 530 kg·m–3。
由式(6)可以推求土壤含水率θ:
| $ \theta = \frac{{C - {\rho _b}{c_s}}}{{{\rho _w}{c_w}}} $ | (7) |
采用均方根误差(RMSE)评价加热光纤法和热脉冲探针法的土壤含水率测定精度,它是指TDR的水分观测值与加热光纤法和热脉冲探针法的测定值偏差的平方和观测次数n比值的平方根。RMSE能够很好地反映测量的精度,RMSE越小,表示测量精度越高。计算公式为:
| $ {\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^n {{{\left( {{X_{obs, i}} - {X_{pre, i}}} \right)}^2}} }}{n}} $ | (8) |
式中,Xobs,i为第i个TDR315观测值;Xpre,i为第i个光纤或探针的测定值。
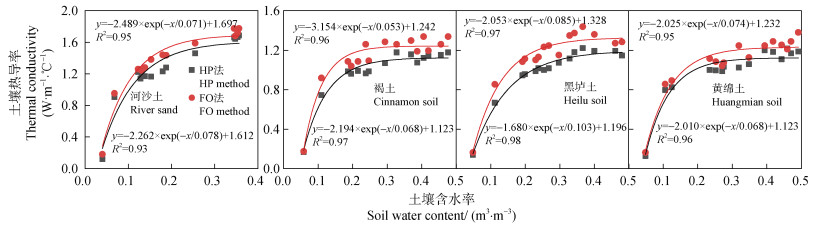
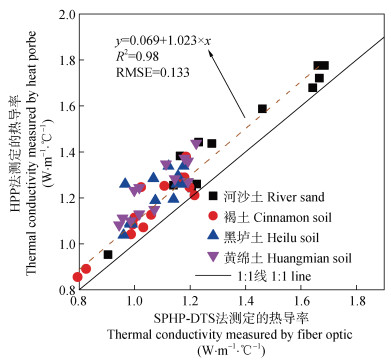
2 结果与讨论 2.1 SPHP-DTS法和HPP法测定土壤热导率的差异利用SPHP-DTS法和HPP法实测土壤在不同水分条件下的热导率,测定结果如图 2所示。可以看出SPHP-DTS法和HPP法测定的土壤热导率随含水率增加均呈指数上升的趋势,且具有较高的拟合度(R2>0.9)。随着含水率增加,土壤热导率的上升速率逐渐降低,表明热导率对含水率的敏感性逐渐降低。这是由于随着土壤含水率增加,颗粒之间形成“水桥”,大大增加了土壤热量传输的途径,因此土壤导热能力迅速增加,热导率随含水率呈指数增长[25]。当含水率增加到一定程度之后,增加的水分渐渐代替了土壤空气,因此,该阶段热导率随含水率增加呈缓慢增长趋势。当土壤饱和后,热导率达到稳定。此外,研究发现,在相同土壤含水率条件下,SPHP-DTS法测定的热导率显著高于HPP法(图 3),河沙土、褐土、黑垆土和黄绵土的SPHP-DTS法较HPP法分别平均高0.073、0.059、0.093和0.096 W·m–1·℃–1。这是因为,SPHP-DTS法加热光纤后温度升高值为5~15℃左右,远大于热脉冲探针法的最高值2℃,使得光纤周围的土壤温度偏高,可从两方面解释SPHP-DTS法的热导率高于HPP法:首先,土壤热导率随温度升高而增大;其次,光纤周围与土壤之间存在较大温度梯度,导致土壤中的水汽潜热传输增强[29]。
|
图 2 SPHP-DTS法和HPP法测定的土壤热导率与含水率的关系 Fig. 2 Relationship between soil thermal conductivity and water content by fiber optic and heat probe methods |
|
图 3 SPHP-DTS法和HPP法测定的热导率之间的关系 Fig. 3 Relationship between thermal conductivity measured by fiber optic and heat probe methods |
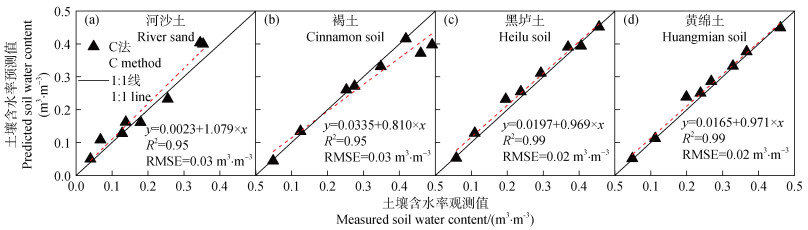
本研究采用基于HPP的热容法(C法)测定了4种类型土壤的含水率,相比于传统的时域反射法(TDR),河沙土、褐土、黑垆土和黄绵土的均方根误差(RMSE)分别为0.03、0.03、0.02、0.02 m3·m–3,测定精度与Tarara和Ham[30]的研究结果一致。在整个含水率范围内,土壤含水率观测值与预测值的散点均靠近1︰1线(图 4),因此C法测定土壤含水率具有很高的测量精度。
|
图 4 热容法的含水率测量精度 Fig. 4 Soil water content measurement accuracy of C method |
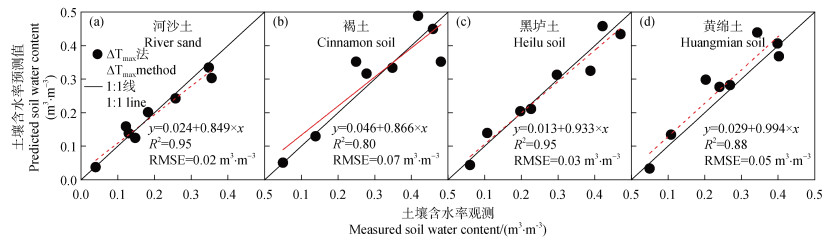
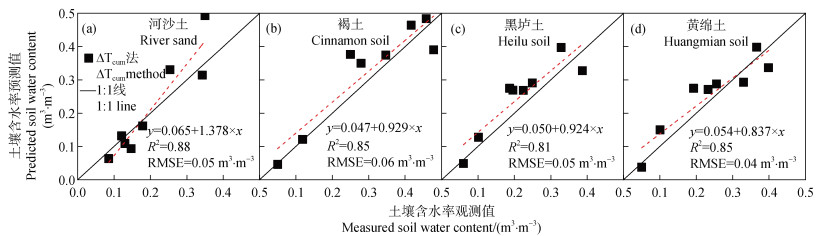
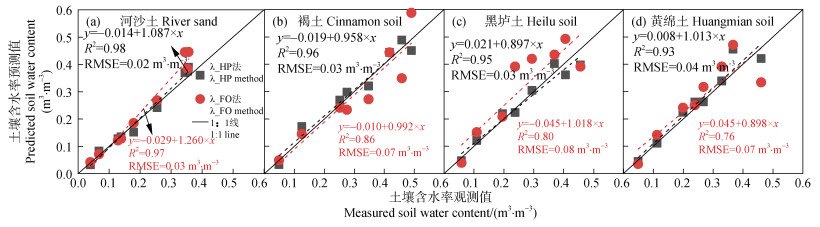
SPHP-DTS法和HPP法对不同质地土壤的水分测定精度具有一定的差异(图 5~图 7)。研究结果表明,对于河沙土,在整个水分范围内,两种方法均具有较高的测定精度,基于升温值法和热导率法的精度顺序为ΔTmax_FO=λ_HP>λ_FO>ΔTcum_FO。对于褐土、黑垆土和黄绵土,ΔTmax_FO法和ΔTcum_FO法的测量精度接近,且高于λ_FO法,这一结果与Li等[31]的研究结果一致。此外,研究发现在低含水率范围(小于0.2 m3·m–3),SPHP-DTS法表现出较好的测量精度。但在高含水率范围,观测值与预测值的散点偏离1︰1线,表明此时测定误差较大。这主要是因为随着土壤含水率的增加,热导率对水分的敏感性逐渐降低。同时,在高含水率条件下,光纤周围的水分容易在温度梯度的作用下发生迁移,从而导致水分测定误差增大。此外,研究发现,在河沙土、褐土、黑垆土和黄绵土的水分测定中,λ_FO法的测量精度RMSE分别较λ_HP法低0.01、0.04、0.05、0.03 m3·m–3(图 7)。该结果可能是由于SPHP-DTS法测定的热导率误差高于HHP法,进而影响土壤含水率测定。
|
图 5 ΔTmax_FO法的含水率测量精度 Fig. 5 Soil water content measurement accuracy of ΔTmax_FO method |
|
图 6 ΔTcum_FO法的含水率测量精度 Fig. 6 Soil water content measurement accuracy of ΔTcum_FO method |
|
图 7 λ_FO法和λ_HP法的含水率测量精度对比 Fig. 7 The comparison of water content measurement accuracy between λ_HP and λ_FO method |
因此,为提高SPHP-DTS在λ_FO法下的土壤含水率测量精度,有必要以HHP法为基准对SPHP-DTS法测定的热导率进行校正,从而提高HHP法的土壤含水率测定精度。从本研究可以看出,HHP法对不同质地类型土壤的水分测定具有很高精度(RMSE小于0.05 m3·m–3)。目前许多学者[16-17]建立了具有物理意义的热导率模型λ(θ),为SPHP-DTS法水分测定提供了可靠的模型基础。因此,在热导率准确测定的前提,SPHP-DTS法测定土壤含水率具有广阔的应用前景。
2.3 SPHP-DTS法测定水热参数的误差本研究测定结果表明,以HPP法为标准,SPHP-DTS测量土壤热导率的精度RMSE为0.13 W·m–1·℃–1。因此,在利用SPHP-DTS测定土壤热导率时,有必要通过HPP法的测定结果进行校准,以免SPHP-DTS法高估土壤热导率。两种方法的线性回归结果为
| $\lambda_{\text {SPHP-DTS }}=0.069+1.023 \times \lambda_{\text {HPP }}, \quad R^2=0.98$ | (9) |
利用上式,可以将SPHP-DTS法热导率校正为HPP法的热导率值。
陆森等[29]研究表明多针加热针在测定时的温度升高值为20℃左右,远大于标准单针法的最高值2℃,使得多针加热针周围的土壤温度偏高,导致探针周围土壤热导率的温度效应,使多针热脉冲法的热导率测定值高于单针法。相同的是,本研究加热光纤的温度升高值在5~15℃之间,在温度效应的作用下,导致SPHP-DTS法测定的土壤热导率高于HPP法。Liu等[32]研究表明,由于探针体积和接触热阻的存在,导致HPP法测定的土壤热导率被低估。本研究光纤直径为探针的4倍,光纤与土壤之间涉及多个界面的接触热阻(纤芯-空气层-金属层-护套-土壤),因此光纤体积和接触热阻远大于探针。但SPHP-DTS法测定的热导率显著高于HPP法,可以说明SPHP-DTS法的温度效应对测定热导率的影响大于接触热阻。
综合前人及本研究的结果,SPHP-DTS法测定土壤水热参数的误差主要来源于以下4个方面:(1)SPHP-DTS法的温升远大于HPP法,引起土壤热导率的温度效应。在测定过程中,光纤周围土壤温度显著升高,不仅增加了土壤热导率,而且促进了水汽潜热传输,进而导致SPHP-DTS法的热导率高估。(2)光纤的结构和材料与热探针相比存在巨大差异,光纤与土壤间的接触热阻远大于探针,从而对测量精度造成显著影响[33]。因此,在田间布设光纤时,可采用自制埋线装置,以减小土壤扰动,从而降低光纤护套与土壤之间的接触热阻。(3)光纤的温度测量精度以及对温度的敏感性远低于探针,导致加热和冷却过程中出现升温值的波动,进而引入噪音干扰影响测定结果。(4)SPHP-DTS法要求输入较HPP法更多的热量且延长加热时间,以提高信噪比,这可能使光纤周围的水分在温度梯度的作用下产生迁移[34],进而影响土壤水热参数测定。因此,在应用SPHP-DTS法测定土壤热导率时,需要以HPP法校准,控制好加热功率,升温不宜过高。此外,为了减小接触热阻的影响,可选择结构简单、直径小且导热性好的光纤,以使其接近无限线性热源,从而提高测量精度。
为了进一步深入研究,可从光纤加热策略和自身的特性出发,考虑光纤升温、结构和材料对SPHP-DTS法测量的影响,从而提高其测定土壤水热参数的准确性和普适性。在目前SPHP-DTS法受测温精度和温度敏感性制约的情况下,随着光纤温度解调仪的精度、敏感性以及时空分辨率不断提高,未来有望通过分布式光纤温度传感技术,实现田间从厘米至千米范围的土壤水热参数原位同步测定。
3 结论本研究通过开展加热光纤法和热脉冲探针法测定土壤水热参数的对比试验,分析了它们在测定土壤热导率和含水率的精度,并探讨了加热光纤法测定土壤水热参数的误差来源。研究可得出以下结论:(1)以热脉冲探针法为参考,加热光纤法测定热导率的精度RMSE为0.13 W·m–1·℃–1。在利用加热光纤法测量热导率时,有必要以热脉冲探针法为标准进行校准。(2)通过热导率法测定土壤含水率时,加热光纤法的测定精度明显低于热脉冲探针法。在整个土壤范围,加热光纤法测定的热导率显著高于热脉冲探针法。主要原因在于光纤法在测定时土壤升温较大,导致了光纤周围土壤热导率的温度效应。(3)加热光纤法测定土壤水热参数的其他误差来源包括光纤与土壤之间多个界面的接触热阻(纤芯-空气层-金属层-护套-土壤)、光纤的温度敏感性、噪音干扰以及温度梯度驱动下的水分迁移。(4)未来研究应充分考虑加热策略、光纤结构和材料的影响,以提高光纤法测定土壤水热参数的准确性和普适性。
| [1] |
Zhang N, Wang Z Y. Review of soil thermal conductivity and predictive models[J]. International Journal of Thermal Sciences, 2017, 117: 172-183. DOI:10.1016/j.ijthermalsci.2017.03.013
(  0) 0) |
| [2] |
Demyanyuk O S, Patyka V P, Sherstoboeva О V, et al. Formation of the structure of microbiocenoses of soils of agroecosystems depending on trophic and hydrothermal factors[J]. Biosystems Diversity, 2018, 26(2): 103-110. DOI:10.15421/011816
(  0) 0) |
| [3] |
Kojima Y, Heitman J L, Noborio K, et al. Sensitivity analysis of temperature changes for determining thermal properties of partially frozen soil with a dual probe heat pulse sensor[J]. Cold Regions Science and Technology, 2018, 151: 188-195. DOI:10.1016/j.coldregions.2018.03.022
(  0) 0) |
| [4] |
Ren T, Noborio K, Horton R. Measuring soil water content, electrical conductivity, and thermal properties with a thermo-time domain reflectometry probe[J]. Soil Science Society of America Journal, 1999, 63(3): 450-457. DOI:10.2136/sssaj1999.03615995006300030005x
(  0) 0) |
| [5] |
Brocca L, Melone F, Moramarco T, et al. Spatial- temporal variability of soil moisture and its estimation across scales[J]. Water Resources Research, 2010, 46(2): W02516.
(  0) 0) |
| [6] |
Benítez-Buelga J, Sayde C, Rodríguez-Sinobas L, et al. Heated fiber optic distributed temperature sensing: A dual-probe heat-pulse approach[J]. Vadose Zone Journal, 2014, 13(11): 1-10.
(  0) 0) |
| [7] |
He H L, Dyck M F, Horton R, et al. Distributed temperature sensing for soil physical measurements and its similarity to heat pulse method[J]. Advances in Agronomy, 2018, 148: 173-230.
(  0) 0) |
| [8] |
Liu G, Si B C. Errors analysis of heat pulse probe methods: Experiments and simulations[J]. Soil Science Society of America Journal, 2010, 74(3): 797-803. DOI:10.2136/sssaj2009.0116
(  0) 0) |
| [9] |
Striegl A M, Loheide S P II. Heated distributed temperature sensing for field scale soil moisture monitoring[J]. Groundwater, 2012, 50(3): 340-347. DOI:10.1111/j.1745-6584.2012.00928.x
(  0) 0) |
| [10] |
Sayde C, Gregory C, Gil-Rodriguez M, et al. Feasibility of soil moisture monitoring with heated fiber optics[J]. Water Resources Research, 2010, 46(6): W06201.
(  0) 0) |
| [11] |
Ciocca F, Lunati I, van de Giesen N, et al. Heated optical fiber for distributed soil-moisture measurements: A lysimeter experiment[J]. Vadose Zone Journal, 2012, 11(4): vzj2011.0199. DOI:10.2136/vzj2011.0199
(  0) 0) |
| [12] |
Vidana Gamage D N, Biswas A, Strachan I B. Actively heated fiber optics method to monitor three-dimensional wetting patterns under drip irrigation[J]. Agricultural Water Management, 2018, 210: 243-251. DOI:10.1016/j.agwat.2018.08.019
(  0) 0) |
| [13] |
Liu X F, Zhu H H, Wang J C, et al. Experimental study on actively heated fiber Bragg grating method for sensing seepage in unsaturated soils (In Chinese)[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(8): 1443-1452. [刘喜凤, 朱鸿鹄, 王家琛, 等. 非饱和土水分迁移感测的主动加热光纤光栅法试验研究[J]. 岩土工程学报, 2022, 44(8): 1443-1452.]
(  0) 0) |
| [14] |
Hu Y, Li M, Ren H Y, et al. Measurement of soil water content using distributed temperature sensor with heated fiber optics (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(10): 42-49. [胡优, 李敏, 任姮烨, 等. 基于加热光纤分布式温度传感器的土壤含水率测定方法[J]. 农业工程学报, 2019, 35(10): 42-49.]
(  0) 0) |
| [15] |
Dong J Z, Agliata R, Steele-Dunne S, et al. The impacts of heating strategy on soil moisture estimation using actively heated fiber optics[J]. Sensors, 2017, 17(9): 2102. DOI:10.3390/s17092102
(  0) 0) |
| [16] |
Lu Y L, Lu S, Horton R, et al. An empirical model for estimating soil thermal conductivity from texture, water content, and bulk density[J]. Soil Science Society of America Journal, 2014, 78(6): 1859-1868. DOI:10.2136/sssaj2014.05.0218
(  0) 0) |
| [17] |
Zhao Y, Si B C, Zhang Z H, et al. A new thermal conductivity model for sandy and peat soils[J]. Agricultural and Forest Meteorology, 2019, 274: 95-105. DOI:10.1016/j.agrformet.2019.04.004
(  0) 0) |
| [18] |
Rogers A. Distributed optical-fibre sensing[J]. Measurement Science and Technology, 1999, 10(8): R75-R99. DOI:10.1088/0957-0233/10/8/201
(  0) 0) |
| [19] |
Hausner M B, Suárez F, Glander K E, et al. Calibrating single-ended fiber-optic Raman spectra distributed temperature sensing data[J]. Sensors: Basel, Switzerland, 2011, 11(11): 10859-10879. DOI:10.3390/s111110859
(  0) 0) |
| [20] |
Ren T S, Shao M A, Ju Z Q, et al. Measurement of soil physical properties with thermo-time domain reflectometryI. Theory (In Chinese)[J]. Acta Pedologica Sinica, 2004, 41(2): 225-229. [任图生, 邵明安, 巨兆强, 等. 利用热脉冲-时域反射技术测定土壤水热动态和物理参数Ⅰ. 原理[J]. 土壤学报, 2004, 41(2): 225-229.]
(  0) 0) |
| [21] |
Kersten M. Thermal properties of soils [D]. Minneapolis: University of Minnesota, 1949: 23—24.
(  0) 0) |
| [22] |
Johansen O. Thermal conductivity of soils [D]. Trondheim: Norwegian Institute of Technology, 1977: 189—193.
(  0) 0) |
| [23] |
Campbell G S. Soil physics with basic - Transport models for soil-plant systems . Amsterdam: Elsevier, 1985.
(  0) 0) |
| [24] |
Côté J, Konrad J M. A generalized thermal conductivity model for soils and construction materials[J]. Canadian Geotechnical Journal, 2005, 42(2): 443-458.
(  0) 0) |
| [25] |
Lu S, Ren T S, Gong Y S, et al. An improved model for predicting soil thermal conductivity from water content at room temperature[J]. Soil Science Society of America Journal, 2007, 71(1): 8-14.
(  0) 0) |
| [26] |
He H L, Flerchinger G N, Kojima Y, et al. Evaluation of 14 frozen soil thermal conductivity models with observations and SHAW model simulations[J]. Geoderma, 2021, 403: 115207.
(  0) 0) |
| [27] |
De Vries D. Thermal properties of soils . Amsterdam: North-Holland Publishing Co., 1963: 210-235.
(  0) 0) |
| [28] |
Ren T, Ochsner T E, Horton R, et al. Heat-pulse method for soil water content measurement: Influence of the specific heat of the soil solids[J]. Soil Science Society of America Journal, 2003, 67(6): 1631-1634.
(  0) 0) |
| [29] |
Lu S, Ren T S, Yang Y, et al. Error analysis of multi- needle heat pulse probe for soil thermal conductivity measurement (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 26(6): 20-25. [陆森, 任图生, 杨泱, 等. 多针热脉冲技术测定土壤热导率误差分析[J]. 农业工程学报, 2010, 26(6): 20-25.]
(  0) 0) |
| [30] |
Tarara J M, Ham J M. Measuring soil water content in the laboratory and field with dual-probe heat-capacity sensors[J]. Agronomy Journal, 1997, 89(4): 535-542.
(  0) 0) |
| [31] |
Li M, Si B C, Hu W, et al. Single‐probe heat pulse method for soil water content determination: Comparison of methods[J]. Vadose Zone Journal, 2016, 15(7): 1-13.
(  0) 0) |
| [32] |
Liu G, Si B C, Jiang A X, et al. Probe body and thermal contact conductivity affect error of heat pulse method based on infinite line source approximation[J]. Soil Science Society of America Journal, 2012, 76(2): 370-374.
(  0) 0) |
| [33] |
Qiao Z Y, Diao W Y, Liu G. Improved thermal probe method for in situ measurement of thermal conductivity of solid materials (In Chinese)[J]. Journal of Engineering Thermophysics, 2018, 39(5): 1085-1091. [乔照钰, 刁万英, 刘刚. 原位测量固体材料热导率的改进热探针方法[J]. 工程热物理学报, 2018, 39(5): 1085-1091.]
(  0) 0) |
| [34] |
Zhu F Y, Zhou Y S, Zhu S P. Experimental study on moisture migration in soil during coupled heat storage and release processes[J]. Energy and Buildings, 2021, 242: 110986.
(  0) 0) |
 2024, Vol. 61
2024, Vol. 61


