美国土壤学会前主席Gardner^[1]曾指出，土壤学还没有形成一套完整的系统化知识体系从而实现对土壤过程的预测，土壤学知识过于碎片化。Gardner^[2]甚至希望土壤学能够从“第一性原理”出发来实现对土壤任意过程的描述。Gardner所指的“第一性原理”本质上就是量子力学原理。澳大利亚学者Churchman^[3]指出，土壤的独特性在于“土壤胶体-土壤团聚体-土体构型”三个方面，而且正是这三方面的独特性导致现代自然科学所依赖的“还原论”方法在土壤学研究中不再适用。现代自然科学所基于的“还原论”方法是指：先对研究对象的“整体”进行分解，在分解和分析的基础上通过“综合”而最终还原于“整体”。因此，Churchman^[3]认为，土壤科学应突破土壤物理、土壤化学与土壤生物学等各分支学科的边界，从“土壤胶体-土壤团聚体-土体构型”三个层次去整体地进行研究。其实现代自然科学中的“宏观热力学”正是研究系统整体发展/演化行为的科学，其方法论很值得土壤学借鉴。由此引出本文关注的两个问题：（1）量子力学能否“直接”作为基础土壤学知识体系的基石并包含在土壤学的知识内容之中？（2）如何突破土壤学各分支学科边界去整体地研究土壤？对第一个问题的回答就是寻找基础土壤学新的理论基础并由此构建新的知识内容，对第二个问题的回答就是寻找土壤学知识体系重建的方法基础。

本文严格论证了土壤学之所以是独立于其他自然学科学的独立学科，那就是土壤具有其他物质体系所不具有的独特量子效应。所以基础土壤学知识体系必须在这独特量子效应的科学描述上重建。这也是土壤学与一般物质科学的知识体系进行区分的关键点。

1 基础土壤学知识体系重建的必要性

本文所指的基础土壤学核心知识是指描述土壤“形成、组成、性质、过程、功能及其相互关系”的那部分知识。土壤学界一些人认为基础土壤学知识“大厦”的主体已基本建成，未来的工作似乎主要是对已有理论的应用和对这座“理论大厦”做些“修修补补”的工作，基础土壤学不大可能有更大的未来；甚至认为，土壤学只是一门“应用型”学科，土壤学基础研究的深化就是没有意义的“钻牛角尖”。美国土壤学会前主席Gardner对土壤学界的这些错误认识也表达出了类似的担忧。在美国土壤学会出版的Opportunity in Basic Soil Science Research一书的序言中^[1]，Gardner曾指出：“一些人（错误地）认为与土壤有关的知识值得了解的已完全了解，目前要做的仅仅是对这些知识加以适当的应用而已。即使学识渊博的科学家也常常错误地认为，其他学科发现的自然科学规律和理论，不需要任何想象和创新就可以直接运用于土壤学的研究当中。在他们看来，土壤学不过是应用生物学、应用化学或者应用物理学的一种表现形式”。Gardner甚至提醒我们：“所有那些认为我们对土壤完全了解的人们，会发现自己已经置身于一百多年前相信科学知识是有极限的自然科学家的行列”。

整体而言，土壤学研究的基本现状是：从微观到宏观的各尺度研究相互割裂，土壤物理、土壤化学和土壤生物学等分支学科彼此分裂，理论研究和应用研究彼此脱离。按Gardner说法，目前的土壤科学太碎片化^[2]。近些年来，全球粮食问题、生态与环境问题促使人们对土壤的关注集中在解决这些现实问题方面。虽然这是土壤学发展的重大机遇，但令人遗憾的是，它也在一定程度上导致了人们对该学科基础科学问题的忽视。如果土壤学不能建立一套各尺度彼此关联、各学科分支彼此融合的知识体系，理论研究与应用研究彼此脱离的问题就无法解决，土壤学这门学科就无法应对未来需求所面临的巨大挑战。Churchman^[3]认为，土壤科学应突破土壤物理、土壤化学与土壤生物学等各分支学科的边界，从“土壤胶体-土壤团聚体-土体构型”三个层次去整体地进行研究。Gardner^[2]希望土壤学能够直接从“第一性原理”（即量子力学原理）出发实现对土壤任意过程的描述。这些观点均反映了土壤及土壤学知识体系的独特性。本文正是基于土壤这一独特物质，提出了重新构建其独特知识体系的可能性。本文的基本判断是：如果对于“原子”的量子力学描述构建了物理、化学和生物学等现代自然科学的基础，那么土壤“电场-原子”相互作用的量子力学描述可以成为构建基础土壤学核心知识体系的基础。现有的基础土壤学是直接应用物理学、化学和生物学等基础科学的知识，而在这些学科中物质的原子轨道描述均未考虑外电场对原子轨道的影响。所以土壤学必须基于“电场-原子”相互作用而建立自己的原子轨道理论。

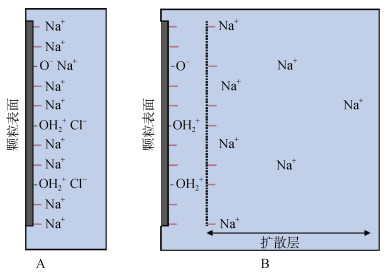
“电场”是土壤十分重要的基本属性，土壤中“电场-原子”相互作用无处不在。于天仁院士^[4]曾经指出，土壤电荷是土壤一切过程发生的根本原因，是土壤肥力的基础。虽然土壤中既有正电荷也有负电荷，但地球上所有土壤均带有数量十分庞大的净负电荷。当然，这些负电荷将吸附等量正电荷（阳离子）而使土壤在宏观上处于电中性。然而，由于这些吸附态阳离子因热运动而在土壤颗粒（包括有机和无机颗粒）表面附近空间形成扩散状分布：Boltzmann分布，导致土粒表面负电荷产生的电场不能被吸附态阳离子充分屏蔽，进而使土粒表面及其附近空间形成很强的负电场^[5-12]。比如，一个负电荷量为20 cmol·kg^–1（近似等于土壤阳离子交换量），比表面积为50 m²·g^–1的土壤，按Gauss公式进行计算可以发现该土壤的平均表面电场在土壤水介质中可达5×10⁸ V·m^–1，而在空气介质中则高达4×10¹⁰ V·m^–1。即使在距离土壤颗粒表面100 nm处，该电场仍然可以达到~10⁴ V·m^–1的强度（取决于土壤含水量和土壤电解质构成）^[13]。下图给出了土壤电荷被吸附态反离子平衡（或中和）的两种可能方式（以Na⁺为阳离子、Cl^–为阴离子为例）。

上图是假定土粒表面有9个负电荷两个正电荷的情形。从图 1A可以看出，当土壤含水量→0或本体溶液电解质浓度→∞时，Debye特征长度或扩散层厚度→0，此时颗粒表面9个表面负电荷被9个Na⁺中和，2个表面正电荷被2个Cl^–中和。从图 1B可以看出，当土壤含水量不为0或本体溶液电解质浓度为一有限值时，Debye特征长度不为0，土粒周围将存在一个厚度近似等于Debye特征长度的负电场空间；此时Cl^–难以越过该负电场区域而到达表面正电荷点，而且即使达到了表面也难以稳定地吸附于负电场的表面上（除非发生了专性吸附），所以只有7个Na⁺以扩散状分布的方式去中和表面的7个净负电荷。此时，表面上那2个正电荷产生的静电效应也因其与表面9个负电荷之间的电势叠加而被抵消。显然，虽然这两种方式均可使土壤达到电中性，但通常情况下土壤将采用图 1B那样的方式去平衡表面电荷。图 1B中7个Na⁺的Boltzmann分布就是土粒表面7个净负电荷在土壤中形成负电场的原因。

土壤另一个独特属性是土粒表面原子组成。虽然土壤固相物质组成非常复杂，包括各种矿物质、有机质和微生物，但通常情况下只有处于土粒表面的那些原子才直接参与土壤各种过程的发生，因此我们只需关注土粒表面原子的组成状况。其实，土壤物质的表面原子组成非常地简单。对于土壤中的2︰1型层状硅酸盐矿物而言，表面原子几乎全是O原子；对于1︰1型黏土矿物而言，表面原子50%是O原子50%是OH；对于土壤中的各种氧化物颗粒而言，表面原子也以O和OH为主；对于有机大分子而言，表面活性原子仍然主要是O以及各种OH和NH₂。很有意思的是，土粒表面上的这些O、OH和NH₂与溶液中的H⁺和OH^–发生相互作用后可使土壤颗粒表面带正电或负电，因而也是土壤电荷或电场的重要来源。

由此表明，无论土壤组成多么复杂，土壤电场和土粒独特而简单的表面原子组成正是该体系最基本、最重要的特性。我们以此为线索，或许可以构建一套独具特色的基础土壤学知识体系，即：基于对土壤“电场-原子”相互作用的科学描述，及其与各尺度土壤物理、化学、生物学过程的定量关联研究，或许可以打破土壤学各分支学科间的知识壁垒，最终建立一套新的基础土壤学核心知识体系。

2 土壤学核心知识体系构建的方法基础

长期以来，土壤学研究在方法论上存在两种截然不同的观点：一种观点认为土壤学必须“综合/整体”地开展研究，另一种观点认为土壤学必须进入“原子/分子尺度”开展研究。此处的讨论将发现，正确的方法论是能够将这二者间的矛盾统一起来。

借助于“宏观热力学”的方法论启示，为实现从整体上去研究土壤，在方法论上必须首先找到恰当的“宏观物理量”，使得这种物理量是土壤某方面的局部或微观性质在宏观尺度上的“整体综合”的表达，从而实现“微观与宏观”“局部与整体”的统一。在宏观热力学中，人们熟知的“温度”这一物理量就属于系统的宏观物理量，它是系统中原子/分子复杂微观运动状态在宏观尺度上的综合或叠加，这在数学上表达为求和。如气体的温度为^[14]：

$T = \frac{2}{{3k}}\left[ {\frac{1}{2}M\left( {\frac{1}{n}\sum {{n_i}v_i^2} } \right)} \right]$

(1)

式中，v_j为分子千变万化的运动速度；M为某物质的分子质量；k为Boltzmann常数；n_i为以v_i速率运动的分子数，n₁ + n₂ +…..+n_i = n；$\frac{1}{n}\sum {{n_i}v_i^2}$为分子运动速率平方的平均值。

虽然获得体系中单个气体分子在任意时刻的运动速率是困难的，但式（1）表明，人们只需要利用“一根温度计”就可以获得体系中所有分子的“整体”动能或速率。与此同时，进一步借助于温度T与“自由能G”这一宏观物理量相联系^[15]就能对系统的整体发展/演化行为做出判断。

${\left( {\frac{{\partial G}}{{\partial n}}} \right)_{T, P}} = \frac{R}{n}T$

(2)

式中，n为物质的量，R为气体常数，P为压强，T为绝对温度。

由于系统的“宏观物理量”就是那些对微观或局部进行整体求和的物理量，所以土壤中那些基于长程相互作用的物理量就属于这种“宏观物理量”。土壤中能满足这种基于长程作用而实现对微观或局部求和的宏观物理量首推电势和电场两个物理量。由于电场是长程作用，所以土壤中任何一点的电势或电场可看成土壤中所有电荷（包括全部正负电荷）产生的电势或电场在该处的叠加。简而言之，土壤颗粒上的电荷是微观的、局部的，但电场则是宏观的、综合的。

类似于式（1）的求和关系，土壤电势可表达为如下求和：

${\psi _p} = \frac{1}{{4\pi \varepsilon }}\sum {\frac{{{q_i}}}{{{r_i}}}}$

(3)

式中，ψ_p为空间p点的电势；q_i为电荷；r_i为i电荷至p点的距离；ε为介质介电常数。

相应地，电场强度可表达为：

${\stackrel{\rightharpoonup }{E}}_{p}=\frac{1}{4\pi \epsilon }{\displaystyle \sum \frac{{q}_{i}}{{r}_{i}}}3\stackrel{\rightharpoonup }{{r}_{{}_{i}}}$

(4)

式中，${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} _p}$为空间p点的电场强度。

虽然式（3）和式（4）表达出了空间电势和电场的这种“整体求和”的特征，但人们无法直接利用这两个公式去求土壤中的电势和电场分布，因为从微观上去确定土壤中每个电荷点的位置是不可能的。但土壤中的电势分布、电场分布、电荷密度分布，以及土粒间静电排斥力/能等等，均可通过求解如下的Poisson-Boltzmann方程而得到^[16]：

$\nabla^2 \mathtt{ψ}(\mathrm{r})=\frac{4 \pi F}{\varepsilon} \sum\limits_i c_{i 0} z_i e^{-\frac{z_i F \mathtt{ψ}(\mathrm{r})}{R T}}$

(5)

式中，${c_{i0}}$为价数为z_i的i离子在本体溶液中的浓度；F为Faraday常数。

在式（5）的求解中，土粒表面电势是土粒表面所有电荷和扩散层中所有吸附态反离子电荷所产生的电势在表面上的叠加。

土壤中除了“电场”这一长程相互作用外，还存在另外四种长程相互作用而成为土壤的“宏观物理量”：

（1）土壤中的渗透力。溶质渗透力可以阻止土壤颗粒的相互吸引，因而产生一种“长程排斥”作用^[17]。由于它是对土壤中所有电解质求和，因而土壤颗粒间的渗透力（p_o）可以表达为：

${p_o}\left( x \right) = RT\sum\limits_i {{c_{i0}}} \left( x \right)$

(6)

（2）土壤中的长程范德华力。土壤中的长程范德华力是对土壤固体颗粒中的所有分子/原子的范德华力求和，因而土粒间的长程范德华力位能可表达为^[18]：

$\begin{aligned} w_{v D W}(d) & =-\sum \frac{\beta_i}{r_i^6} \\ & =-2 \pi N_0 \iint_0^{\infty} \frac{\beta_i \rho_i}{M_i} \frac{y d y d z}{\left[(d+z)^2+y^2\right]^3} d y d z \\ & =-\frac{A}{12 \pi} \frac{1}{d^2} \end{aligned}$

(7)

式中，w_vDW为土粒间的总范德华力位能（即土壤中各组分分子引力位能的加和）；ρ_i为i物质密度，M_i为i物质的摩尔质量；d为土粒间距离；N₀为Avogadro常数；β_i为与物质分子的偶极矩、极化率和独立特征振动频率有关的常数；A为与土壤物质组成有关的常数，也称Hamaker常数。

范德华力本为短程力（位能与距离r的6次方成反比），但对所有原子/分子“求和”后就在土壤中变成了长程力（位能与距离d平方成反比）。

（3）土壤中的长程亲水作用力。土壤颗粒与水分子间的亲水作用是一种长程作用，因为土壤颗粒表面与极性水分子间存在静电相互作用和共价相互作用^[19-20]，这两种作用会通过水分子传递到距土粒表面很远的位置。但在土粒间相互作用中，长程亲水力有时表现为引力，有时又表现为斥力。当土壤发生从“干到湿”的变化过程时，土粒表面对大量水分子的吸附迫使土粒间距离增加，从而使土壤团聚体或整个土体发生膨胀而表现为“排斥”；当土壤发生从“湿到干”的变化过程时，随着土粒间水分子的渐渐失去，土粒间剩余的那些水分子依靠其形成的长距离引力作用渐渐地将土粒拉到一起，从而使土壤团聚体收缩或整个土体收缩而在宏观上表现为“吸引”。

（4）土粒间的长程疏水作用力。土粒表面的疏水作用主要来自于有机质疏水部分对水分子的排斥作用，也表现为长程作用。由于疏水作用导致水分子无法进入带有疏水区域的土粒表面附近空间，所以这些颗粒间的水合排斥力将不再存在。另一方面，疏水作用导致土壤颗粒表面附近的“反离子扩散层”无法形成，从而导致土粒间的长程静电力也由此消失。因此，土壤中的疏水作用也表现为长程作用，而且疏水作用在土粒相互作用中将表现为“引力”效应，因而提高土壤团聚体的稳定性和土壤的抗蚀性。

此处要特别强调的是，一般情况下只需要这五个“宏观物理量”就足以去描述土壤矿物、有机、微生物等土壤颗粒间的相互作用、土壤颗粒的堆积方式与稳定性，进而描述土壤结构孔隙状况，以及结构孔隙变化动力学等重要的介观与宏观行为。不仅如此，这些“宏观物理量”还定量地联系着原子、分子甚至亚原子尺度上的土壤行为（这些将在后面部分做详细讨论）。所以这五个“宏观物理量”对于开展土壤多尺度和多过程的定量关联研究具有关键性意义。

3 土壤学核心知识体系构建的理论基础：土壤电场中的原子/离子轨道

众所周知，人们基于原子结构的量子力学描述构建了现代自然科学（包括土壤学）的基础。然而，已有原子结构的量子力学描述没有考虑“外电场”对原子轨道的影响。从前面的讨论可知，土壤是一个充满电场的体系，该电场对于其中的任何一个原子而言均属于外电场。显然一个不考虑外电场的原子结构理论不能直接应用于土壤。目前的大量实验证据显示，土壤中的原子/离子轨道的确发生了很大改变^[21-27]。

在经典原子结构理论中（不考虑外电场作用）的Hamilton算符为^[28]：

$\bar H = \frac{\hbar }{{2m}}{\nabla ^2} + \frac{{Z{e^2}}}{r} + w\left( r \right)$

(8)

式中，$\bar H$为Hamilton算符；$\hbar = \frac{h}{{2\pi }}$，h为Planck常数；Z为核电荷数；e为电子电量；m为电子质量；w为核外电子中对某个电子而言其他电子对该电子的电势能的贡献（如果考虑类氢原子情况^[28]，则w=0）。

相应的描述经典原子结构的Schrodinger方程为^[28]：

$\bar{H} \mathtt{ψ}(\mathbf{r})=E \mathtt{ψ}(\mathbf{r})$

(9)

式中，$\mathtt{ψ}(\mathbf{r})$为波函数即原子轨道；E为波函数或轨道$\mathtt{ψ}(\mathbf{r})$对应的能量。

Schrodinger方程表明，Hamilton算符决定了波函数或原子轨道$\mathtt{ψ}(\mathbf{r})$及其能量E。显然，在经典的原子结构理论中，原子轨道量子力学描述中的那个位能算符只考虑了原子的核电荷对某电子的位能贡献$\frac{{Z{e^2}}}{r}$和核外所有电子对这个电子位能的贡献w。但是，土壤存在电场，而土壤中的电场对于一个原子中的电子而言属于附加的外电场。所以，土壤中的原子轨道必定不同于人们熟知的经典原子轨道。其实，著名土壤化学家Sposito早就认为，土壤中原子轨道的这种改变必定普遍性地发生^[16，29]。

3.1 土壤原子轨道改变的量子力学基础

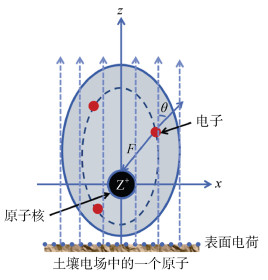
我们关注的土壤电场分布于土粒表面和土壤溶液所构成的空间部分，而且由于这个电场随离开表面距离的增加而下降，所以对于土粒表面和溶液中的原子而言，这个电场是非对称的，见图 2。

根据图 2，在土壤电场中的Hamilton算符为^[30]：

$\bar H = \frac{\hbar }{{2m}}{\nabla ^2} + - \frac{{Z{e^2}}}{r} + w\left( r \right) + e{\text{ξ }}r\cos \theta$

(10)

式中，$e{\text{ξ rcos}}\theta$为土壤电场$\zeta$施加给核外电子的电势能。

将式（10）与式（8）比较可发现，土壤中原子的Hamilton算符不同于经典原子轨道的Hamilton算符。根据Schrodinger方程式（9），Hamilton算符决定了原子轨道或波函数$\mathtt{ψ}(\mathbf{r})$及其能量E，所以土壤电场ζ改变了土壤中原子轨道的量子力学基础。

前面提到，地球上所有土壤所带电荷为净负电荷，因此外电场的场强ζ为负。据此，从土壤电场对核外电子Hamilton量的贡献可以看出一个重要特性：在图（2）中z > 0的远离外电场场源的上半空间，因r∙cosθ > 0导致该电场对核外电子的排斥作用使得该空间的电子能量提高（外电场使电子远离原子核）；而该图中在z < 0的靠近外电场场源的下半空间，因r∙cosθ < 0导致该电场对核外电子的排斥作用使该空间电子的能量降低（外电场将电子压向了原子核方向）。这一属性对于我们选择土壤原子的电子轨道叠加方式具有重要的指导意义。

3.2 土壤中的原子轨道及其能量

因土壤原子轨道的Schrodinger方程包含$r\cos \theta$乘积项，所以不能像经典理论那样通过变量分离来求解。但由于土壤电场强度一般≤ 10¹⁰ V/m，而原子内的电场强度一般 > 10¹² V/m。前者较后者至少低2个数量级，因此可采用微扰理论进行求解。由于原子/离子的最外层轨道才容易受到土壤电场的“扰动”，所以通常情况下我们只需考虑土壤中原子的最外层轨道。下面仅给出土壤中外层轨道为1s、2s2p和3s3p的原子/离子轨道。

（1）土壤中外层为1s的原子/离子轨道与能量

外层轨道为1s的原子包括Li⁺离子和H原子等。将式（10）带入式（9）求解得到外层为1s的原子轨道与能量：

$\varphi_{\text {soil }}=\mathtt{ψ}_{1 \mathrm{~s}}, {\text{ }}{E_{{\text{soil1}}}} = {E_{10}}$

(11)

式中，$\mathtt{ψ}_{1 \mathrm{~s}}$为经典轨道，${E_{10}}$为相应的轨道能量；${\varphi _{{\text{soil}}}}$为土壤原子轨道，${E_{{\text{soil1}}}}$为相应的轨道能量。后面涉及的轨道和能量符号的含义与此类似，所以不再讨论其定义。有关经典轨道（波函数）和能量的数学表达式可以参见有关《结构化学》书籍^[28]。

式（11）表明，外层轨道为1s的原子/离子在土壤中的轨道和能量与经典原子轨道和能量相同，即在微扰近似下土壤表面电场没有改变这些原子的轨道。

（2）土壤中外层为2s2p的离子/原子轨道与能量

外层为2s2p的原子/离子轨道包括Na⁺，Mg²⁺，Al³⁺，-O，-N，···（应注意的是，土壤中的原子均是以离子或分子态形式存在的）。由于土壤颗粒表面绝大多数原子是O原子，所以2s2p外层轨道的这种改变在土壤中具有特别重要的意义。将式（10）带入式（9）求解得到土壤中具有2s2p外层轨道的原子/离子轨道与能量^[31]：

$\begin{cases}\varphi_{\text {soil(1) }}=\frac{1}{\sqrt{2}}\left[\mathtt{ψ}_{2 s}+\mathtt{ψ}_{2 p z}(-)\right], & E_{\text {soil2 }}^1=E_{20}+3 e \xi \frac{a_0}{(1-a) Z} \\ \varphi_{\text {soil(2) }}=\frac{1}{\sqrt{2}}\left[\mathtt{ψ}_{2 s}+\mathtt{ψ}_{2 p z}(+)\right], & E_{\text {soil2 }}^2=E_{20}-3 e \xi \frac{a_0}{(1-a) Z} \\ \varphi_{\text {soil(3) }}=\mathtt{ψ}_{2 p x}, & E_{\text {soil2 }}^3=E_{20} \\ \varphi_{\text {soil}(4)} =\mathtt{ψ}_{2 p y}, & E_{\text {soil2 }}^4=E_{20}\end{cases}$

(12)

式中，a₀为Bohr半径；a = S/Z，其中S为屏蔽常数，Z为核电荷数；E_soil2为土壤电场中轨道能量，E₂₀为相应的经典轨道能量。

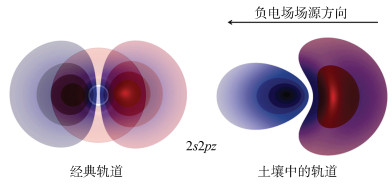
表明，土壤电场改变了具有2s2p外层轨道的原子在z方向上的原子轨道，而x，y两个方向的原子轨道没有改变。$3e{\text{ξ }}\frac{{{a_0}}}{{\left( {1 - a} \right)Z}}$为轨道能量的改变值。利用式（12）可以直接绘出土壤中2s2p_z轨道图，见图 3^[31]。图 3表明，土壤中的2s2p_z轨道的确发生了很大改变。

（3）土壤中外层为3s3p的原子/离子轨道与能量

土壤中外层为3s3p的原子/离子轨道包括K⁺，Ca²⁺，-S，-P，···。将式（10）带入式（9）求解得到土壤中具有3s3p外层轨道的原子/离子的轨道与能量为^[31]：

$\begin{cases}\varphi_{\mathrm{soil}(1)}=\frac{1}{\sqrt{2}}\left[\mathtt{ψ}_{3 s}+\mathtt{ψ}_{3 p z(-)}\right], & E_{\mathrm{soil3}}^1=E_{30}+\frac{18}{\sqrt{6}} e \xi \frac{a_0}{(1-a) Z} \\ \varphi_{\mathrm{soil}(2)}=\frac{1}{\sqrt{2}}\left[\mathtt{ψ}_{3 s}+\mathtt{ψ}_{3 p z(+)}\right], & E_{\mathrm{soil3}}^2=E_{30}-\frac{18}{\sqrt{6}} e \xi \frac{a_0}{(1-a) Z} \\ \varphi_{\text {soil}(3)}=\mathtt{ψ}_{3 p x}, & E_{\mathrm{soil3}}^3=E_{30} \\ \varphi_{\mathrm{soil}(4)}=\mathtt{ψ}_{3 p y}, & E_{\mathrm{soil3}}^4=E_{30}\end{cases}$

(13)

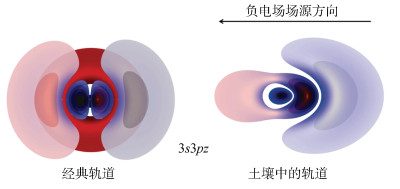
同样地，土壤电场改变了具有3s3p外层轨道的原子/离子在z方向上的原子轨道。根据轨道能量的改变值可以发现，3s3p外层轨道的改变程度比2s2p外层轨道的改变程度大。利用式（13）可以直接绘出土壤中3s3p_z外层轨道图，见图 4^[30]。

采用同样的方法也可以获得土壤中其他原子的外层轨道，如含d轨道的重金属和过度金属离子在土壤电场中的外层轨道^[31]。

4 土壤中独特的原子轨道是构建土壤学新知识体系的基础

土壤中独特的原子轨道必将通过其对原子/分子结构与性质的影响深刻地作用于各尺度土壤物理、化学和生物学过程的发生，进而影响土壤性质和功能的产生。可以说，“原子轨道变了，一切都变了”。所以，基于土壤中独特的原子轨道，有望重新构建基础土壤学核心知识体系。下面的讨论将表明，土壤中原子轨道改变将带给我们对不同尺度土壤过程及其相互关联的全新认识。

4.1 原子尺度土壤表面原子活性新认识

土壤中的2︰1型黏土矿物表面几乎全部是O原子，1︰1型黏土矿物表面50%是O原子50%是OH基团，各种氧化物（含水合物）和大分子有机质表面也主要为O原子和OH基团，所以土壤颗粒表面原子活性实际上就是表面O原子（包括OH中的O）的活性。前面的量子力学分析结果表明，在土粒表面负电场中外层轨道为2s2p的表面O原子轨道和轨道能量均发生了改变。从图 3可以看出，在靠近土粒表面一端的轨道上（蓝色）电子云密度增加，电子云被压缩到离核更近的区域。根据式（12），此时轨道能量降低了$3e{\text{ξ }}\frac{{{a_0}}}{{\left( {1 - a} \right)Z}}$。然而，在远离土粒表面（或远离负电场场源）一端（红色），电子云密度降低，电子云被外电场排斥而远离原子核分布。根据式（12），此时轨道能量提高了$3e{\text{ξ }}\frac{{{a_0}}}{{\left( {1 - a} \right)Z}}$。显然，只有远离土粒表面一端的轨道才能够与表面附近溶液中的离子/原子/分子轨道形成成键轨道。表明，在土粒表面电场中表面O原子被活化了。由于土粒表面氧原子用于成键的电子是其孤对电子，所以表面O原子被活化的本质是其孤对电子的活性得到了提高，导致表面O原子与离子/原子/分子形成配位键的可能性提高了。从结构化学可知，黏土矿物表面O孤对电子活性本身是很低的，属于Lewis软碱^[16]。但此处的量子力学分析表明，在表面电场中的这些O原子不再是该Lewis软碱了。其实，Sposito^[29]曾经指出，伊利石类矿物与K⁺形成内圈配位的根本原因正是黏土矿物表面O原子的孤对电子活性被表面电荷产生的电场提高所致。

4.2 分子尺度土壤表面化学反应新认识

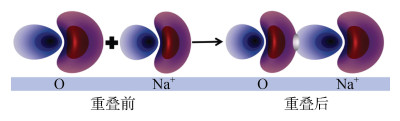
一方面，当土粒表面O原子的外层2s2p轨道被土壤电场激活后使这些O原子具有更高的化学反应活性；另一方面，那些与表面O发生反应的离子/原子/分子的外层轨道也会在这个电场中发生相应的改变而被激活，从而诱发这些离子/原子/分子在土粒表面发生新的化学反应。由于这种新的化学反应是参与反应的离子/原子外层轨道被土壤电场激活后而发生的，所以可将土壤中这种新化学反应的成键方式称为极化诱导共价^[30]。与此同时，由于土壤表面原子/离子发生极化的极化率远大于经典极化率，所以可称其为非经典极化^[30]。此处我们仅以外层轨道为2s2p的Na⁺和外层轨道为3s3p的K⁺分别与土粒表面O原子间的反应为例来说明。图 5为O-Na⁺轨道重叠图。

从图 5的O-Na⁺轨道重叠图可以看出，O和Na⁺轨道重叠部分的轨道符号相反（红色为+，蓝色为-），因此轨道重叠后重叠区域的电子云密度下降。表明O-Na⁺之间不能发生极化诱导共价^[30]。其次，从式（12）可以看出，轨道重叠部分O的2s2p轨道能量从E₂₀提高了$3e{\text{ξ }}\frac{{{a_0}}}{{\left( {1 - a} \right)Z}}$，而成键方向上Na⁺的2s2p轨道能量从E₂₀下降了$3e{\text{ξ }}\frac{{{a_0}}}{{\left( {1 - a} \right)Z}}$，所以二者能量也无法匹配。这进一步表明土粒表面O-Na⁺之间不能发生极化诱导共价^[31]。

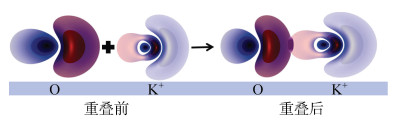
图 6为O-K⁺轨道重叠图。从图 6的O-K⁺轨道重叠图可以看出，O和K⁺重叠部分的轨道符号相同（均为+），因此轨道重叠后重叠区域的电子云密度提高。表明O-K⁺之间可发生极化诱导共价^[30]。其次，从式（12）和式（13）可以看出，轨道重叠部分O的2s2p轨道能量从E₂₀提高了$3e{\text{ξ }}\frac{{{a_0}}}{{\left( {1 - a} \right)Z}}$，而K⁺的3s3p轨道能量从E₃₀下降了$\frac{{18}}{{\sqrt 6 }}e{\text{ξ }}\frac{{{a_{\text{0}}}}}{{\left( {{\text{1}} - a} \right)Z}}$，二者能量有可能匹配。所以，土粒表面O-K⁺之间可发生极化诱导共价^[30]。

表面除发生极化诱导共价外，由于电子云或原子/离子轨道强烈的非对称畸变可使此处的吸附态Na⁺和K⁺形成电场诱导偶极子（这是基于非经典极化的大偶极子）。从式（12）和式（13）可以看出，Na⁺和K⁺在土壤电场中的诱导偶极子的偶极矩分别为$3e{\text{ξ }}\frac{{{a_0}}}{{\left( {1 - a} \right)Z}} = 0.4839{a_0}e$和$\frac{{18}}{{\sqrt 6 }}e\frac{{{a_{\text{0}}}}}{{\left( {{\text{1}} - a} \right)Z}} = {a_0}e$，表明K⁺偶极子的偶极矩是Na⁺的2.067倍^[30]。

综合上述分析可以看出以下几点：

（1）在土粒表面Na⁺除了+1个电荷的静电吸附力外，还获得了因离子非经典极化而产生的偶极矩为0.4839a₀e的大偶极子吸附力；即Na⁺在土粒表面存在两种作用力。

（2）在土粒表面K⁺除了获得+1个电荷的静电吸附能外，还获得了因离子极化而产生的偶极矩为a₀e（两倍于Na⁺）的大偶极子吸附力，以及极化诱导共价吸附力；即K⁺在土粒表面存在三种作用力。

（3）由于在土壤电场中Li⁺轨道没发生改变，所以在土粒表面Li⁺只存在+1个电荷的静电吸附力；即Li⁺在土粒表面只存在一种作用力。

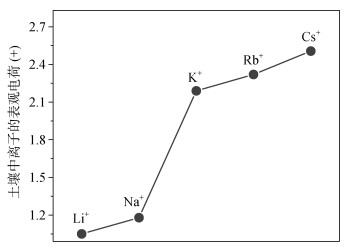
这些理论分析结果已经从离子吸附选择系数、土壤胶体凝聚等方面得到了实验验证^[12，31-36]。对于带+1个电荷的碱金属离子而言，如果将各种非静电吸附能在表观效应上看成离子价数改变后的静电吸附能时，实验得到的Li⁺、Na⁺、K⁺（以及Rb⁺和Cs⁺）的表观电荷由图 7所示^[30，36]。

图 7表明：（1）随Li⁺、Na⁺、K⁺（以及Rb⁺和Cs⁺）离子半径（电子层数）增加，离子电子云变形性增加导致离子非经典极化程度增加，进而使得离子的表观电荷增加；（2）离子的表观电荷大于+1说明离子间的差异不是来自于离子水合半径差异，因为水合效应将导致离子的表观电荷小于+1；（3）与其他的两相邻离子比较，K⁺较Na⁺的表观电荷呈现出剧烈增加，这正是因为土壤中K⁺产生了Na⁺所没有的新界面反应：极化诱导共价。

前面仅以碱金属离子为例来说明土壤电场改变了原子轨道，从而使土壤表面化学反应呈现出新的特征。而对于土壤中的其他离子/原子甚至分子均可发生类似的界面化学反应。比如，当表面O原子的孤对电子被电场激活后，H⁺与表面O原子发生极化诱导共价而成为可能，这意味着土壤中2︰1型黏土矿物并非真正的恒电荷胶体，或者说土壤中并没有真正的恒电荷胶体。当然，由于这种极化诱导共价是电场依赖的，而随着O-H⁺极化诱导共价的发生，土壤负电场强度将随之下降，而当下降到一定程度后极化诱导共价将不复存在，所以2：1型表面只能发生有限量的O-H⁺极化诱导共价。又比如，NH₄⁺中N-H配位键结合的那个H也可与黏土矿物表面O发生极化诱导共价（极化诱导氢键），而且这种共价在20世纪70年代就已经被实验证实^[16]。显然，由于NH₄⁺可在黏土矿物表面发生这种非静电吸附，所以NH₄⁺似乎不能作为测定土壤中阳离子交换量的指示离子。再比如水分子被电场极化后，水分子中的H与土粒表面O原子发生极化诱导共价而改变了带电颗粒表面水分子的结构^[19-20]。

这些新的界面反应不仅影响到土粒表面状况，甚至会影响土粒自身，即影响“土壤基质”过程的发生。比如层状铝硅酸盐矿物中硅氧四面体表面被活化了的O与H⁺的“极化诱导共价”作用可能导致四面体中Si-O键键能的改变，进而影响铝硅酸盐矿物晶体的稳定性，这可能是土壤矿物深度风化、Al³⁺释放和土壤酸化的真正原因。

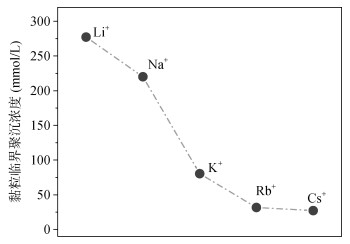
4.3 介观尺度土粒相互作用新认识

介观尺度即纳微米尺度，土壤中矿物质、有机质和微生物等“土粒”大多位于此尺度。然而，介观尺度上土粒相互作用由五个“宏观物理量”决定：静电力、长程范德华力、渗透力、亲水力和疏水力。此处我们仅讨论土粒凝聚。对于土粒凝聚而言，当液体中电解质浓度低于0.1 mol/L时，只需考虑土粒间的静电力和长程范德华力两个力。对于给定的土壤固相组成，其长程范德华力可以认为是不变的，而静电力则强烈地受到离子界面反应的影响。根据图 7，同为一价的碱金属离子，但因它们界面反应方式和强度的不同将导致其屏蔽土壤电场的能力遵循如下顺序：Cs⁺ > Rb⁺ > K⁺ > > Na⁺ > Li⁺，进而导致土粒间静电力遵循Li⁺ > Na⁺ > > K⁺ > Rb⁺ > Cs⁺。因此可以推测，土粒凝聚的临界聚沉浓度（critical coagulation concentration，CCC）将表现出与图 7正好相反的趋势，即Li⁺ > Na⁺ > > K⁺ > Rb⁺ > Cs⁺。图 8是蒙脱石颗粒凝聚的激光散射实验结果^[34-35]。从图 8可以看出，实验结果与基于离子界面反应的理论推测一致，表明原子/分子尺度上的界面反应决定了介观尺度上的土粒相互作用。

4.4 宏观尺度土壤过程发生的内因动力新认识

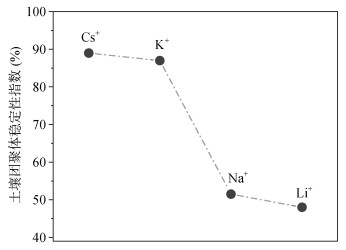
首先看土壤团聚体稳定性这一宏观土壤过程发生的内因动力。如果离子界面反应后导致土壤电场变弱，土粒间的静电排斥力就降低，土壤团聚体的稳定性必定增高。根据图 7，同样为一价的碱金属离子，因它们界面反应方式和强度的不同将导致其屏蔽土壤电场的能力遵循如下顺序：Cs⁺ > K⁺ > > Na⁺ > Li⁺，进而导致土粒间静电排斥力遵循Li⁺ > Na⁺ > > K⁺ > Cs⁺。因此可以推测，土壤团聚体的稳定性将表现出Li⁺ < Na⁺ < < K⁺ < Cs⁺的序列。图 9是根据Li⁺、Na⁺、K⁺、Cs⁺作用下紫色土团聚体破碎释放出的 < 2μm土粒百分数^[27]换算成稳定性指数所得到的团聚体稳定性图。从图 8可以看出，实验结果与基于离子界面反应的理论推测相符。表明，原子/分子尺度上的界面反应通过影响介观尺度上的土粒相互作用，最终影响了宏观尺度上的土壤团聚体稳定性。

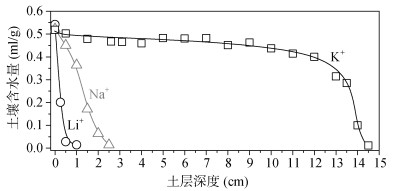
再来看土壤水分运移这一土壤宏观过程发生的内因动力。图 10是三种不同碱金属离子存在时水分入渗140 min时同一紫色土中的含水量分布图^[25]。从该图可以看出，在相同的离子浓度下土壤水的运移速率明显地表现出K⁺ > > Na⁺ > Li⁺。显然，土壤水运动的实验结果也与前面的“亚原子-原子/分子-介观”三个不同尺度的土壤过程相符。从土壤离子/原子轨道改变，到原子/分子尺度上的界面反应，到介观尺度上土壤颗粒相互作用，再到宏观尺度土壤团聚体稳定性和土壤水运动的理论分析和实验结果表明，土壤水运动的深层次内因动力首先是土壤电场改变了土壤中的离子/原子轨道，然后再从分子尺度上改变了离子/原子的界面反应，进而改变了介观尺度上土粒间的静电排斥力，从而影响了宏观尺度上土壤团聚体的稳定，并最终影响了土壤水传输。因为水分传输过程中土壤团聚体的稳定性决定了土壤孔隙状况变化的动力学，进而反过来又影响了宏观尺度上土壤水分传输。由于土壤孔隙是土壤系列物理、化学和生物学过程发生的重要场所^[37]，所以可以认为“电场”是土壤物理、化学和生物学过程发生的关键内因动力。

综上所述，原子/分子尺度上的离子界面反应方式与强度的巨大差异（图 7）必然引起介观尺度土粒相互作用的巨大差异（图 8），进而引起宏观尺度土壤团聚体稳定性程度（图 9）和土壤水传输速率（图 10）的巨大差异，而离子界面反应方式和强度差异则来自于亚原子尺度上这些离子外层轨道发生改变的性质和强度差异。因此，此处清晰地呈现出“亚原子-原子/分子-介观-宏观”不同尺度土壤过程间的关联。

需要再次强调的是，此处仅仅以碱金属离子“界面过程”的量子效应为例而展开的讨论，其涉及的理论和方法同样适用于其他“界面过程”、“基质过程”与“孔隙过程”。

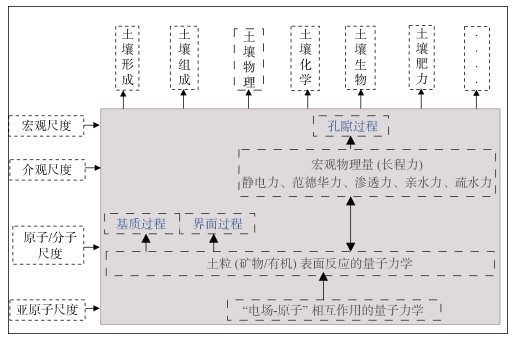
5 新知识体系的逻辑结构

综合上述分析，基础土壤学核心知识的逻辑框架可以构建出来，见图 10。在新的知识体系中，“电场-原子”相互作用是知识体系的基石，它发生在亚原子尺度；基质过程是表面反应引发的土壤固相物质的化学和生物化学转化过程，它发生在原子与分子尺度；界面过程是基于表面反应的物理、化学和生物学过程，它也发生在原子或分子尺度；孔隙过程是由分布于整个土壤的五种长程力（或宏观物理量）所决定的宏观物理、化学和生物学过程，而这些长程力是直接通过作用于介观尺度上土壤“矿物-有机-微生物”相互作用来影响土壤孔隙过程的发生。土壤生物学过程主要发生在土壤颗粒表面和土壤孔隙之中，而新的知识体系基于“电场-原子”相互作用对土壤界面过程和孔隙过程将进行系统性描述，从而将土壤物理学、土壤化学和土壤生物学联系在一起。显而易见，图 11表达的基础土壤学核心知识体系不仅打破了土壤学各分支学科之间的边界，而且还明确了土壤学在各尺度间的逻辑关系。

6 结论

经典土壤学核心知识体系是建立在经典原子结构理论基础之上的。但土壤电场引发了土壤原子/离子轨道的重大改变，所以应该在这新的基石上重新构建土壤学核心知识体系。由于土壤组成和过程的复杂性导致土壤系统呈现的每一种效应均是整体综合的，所以在构建新知识体系的方法论上，必须首先找到那些基于长程相互作用的“宏观物理量”。本文提出了建立基础土壤学核心知识体系所需的五个独立的宏观物理量：静电力、范德华力、渗透力、亲水力和疏水力。本文以三种一价金属离子为例分析了亚原子尺度上土壤“电场-原子”相互作用如何通过影响原子/离子轨道，进而影响原子/分子尺度上的界面反应，并借助于五个长程力影响介观尺度上的土壤颗粒相互作用，从而最终影响宏观尺度上的土壤团聚体稳定和土壤水分运移。结果表明，基于“电场-原子”相互作用的量子力学并借助于五个宏观物理量有望实现对“土壤基质过程”、“土壤界面过程”和“土壤孔隙过程”的描述。而另一方面，可以认为土壤中一切物理、化学和生物学过程可以归纳为“土壤基质过程”、“土壤界面过程”和“土壤孔隙过程”三个方面，所以基于本文提出的理论和方法，人们有望构建新的基础土壤学核心知识体系。