掌握准确的土壤类型空间分布,能为土地规划利用、农业生产生活等提供更可靠的参考依据。数字土壤制图(Digital soil mapping)通过土壤属性与地理环境的协同变化关系,利用多种数学方法和空间分析方法进行区域内土壤属性的推理预测[1],并凭借其高效性、低成本、高精度等特点逐渐得到广泛应用[2]。由其推理过程可知,选取合适的环境因子、使用恰当的推理方法是数字土壤制图研究过程中的重点内容。
环境因子选取的有效性直接决定着数字土壤制图的精确度[3]。有较多的研究在进行环境因子选取时,直接将母质作为一种预测因子用于推理制图[4-5]。但母质作为土壤发育形成的物质基础和植物矿物元素的最初来源,会直接影响成土的过程和速度[6-7],当制图点的样本量较少时直接进行环境因子筛选很有可能会降低母质在所有因子中的重要性。黄魏等[8]按照母质类型使用5个地形因子对研究区环境因子进行规则挖掘以实现推理制图,然而该研究更侧重于利用少量地形因子进行传统土壤图的更新,同时也并未深入探究母质类型对环境因子选择的具体影响。
机器学习常用于各领域的回归和分类任务[9-10],在数字土壤制图中,应用较多的机器学习方法如决策树,随机森林,支持向量机,人工神经网络等[11-13],支持向量机算法与KNN算法在土壤类型分类预测的理论基础上具有一定的相似性[14]。这些方法均通过环境因子与土壤类型的关系根据算法自身特点进行推理预测,在很大程度上忽略了环境因子本身存在的关联关系。本文选用了随机森林方法(Random Forest,RF)、基于C5.0决策树的土壤景观推理模型方法(Soil-land Inference Model,SoLIM)、K邻近算法(K-Nearest Neighbor,KNN)作为推理预测方法,并在此基础上使用FP-Growth(Frequent Pattern Growth,FP-Growth)算法挖掘环境因子关联关系,通过本研究设计的结合流程将环境因子关联关系分别与三种制图方法结合,并验证方法的有效性。总之,本研究在利用实地采样点对研究区土种类型进行推理的框架下,不仅探究了母质类别对环境因子选择的影响,同时也提出了新的制图方法将环境因子关联关系融入到土壤类型推理中,为数字土壤制图提供了新的制图思路。
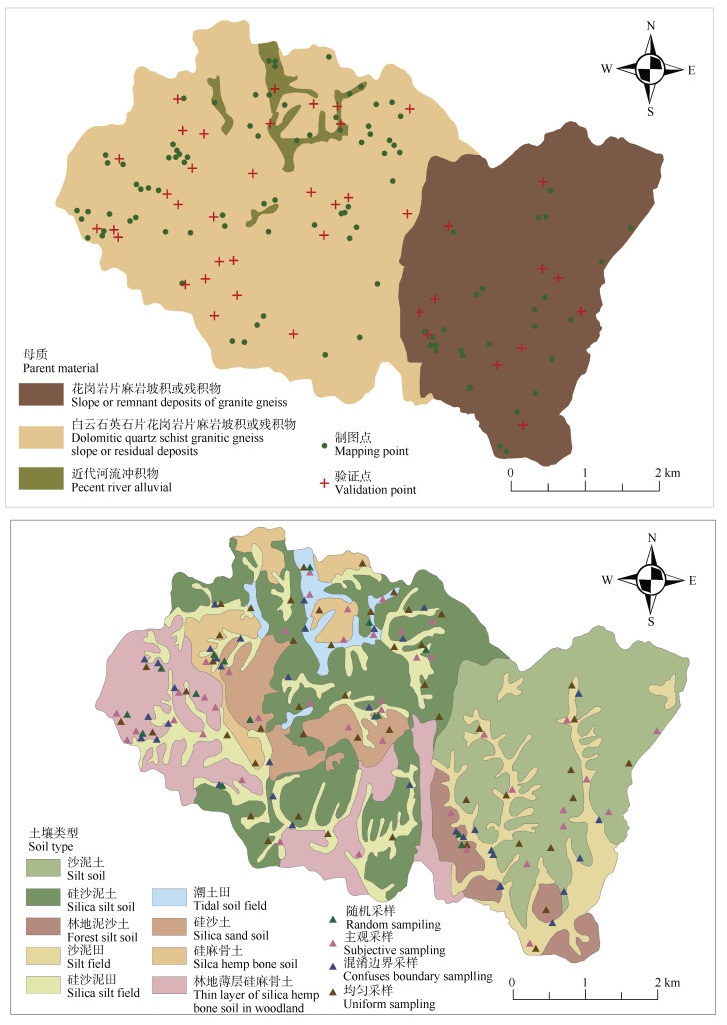
1 材料与方法 1.1 研究区概况研究区位于湖北省麻城市乘马岗镇,总面积约为28.14 km2,研究区中心地理坐标为31°25′30″N,114°58′30″E,高程介于80~346 m之间。乘马岗镇是一个山区农业乡镇,属于亚热带湿润季风气候,全镇地势北高南低,研究区共有3种母质类型,9种土壤类型,研究区的基础信息如图 1所示。
|
a. 母质及样点分布图 b. 土壤类型及采样点分布图 a. Map of parent material and sample sites b. Map of soil types and sampling sites 图 1 研究区基础信息图 Fig. 1 Basic information map of the study area |
研究区由花岗岩-片麻岩坡积或残积物、白云石英片岩-花岗片麻岩坡积或残积物以及近代河流冲积物等3种母质构成,母质信息来源于湖北省第二次土壤普查数据。本研究的样本数据通过完全随机采样、主观采样、混淆区域边界采样和均匀采样(网格采样)等4种方式相结合共采集实地样点141个,采样时间为2020年10月—2021年6月,根据分层随机抽样方法将其分为100个制图点和41个验证点[15],研究区各土壤类型对应的母质及样点个数信息如表 1所示。
|
|
表 1 土壤类型样点分布 Table 1 Sample distribution of soil type |
在研究区内,近代河流冲积物母质上仅有潮土田一种土壤类型,且面积占比较小,故在分区建模时将此区域与白云石英片岩-花岗片麻岩坡积或残积物母质区域合并研究。地形因子和遥感因子作为预测变量进行土壤类型推理被证明是可行且精度高的[16]。本研究使用了地形和遥感共计18个因子,地形数据来源于湖北省测绘局的等高线数据,利用ArcGIS10.8软件生成10 m分辨率的数字高程模型(DEM),继而得到高程(Elevation)、坡度(Slope)、坡向(Aspect)、平面曲率(Plan curvature)、剖面曲率(Profile curvature)、地形湿度指数(Topographic wetness index,TWI)、地形起伏度(Relief Degree of Land Surface)、地表粗糙度(Surface Roughness)等8个地形因子。遥感数据通过欧空局(ESA)官网获取2021年12月10日的Sentinel-2A遥感影像(云量较低、地表植被覆盖度适中),通过ENVI5.3软件对遥感影像处理得到归一化植被指数(Normalized differential vegetation index,NDVI)、第一主成分(First principal component,FPC)以及均值(Mean)、方差(Variance)、协同性(Homogeneity)、对比度(Contrast)、相关性(Correlation)、相异性(Dissimilarity)、信息熵(Entropy)、二阶矩(Second Moment)8个纹理信息等共计10个遥感因子,获取的18个环境因子用于后续因子筛选。
1.3 研究方法 1.3.1 基础方法基于随机森林的递归特征消除算法被证明较适用于土壤类型推理,而且该方法可以评估因子的重要性[17]。本研究采用此方法按照母质类型分别筛选最合适的环境因子用于制图,并与未按母质类型筛选环境因子的制图结果进行比较。
随机森林算法、基于C5.0决策树的SoLIM方法、KNN算法均能对土壤类型推理预测。随机森林算法在土壤类型或属性预测方面均得到了广泛应用并展现出了优越性能[18-19],这得益于其两次的随机选择并建立多个决策树(随机选取样本点和随机选择特征子集),增加了模型的多样性[20],但是随机选择就会产生误差,如何既保留算法的多样性,又降低其随机性带来的误差,成为了随机森林进一步发展的瓶颈;SoLIM方法通过隶属度函数得到各环境因子的隶属度,再根据限制因子学原理确定环境因子组合相似度,继而利用模糊最大算子确定空间内各点的土壤相似度,将相似度硬化,最终得到该区域的土壤图[6],该方法在对像元土壤类型判定时,某一影响程度最大的环境因子能够更多地决定该像元的土壤类型;KNN算法简单地利用预测点与已知类别点之间的距离远近进行土壤类型的推理[21]。因此,对于三种方法而言,若能在其推理预测中加入每种土壤类型对应的环境因子内部关联关系,即可以更好地弥补由于制图推理原理本身形成的不足。
1.3.2 结合方法频繁项集即频繁出现在数据集中的集合,具体是指在数据集中出现的频率不低于用户指定阈值的集合/项集,能够表示挖掘数据中的相关性、关联关系等[22]。在进行频繁项集挖掘前,参考关于低频关联信息挖掘的分级方式[23],并结合分级结果挖掘的频繁项集最终确定将研究区的各环境因子使用自然间断点分级法分为5级,每个级别对应一个编号,由于因子过多,仅展示部分分级结果,如表 2所示。将环境因子数据分级是挖掘环境因子关联信息的基础,例如挖掘结果显示某种土壤类型挖掘的频繁项集为(d2,s1)的含义为:该土壤类型在研究区常分布在高程为133.94~167.6,坡度为0~3.97的范围内,(d2,s1)即为该土壤类型的典型环境因子组合,可以用来反映环境因子的关联关系。
|
|
表 2 各环境因子数据范围分级 Table 2 Environmental factors data range grading |
对于本研究在数据分级时使用的是整体区域像元点的18个环境协变量,而非样本点对应的协变量数据用于分类统计做如下解释:(1)由于预测制图的对象是研究区整体,样本点数据并不能全部覆盖各种环境因子数值上下限,且样点数量较少时,统计分类结果可能未必精确。(2)有研究在进行土壤样本代表性修正时,将样本点的环境因子朝着与研究区整体环境因子更相近的方向进行样本代表性修正[24],表明整体区域的环境因子更能体现土壤的空间变化。
FP-Growth算法是目前常用的关联关系挖掘算法之一,采用树的结构遍历两次完成频繁项集挖掘[25]。在该算法中,某个频繁项集关联关系的强弱主要通过支持度和置信度来衡量,支持度表示该频繁项集在所有历史交易数据中同时出现的次数,置信度表示在某个频繁项集出现的情况下,另一个项出现的概率[21],即关联关系。为了进一步获取更加准确的频繁项集,本研究参考邱小倩等[23]关于衡量耕地质量数据库低频关联关系的指标公式,提出关于土壤类型分类频繁项集高频出现的过滤公式,称为误分概率P。误分概率越大,表示该种频繁项集越不容易将这种土壤类型误分给其他类,具体公式表达如下:
| $ \text{P=}\frac{频繁项集在一种土壤类型中出现的次数}{此频繁项集在所有土壤类型中出现的次数} $ | (1) |
本研究将FP-Growth算法挖掘到的频繁项集,经误分概率筛选和排序后与文中使用的机器学习制图方法相结合,再次推理制图。数据的预处理流程如下:获取各种制图方法的推理结果,将制图结果的所有像元转为矢量点,继而提取研究区环境因子分级结果至点,且与每个像元点的预测土壤类型一一对应,形成制图结果环境因子分级数据集,以和利用采样点挖掘的每种土壤类型的频繁项集数据进行匹配判断。
在结合方法中,每个像元最终土壤类型确定的核心即判断制图点筛选后的每种土壤类型的频繁项集分级结果(a)是否是全局每个像元点的环境因子分级结果(b)的子集,具体过程如下:(1)设某个像元的土壤类型为A,读取该像元对应的b,检索土壤类型A挖掘的a,判断土壤类型A的所有a是否是该像元对应b的子集,若是,则判定此像元的最终土壤类型为A;若不是,则依次判断其他土壤类型的a是否是该像元对应b的子集,若是,则将a对应的土壤类型赋予该像元,完成该像元最终的土壤类型判断。(2)若遍历了所有土壤类型的a,均未找到某个a是该像元对应b的子集,则将此像元的土壤类型判定为原类型A,完成该像元的土壤类型判断。依次对全局的所有像元根据此流程进行土壤类型的再次判定,即完成频繁项集与某种制图方法相结合的过程。
1.3.3 精度验证本研究基于41个验证点使用混淆矩阵以及Kappa系数对制图结果进行精度评价,各土壤类型精度通过混淆矩阵的用户精度和生产精度评价,整体制图效果使用总体精度以及Kappa系数衡量。Kappa系数通常在0~1之间,当Kappa系数在0~0.2,0.2~0.4,0.4~0.6,0.6~0.8,0.8~1时分别表示预测结果与实际结果一致性程度较差、一般、中等、较强和很强[26]。
2 结果与讨论 2.1 环境因子筛选高程、坡度、平面曲率、剖面曲率、地形湿度指数等5个指标在小区域内可以较好地反映土壤的发生和形成[27-28],本研究将这5个因子作为确定性环境因子直接参与制图,不再进行筛选。环境因子经递归特征消除算法计算后的模型精度如图 3所示。
|
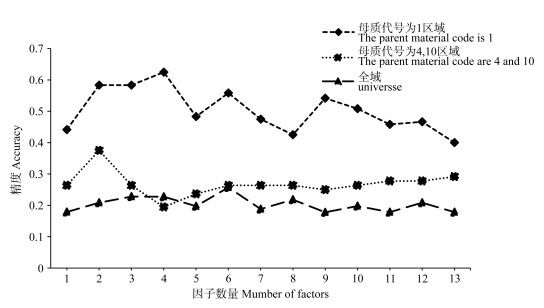
图 2 环境因子组合精度验证图 Fig. 2 Environmental factor combination accuracy verification diagram |
|
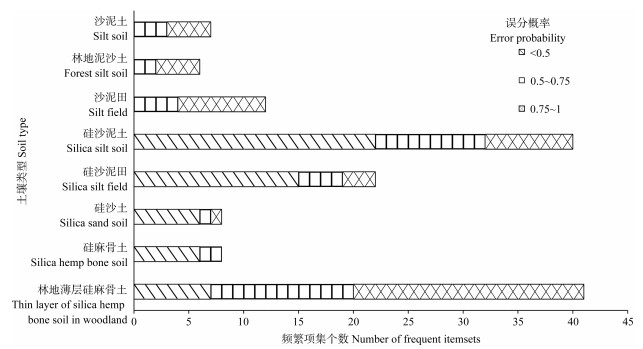
图 3 频繁项集个数统计 Fig. 3 The number of frequent itemsets |
由图 2可知全局、花岗岩-片麻岩坡积或残积物母质区域(代号1)、白云石英片岩-花岗片麻岩坡积或残积物和近代河流冲积物母质区域(代号4,代号10)的环境因子组合精度最高时对应的环境因子个数分别为6个、4个、2个,结合直接使用的5个环境因子,最终分别确定三种方式筛选和使用的具体环境因子结果见表 3。由图 2可知,母质花岗岩-片麻岩坡积或残积物区域的模型验证精度普遍高于母质为白云石英片岩-花岗片麻岩坡积或残积物和近代河流冲积物母质区域以及全局筛选时的模型精度,白云石英片岩-花岗片麻岩坡积或残积物和近代河流冲积物母质区域的模型精度整体上基本超过全局因子筛选的精度,表明将母质分开制图可能获得更好的效果。
|
|
表 3 筛选后环境因子汇总 Table 3 Summary of filtered environmental factors |
本研究使用FP-Growth算法挖掘100个制图点的环境因子分级数据,确定FP-Growth算法挖掘的最小支持度为3,置信度为1,即表示在所有样点中至少有3个及以上的样点同时拥有这种频繁项集组合。地理学第三定律提出:两点的地理环境越相似,土壤属性越相似[29]。于本研究而言,频繁项集出现的频次越高,越能代表某土壤类型的典型环境条件,即越可以用来推理土壤类型。在这一原则下,确定了频繁项集的置信度为1,即此环境因子组合一定会一起出现,为了尽可能使每种土壤类型均被挖掘到可以使用的频繁项集,确定了支持度为3。
由于挖掘的频繁项集数据较多,此处以某个频繁项集及其对应的误分概率为例进行阐述,如林地泥沙土挖掘的某个频繁项集为(m2,r3,p2),且误分概率为1,意味着此土壤类型在高程范围值为133.94~167.6,剖面曲率为-0.39~0.37,第一主成分为–208.02~267.74的环境因子组合下不会被误分为其他土壤类型。本研究获取所有土壤类型的频繁项集共计141个,经误分概率公式计算后统计,统计结果如图 3所示。
由图 3可知,部分土壤类型挖掘到了相对较多的频繁项集(如林地薄层硅麻骨土),除硅麻骨土外,其余几种土壤类型均挖掘到误分概率 > 0.75的频繁项集。因此本研究在不断试验并结合图 3统计结果的基础上最终确定将误分概率 > 0.75的频繁项集作为制图分类的依据(硅麻骨土使用误分概率最高的频繁项集),以获得相对准确的推理结果。
2.3 调参过程本研究在环境因子筛选时使用了递归特征消除算法,制图时分别使用了随机森林,基于C5.0决策树的SoLIM和KNN方法,其中基于C5.0决策树的SoLIM方法是通过Clementine软件挖掘规则集,并结合SoLIM软件实现土壤类型的推理,具体过程参考了韩浩武等[30]的研究。其余机器学习模型的调参过程均参考张晓婷等[17]的研究,各种算法调用及参数调节均依托于PyCharm2019软件编写python代码实现。
2.4 制图结果 2.4.1 基于所有母质直接制图结果本研究在利用全部母质直接制图时,经因子筛选、规则集建立等对整体研究区域制图。在将母质作为因子之一直接用于制图时使用12种环境因子分别通过随机森林算法、SoLIM方法、KNN算法进行研究区土壤类型的推理预测,推理预测的结果如图 4所示。
|
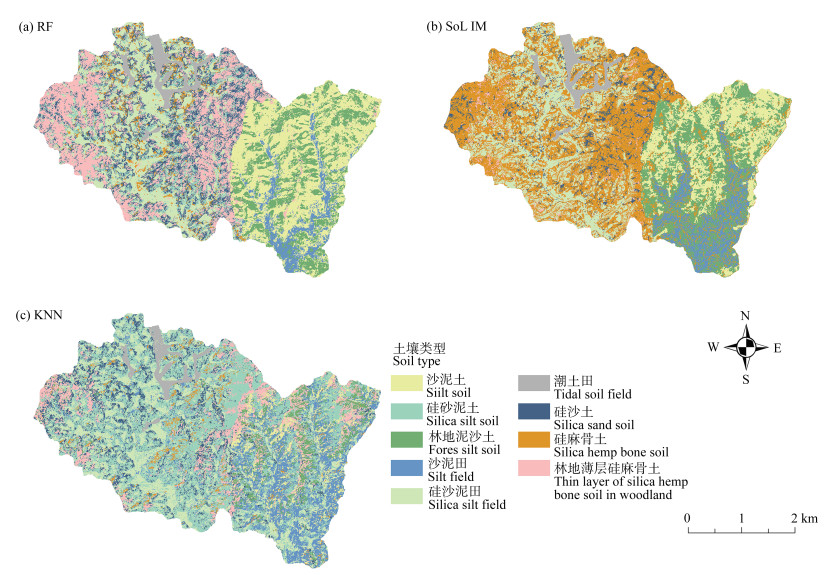
图 4 基于母质的不同方法土壤类型推理图 Fig. 4 Soil type inference figure based on parent material using different methods |
由图 4可知,三种制图方法对于某些土壤类型的预测在空间分布上是相似的,但是仍有部分土壤类型预测差异明显,其中KNN算法预测结果各土壤类型交错分布现象最为严重。随机森林和SoLIM方法预测有明显差异的为硅麻骨土,据该区域原始土壤图记载硅麻骨土在研究区内的分布面积相对较小(湖北省第二次土壤普查数据),即SoLIM方法预测此土壤类型有较高的错误率。三种制图方法的结果具有一个共同点,即在某一母质区域内均出现了不属于该母质发育而来的土壤类型,这也表明将母质分开制图是有必要的。
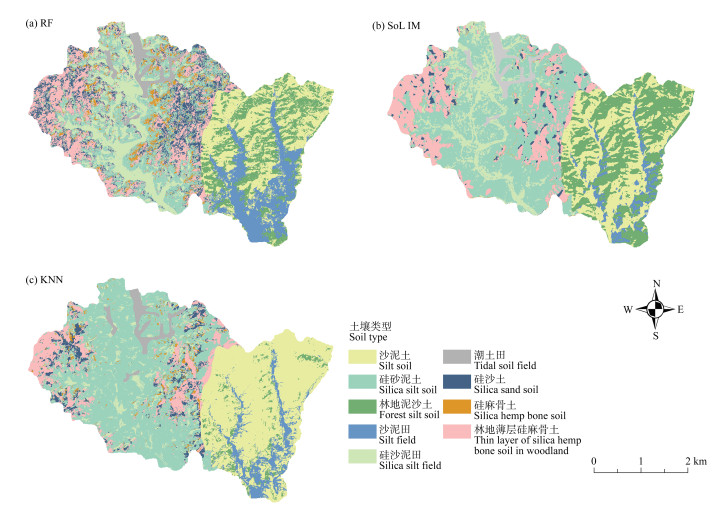
2.4.2 基于母质类别制图结果按照母质类别分别筛选环境因子并制图的推理结果如图 5所示。三种制图方法中SoLIM方法预测结果更加集中连片,这也与该方法的推理原理有一定关系,但是很少预测出硅麻骨土,对于硅砂土的预测也较为零散。随机森林对各土壤类型的推理相对均衡。KNN算法预测结果中,硅沙泥田并未被集中连片的预测,硅砂泥土被预测出了较大区域,硅麻骨土和林地泥沙土均被预测出较少面积。三种制图方法在母质花岗岩-片麻岩坡积或残积物区域的推理精度明显要好于其他母质区域的推理结果,这也与图 2因子筛选时得到的模型精度相符;在母质白云石英片岩-花岗片麻岩坡积或残积物和近代河流冲积物区域,随机森林和SoLIM方法的预测结果更为相似,在研究区的中部均预测出了硅沙泥田和硅砂泥土,三种方法在东部和西部分别推理出了林地薄层硅麻骨土。总之,三种制图方法在某些土壤类型推理上得到较为相似的分布预测,种类较未按母质类型制图时多,且各方法的推理结果更加集中连片,更能反映土壤的空间分布特征。同时,按照母质类型制图很大程度地避免了在某种母质区域内推理出不属于该母质发育而来的土壤类型的问题。所以,在使用实地采样点进行多母质区域的数字土壤制图时,应考虑母质类别进而选择最合适的环境因子进行推理预测。
|
图 5 基于母质类别的不同方法土壤类型推理图 Fig. 5 Inference map of soil types based on different parent materials type |
根据母质类别分别筛选环境因子进行制图是本研究的探索方向之一,但该方法也有一定的弊端。这是因为在相邻土壤的边界处往往呈现一定程度的过渡带,过渡带兼具两种土壤类型的属性[6],因此,在母质交界处,土壤类型的过渡带可能不能被很好的推理。但在利用100个采样点进行土壤类型推理时,将母质作为一种预测因子直接参与推理会降低母质在所有数据集中的重要性,这也可以解释图 4中的某一母质区域内预测出不属于该母质发育而来的土壤类型的现象(且并不处于两种母质交界处),可能当采样点数量足够多时,数据集会更好地反映母质在其中的重要性,进而减少这种现象的出现。
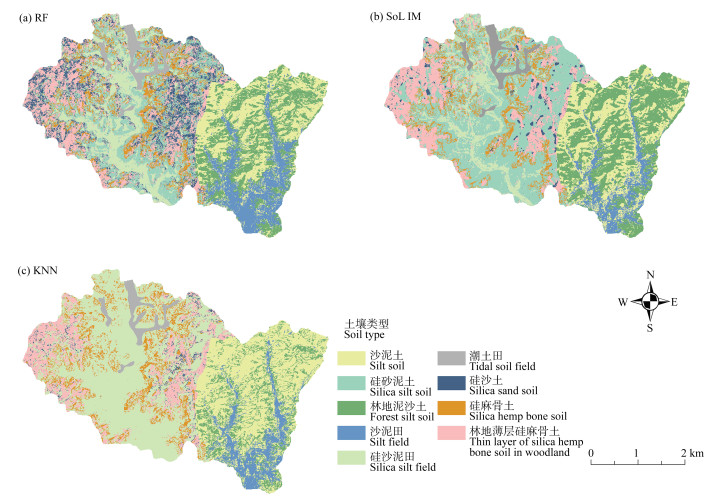
2.4.3 基于结合型方法制图结果本研究通过设计结合频繁项集的流程对研究区土壤类型再次推理,制图结果如图 6所示。随机森林对各土壤类型均预测出一定面积并显示更多细节。SoLIM方法预测硅沙土面积较小,硅砂泥土面积较大,结合频繁项集后,硅麻骨土预测面积增加,硅砂泥土预测面积减少。KNN算法预测结果中硅麻骨土和硅砂泥土的变化最为明显,结合频繁项集后,推理图预测出更多林地泥沙土和硅沙泥田,其空间分布更接近其他两种算法的预测结果。结合后的三种方法与未结合频繁项集的制图结果相比在整体分布上并未有明显差距,具体变化体现在三种方法均将硅麻骨土预测出了一定面积,且精度最差的KNN方法的部分土壤类型空间分布在朝着与另外两种方法制图结果更相似的方向推理。总之,三种制图方法结合频繁项集后对整体区域推理均有一定的改善。由三种制图模型的推理原理可知,其在确定土壤类型时对环境因子内部关联关系考虑较少,本研究在推理制图时融入关联关系,从原理上降低了预测误差。
|
图 6 结合典型环境因子的不同方法土壤类型推理图 Fig. 6 Soil type inference figure based on different methods combined with typical environmental factors |
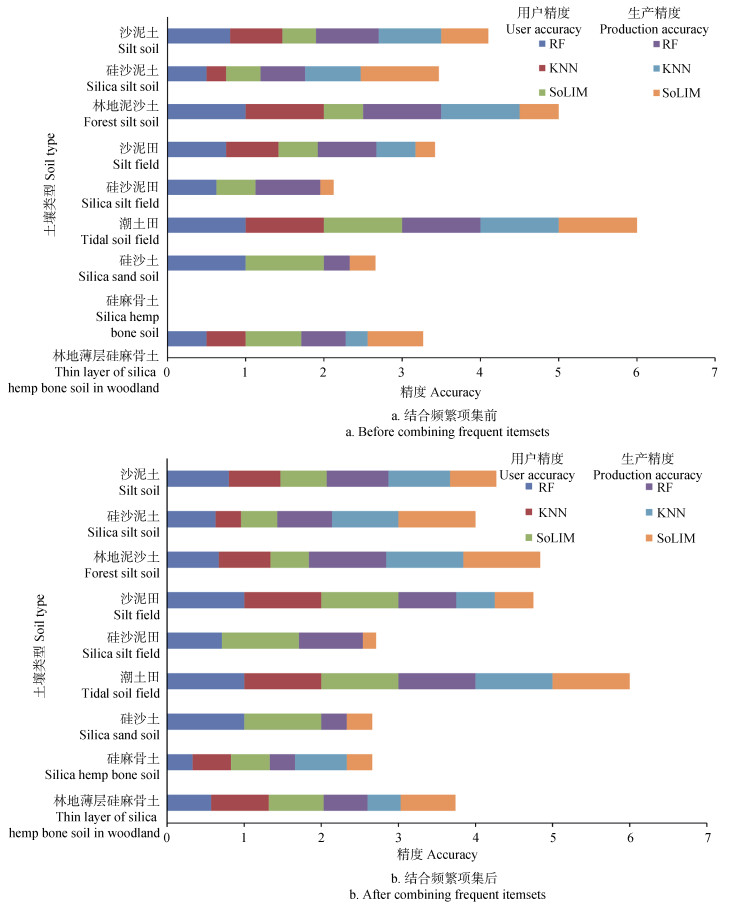
由图 4可知,在使用实地采样点推理制图时,三种制图结果均出现了在某种母质区域内推理出并非该母质发育而来的土壤类型的现象,并且KNN算法和SoLIM方法的预测结果并不理想,因此不再分析其具体土壤类型的预测精度,仅对按母质类别制图以及结合方法制图的土壤类型进行精度分析,各土壤类型用户精度和生产精度如图 7所示。
|
图 7 各土壤类型用户精度和生产精度统计图 Fig. 7 Statistical figure of user accuracy and production accuracy of each soil type |
由图 7可知,硅麻骨土的推理结果并不理想,三种制图方法均未较好地预测该土壤类型,这可能是因为该土壤类型在研究区内不仅面积小,而且据《麻城市土壤志》(内部资料1983)记载该土壤类型的地理环境描述与其他土壤类型也较为相似。频繁项集结合前后推理精度最高的依然为潮土田(100%),这主要是因为研究区内近代河流冲积物母质区域仅有此种土壤类型,不易误分。与频繁项集结合后的其他土壤类型各种推理方法的用户精度与生产精度累积长度均表现为不变或增加,这表明了将环境因子关联关系融入到制图当中的可靠性,验证了本研究制图方法的有效性。各种方法制图总效果通过总精度和Kappa系数衡量,具体结果见表 4。
|
|
表 4 各制图方法总体效果评价 Table 4 Evaluation of the overall effect of each mapping method |
表 4显示,三种方法按母质类型的制图精度均较未按母质类型制图的精度和Kappa系数高,结合了频繁项集的制图方法均较未结合的总精度和Kappa系数高。是否按母质类型制图对SoLIM方法的影响最大,这可能是因为C5.0决策树在进行规则挖掘时因子较多,样本点较少,挖掘的规则并不特别适合SoLIM方法,且SoLIM方法在进行硬化时[31],影响程度最大的某个因子很大程度上决定了土壤类型的判定,结合图 4b可知,硅麻骨土的因子规则很大程度影响了其他土壤类型的因子规则。然而,将母质分开制图时,使用的因子减少,且避免了某些因子之间的相互影响。因此,在进行少量样点(统计意义)的土壤制图时需考虑母质类型对环境因子的影响。
在所有方法中,结合频繁项集的随机森林制图精度最高,为70.73%。最低的为母质一起制图时KNN算法的制图结果,为43.9%。由结合频繁项集的精度可知,结合前后验证点的制图精度均为:随机森林 > SoLIM > KNN,结合频繁项集后,KNN算法总精度和Kappa系数均提升最多,分别提升了9.76%和11.70%。这主要是因为该算法的原始制图精度较低,故其提升空间相对较大。随机森林提升的效果最低,一方面是因为其本身精度较高,另一方面是因为其在随机选取特征子集时建立了多个决策树,在一定程度上也可以弥补这种误差。同时,本研究设计的结合方法是在原始制图结果的基础上进一步判断的,所以在一定程度上依赖于原制图方法,但从总精度和Kappa系数来看,本研究提出的结合制图方法是有效且实用的。
对于本研究提出的频繁项集与三种制图模型结合的方法而言,结合后三种方法的制图精度均有提升,这也是符合方法推理逻辑的,但是是否适合数字土壤制图中的其他方法仍需不断验证。并且,本研究某些土壤类型并未挖掘到频繁项集误分概率为100%的组合,可能增加相应土壤类型的采样点获取更多挖掘信息,即可以获取分类精度更高的频繁项集,从而更好地推理土壤类型的空间分布。
3 结论本研究通过递归特征消除算法按母质类别筛选环境因子,探究了不同制图方法下母质类别对环境因子筛选的影响。继而将频繁项集分别与不同制图结果结合,验证了本研究提出方法的有效性。随机森林与频繁项集结合推理的精度最高(70.73%),推理结果能较好地描述研究区土壤类型的大致空间分布,可以为农业生产、土地保护等提供参考。
按母质类型制图时,不同方法的制图效果和预测精度均较将母质一起直接制图时好,制图结果更加集中连片,土壤类型空间分布更为合理。精度评价结果显示,不同结合型制图方法的精度均高于未结合时方法的精度,其中提升最多的是KNN方法,最少的为随机森林方法,验证了本研究提出方法的有效性以及使用FP-Growth算法挖掘典型环境因子组合的可靠性。本研究不仅为基于实地采样点进行多母质区域土种类型的环境因子筛选提供了参考,同时也为数字土壤制图提供了新的制图思路和方法,有利于更好地服务农业数字化和信息化。
| [1] |
Zhu A X, Yang L, Fan N Q, et al. The review and outlook of digital soil mapping (In Chinese)[J]. Progress in Geography, 2018, 37(1): 66-78. [朱阿兴, 杨琳, 樊乃卿, 等. 数字土壤制图研究综述与展望[J]. 地理科学进展, 2018, 37(1): 66-78.]
(  0) 0) |
| [2] |
Zhu A X, Li B L, Yang L, et al. Predictive soil mapping based on a GIS, expert knowledge, and fuzzy logic framework and its application prospects in China (In Chinese)[J]. Acta Pedologica Sinica, 2005, 42(5): 844-851. DOI:10.3321/j.issn:0564-3929.2005.05.019 [朱阿兴, 李宝林, 杨琳, 等. 基于GIS、模糊逻辑和专家知识的土壤制图及其在中国应用前景[J]. 土壤学报, 2005, 42(5): 844-851.]
(  0) 0) |
| [3] |
Huang W, Luo Y, Wang S Q, et al. Knowledge of soil-landscape model obtain from a soil map and mapping (In Chinese)[J]. Acta Pedologica Sinica, 2016, 53(1): 72-80. [黄魏, 罗云, 汪善勤, 等. 基于传统土壤图的土壤—环境关系获取及推理制图研究[J]. 土壤学报, 2016, 53(1): 72-80.]
(  0) 0) |
| [4] |
Mehrabi Gohari E, Matinfar H R, Taghizadeh R. Evaluating soil-environment inference model(SOLIM)for soil mapping based on fuzzy logic in Kashan[J]. Journal of Water and Soil Science, 2017, 21(3): 255-268. DOI:10.29252/jstnar.21.3.255
(  0) 0) |
| [5] |
Zhou Y, Zhao X M, Guo X. Prediction of total nitrogen distribution in surface soil based on multi-source auxiliary variables and random forest approach (In Chinese)[J]. Acta Pedologica Sinica, 2022, 59(2): 451-460. [周洋, 赵小敏, 郭熙. 基于多源辅助变量和随机森林模型的表层土壤全氮分布预测[J]. 土壤学报, 2022, 59(2): 451-460.]
(  0) 0) |
| [6] |
Zhu A X. Model and method of fine digital soil survey (In Chinese). Beijing: Science Press, 2008. [朱阿兴. 精细数字土壤普查模型与方法[M]. 北京: 科学出版社, 2008.]
(  0) 0) |
| [7] |
Gong Z T. China soil geography (In Chinese). Beijing: Science Press, 2014. [龚子同. 中国土壤地理[M]. 北京: 科学出版社, 2014.]
(  0) 0) |
| [8] |
Huang W, Xu W, Wang S Q, et al. Extraction of knowledge about soil-environment relationship based on an uncertainty model (In Chinese)[J]. Acta Pedologica Sinica, 2018, 55(1): 54-63. [黄魏, 许伟, 汪善勤, 等. 基于不确定性模型的土壤——环境关系知识获取方法的研究[J]. 土壤学报, 2018, 55(1): 54-63.]
(  0) 0) |
| [9] |
Lagacherie P. Digital soil mapping: A state of the art[M]//Digital soil mapping with limited data. Dordrecht: Springer Netherlands, 2008: 3—14.
(  0) 0) |
| [10] |
Wadoux A M J C, Minasny B, McBratney A B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions[J]. Earth-Science Reviews, 2020, 210: 103359. DOI:10.1016/j.earscirev.2020.103359
(  0) 0) |
| [11] |
Chen R. Soil mapping method research in mixing region of plain and hill[D]. Wuhan: Huazhong Agricultural University, 2021.[陈荣. 平原-丘陵混合区域土壤制图方法研究[D]. 武汉: 华中农业大学, 2021.]
(  0) 0) |
| [12] |
Pekel E. Estimation of soil moisture using decision tree regression[J]. Theoretical and Applied Climatology, 2020, 139(3): 1111-1119.
(  0) 0) |
| [13] |
Hateffard F, Dolati P, Heidari A, et al. Assessing the performance of decision tree and neural network models in mapping soil properties[J]. Journal of Mountain Science, 2019, 16(8): 1833-1847. DOI:10.1007/s11629-019-5409-8
(  0) 0) |
| [14] |
Chandan T R. Recent trends of machine learning in soil classification: A review[J]. International Journal of Computational Engineering Research, 2018, 8(9): 2250-3005.
(  0) 0) |
| [15] |
Huang S H, Pu L J, Xie X F, et al. Review and outlook of designing of soil sampling for digital soil mapping (In Chinese)[J]. Acta Pedologica Sinica, 2020, 57(2): 259-272. [黄思华, 濮励杰, 解雪峰, 等. 面向数字土壤制图的土壤采样设计研究进展与展望[J]. 土壤学报, 2020, 57(2): 259-272.]
(  0) 0) |
| [16] |
Duan M Q, Zhang X G. Using remote sensing to identify soil types based on multiscale image texture features[J]. Computers and Electronics in Agriculture, 2021, 187: 106272.
(  0) 0) |
| [17] |
Zhang X T, Huang W, Fu P H, et al. Research on digital soil mapping based on feature screening algorithm (In Chinese)[J]. Acta Pedologica Sinica, 2024, 61(3): 635-647. [张晓婷, 黄魏, 傅佩红, 等. 基于特征筛选算法的数字土壤制图研究[J]. 土壤学报, 2024, 61(3): 635-647.]
(  0) 0) |
| [18] |
Zhou Z K, Wang Z Q, Wang W, et al. Spatial distribution simulation of soil heavy metals based on remote sensing data and random forest algorithm—Taking chromium as an example (In Chinese)[J]. Journal of Anhui Agricultural Sciences, 2023, 51(14): 51-54. [周忠科, 王泽强, 王唯, 等. 基于遥感数据和随机森林算法的土壤重金属空间分布模拟——以铬为例[J]. 安徽农业科学, 2023, 51(14): 51-54.]
(  0) 0) |
| [19] |
Zhang Y K, Ji W J, Saurette D D, et al. Three-dimensional digital soil mapping of multiple soil properties at a field-scale using regression Kriging[J]. Geoderma, 2020, 366: 114253.
(  0) 0) |
| [20] |
Zhou Z H. Machine learning (In Chinese). Beijing: Tsinghua University Press, 2016. [周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.]
(  0) 0) |
| [21] |
Kotu V, Deshpande B. Predictive analytics and data mining: Concepts and practice with RapidMiner . Waltham, MA: Morgan Kaufmann, 2015.
(  0) 0) |
| [22] |
Zhu X, Deng H T, Chen Z. A brief review on frequent pattern mining[C]//2011 3rd International Workshop on Intelligent Systems and Applications. Wuhan, China. IEEE, 2011: 1—4.
(  0) 0) |
| [23] |
Qiu X Q, Hu Y M, Zhu A X, et al. Research on associated rule-based error checking method on assessment index database of cultivated land quality: A case study on Guangzhou city (In Chinese)[J]. China Land Science, 2020, 34(3): 75-83. [邱小倩, 胡月明, 朱阿兴, 等. 基于关联规则的耕地质量评价数据检错方法研究——以广州市为例[J]. 中国土地科学, 2020, 34(3): 75-83.]
(  0) 0) |
| [24] |
Zhang G M, Zhu A X. A representativeness heuristic for mitigating spatial bias in existing soil samples for digital soil mapping[J]. Geoderma, 2019, 351: 130-143.
(  0) 0) |
| [25] |
Han J W, Pei J, Yin Y W, et al. Mining frequent patterns without candidate generation: A frequent-pattern tree approach[J]. Data Mining and Knowledge Discovery, 2004, 8(1): 53-87.
(  0) 0) |
| [26] |
Bai H R, Zhao M F, Wang F, et al. Prediction and mapping of Stagnic Anthrosols soil series based on fuzzy c-means algorithm (In Chinese)[J]. Journal of Nanjing Agricultural University, 2020, 43(6): 1124-1133. [白浩然, 赵美芳, 王飞, 等. 基于模糊c-均值算法的水耕人为土土系预测制图[J]. 南京农业大学学报, 2020, 43(6): 1124-1133.]
(  0) 0) |
| [27] |
McSweeney K, Slater B K, David Hammer R, et al. Towards a new framework for modeling the soil-landscape continuum[M]//Amundson R, Harden J, Singer M, eds. SSSA Special Publications. Madison, WI, USA: Soil Science Society of America, 2015: 127—145.
(  0) 0) |
| [28] |
Qiu L, Li A B, Zhao Y G. Digital soil mapping based on Fisher discriminant analysis (In Chinese)[J]. Chinese Journal of Soil Science, 2012, 43(6): 1281-1286. [邱琳, 李安波, 赵玉国. 基于Fisher判别分析的数字土壤制图研究[J]. 土壤通报, 2012, 43(6): 1281-1286.]
(  0) 0) |
| [29] |
Zhu A X, Lu G N, Liu J, et al. Spatial prediction based on third law of geography[J]. Annals of GIS, 2018, 24(4): 225-240.
(  0) 0) |
| [30] |
Han H W, Xu W, Huang W, et al. Soil mapping based on remote sensing images and decision tree algorithm (In Chinese)[J]. Chinese Journal of Soil Science, 2019, 50(1): 8-14. [韩浩武, 许伟, 黄魏, 等. 基于遥感影像和决策树算法的土壤制图[J]. 土壤通报, 2019, 50(1): 8-14.]
(  0) 0) |
| [31] |
Zhu A X, Hudson B, Burt J, et al. Soil mapping using GIS, expert knowledge, and fuzzy logic[J]. Soil Science Society of America Journal, 2001, 65(5): 1463-1472.
(  0) 0) |
 2025, Vol. 62
2025, Vol. 62


