2. 北京林业大学水土保持学院, 北京林业大学水土保持国家林业和草原局重点实验室, 北京 100083;
3. 广西水利电力职业技术学院, 南宁 530023
2. School of Soil and Water Conservation, Key Laboratory of State Forestry and Grassland Administration on Soil and Water Conservation, Beijing Forestry University, Beijing 100083, China;
3. Guangxi Vocational College of Water Resources and Electric Power, Nanning 530023, China
土壤侵蚀是一个全球性的环境问题[1],会造成耕层土壤流失,降低耕地质量,严重威胁农业可持续发展[2-3]。细沟侵蚀是坡耕地土壤侵蚀的主要形式之一。集中水流引起的细沟侵蚀是坡面侵蚀的主要来源,也是泥沙运移的主要渠道[4],在黄土高原地区其侵蚀量占坡面侵蚀量70%以上[5]。现如今,细沟侵蚀已然成为制约黄土高原农业生产的一个重要因素,深入研究细沟侵蚀过程对该区域坡耕地土壤侵蚀预报和综合防治具有重要现实意义。
微地形是影响土壤侵蚀演变的关键因素,它通过改变径流侵蚀力,进而影响侵蚀的演变过程和泥沙的产生量[6]。在侵蚀作用下,坡面土壤在径流和泥沙运动过程中不断被剥离、搬运和沉积,这一过程推动着地表微地形的演变[7]。目前用于描述小尺度地表微地形的宏观因子主要包括地表粗糙度、地形起伏度、地表切割深度等[8-9]。李龙等[10]在自然降雨条件下通过野外径流小区监测试验,研究了水力侵蚀下砒砂岩坡面微地貌变化及其与产流产沙的关系,表明地表粗糙度与径流量、泥沙量呈显著正相关性。Zhang等[11]在模拟降雨条件下研究了4个常规耕作边坡的空间异质性,发现土壤表面粗糙度增加了径流阻力,降低了径流速度,从而降低了径流剪切力和泥沙负荷能力,减少了土壤侵蚀。梁心蓝等[12]设置了4种不同初始糙度的坡面,通过室内模拟降雨试验,研究了初始地表糙度对径流水力学特征和侵蚀的影响,发现相同雨强和降雨历时下,初始粗糙度越大的坡面,其径流量和产沙量越小,且在初始粗糙度极小的直型坡面,径流的雷诺数越大,地表糙度增大幅度也更大。综上,地表微地形与土壤侵蚀相互关联,地表微地形不仅是侵蚀的直接结果,还是侵蚀进一步发展的原因。土壤侵蚀过程与水流水力学特征参数(流速、雷诺数、弗劳德数等)有着密切联系,水流形态随侵蚀持续发生变化,同时直接影响侵蚀阶段微地形的演变。前人的研究聚焦于坡面初始微地形与土壤侵蚀的关系,很少关注侵蚀重塑引起的地表微地形与水流水力学特征参数之间的关系,侵蚀重塑引起的地表微地形变化及其对水力学特征参数的响应关系尚不明确,影响了对侵蚀机理的深入理解。因此,探究侵蚀后地表微地形的变化及其对水力学特征参数的响应关系对深入分析坡面细沟侵蚀过程和机制具有重要意义。
饱和土壤作为细沟侵蚀发生的众多下垫面条件之一,其具有较高的土水势,水土流失更严重。几种特定条件均会造成土壤饱和,例如,传统耕作方式使耕层底部形成犁底层,其土壤透水性差,在极端降雨或长历时降雨条件下,因犁底层入渗受阻,使耕层逐渐形成饱和土层[13]。同时,土壤发育类型呈A-C层结构特点,C层渗透性差。作物秸秆覆盖使得坡耕地表层土壤具有较高的蓄水和入渗能力,易达到饱和状态[14]。长期饱和状态下,土壤团聚体结构发生改变,如土壤颗粒之间的黏附性降低,土壤更易发生侵蚀[13]。黄绵土具有质地轻、土体松散、抗蚀性差等特点,是黄土高原分布面积最广泛的土壤类型。在全球气候变暖背景下,黄土高原地区夏季极端降水事件增多,且强度增大[15-16],坡耕地耕层土壤易出现饱和状态,水土流失强度加大。因此,本文以黄绵土为研究对象,通过室内放水冲刷试验,结合运动恢复结构摄影测量法,研究饱和黄绵土细沟侵蚀过程中水力学特征参数和侵蚀重塑引起的地表微地形变化规律,探究流速和雷诺数分别与地表粗糙度、地形起伏度和地表切割深度的耦合关系,阐明饱和黄绵土坡面细沟侵蚀重塑引起的微地形变化对水力学特征参数的响应,以期为黄绵土坡耕地水土流失的防治提供科学依据。
1 材料与方法 1.1 供试材料试验土壤为黄绵土,采集自中国陕西省延安市安塞水土保持综合试验站(36°51′30″N,109°19′23″E),采集深度为0~20 cm。通过吸管法测定土壤机械组成,其黏粒、砂粒和粉粒含量分别为10.82%、31.71%和57.47%,根据美国制土壤质地分类标准划分为粉质壤土。采用重铬酸钾法测定有机质含量为8.50 g·kg–1。
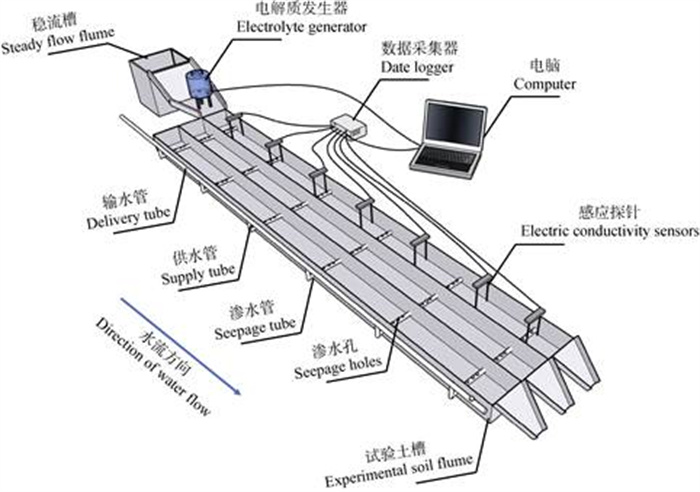
1.2 试验装置试验土槽长6 m,用PVC板分隔为3条长6 m、宽0.1 m和高0.35 m的限定性细沟(图 1)。每条细沟划分为6个1 m沟段,每沟段再分0.1 m和0.9 m两个单元。0.1 m单元内布设饱和供水装置,包括渗水管、供水管和输水管。两个单元底部压实装填3 cm厚黏土层,渗水管(d=1 cm)横向布设于土层上方,且贯穿3条细沟。每个渗水管侧边上等间距设有渗水孔(d=2 mm),使水流从底部供水至土壤,并用透水性好的土工织物包裹,防止渗水孔被土壤粗颗粒堵塞。供水管与渗水管垂直相连,且上端与试验土壤顶部处于同一水平高度,每根供水管配有阀门控制供水流量,其上端连接至一条输水管并直通水源。饱和装置及原理与Huang等[17]的一致,且研究已验证了该装置可以实现整个土壤坡面均达到饱和状态。
|
图 1 试验土槽示意图 Fig. 1 Experimental equipment diagram |
试验地点位于广西水利电力职业技术学院模拟降雨大厅。根据退耕还林临界坡度为25°,细沟发育的临界坡度为2°,且坡度超过5°时细沟发育广泛,因此本试验选取缓斜坡、斜坡与陡坡的代表性坡度,设置4个坡度:5°、10°、15°、20°。其次,黄土高原常见的短历时、高强度侵蚀性降雨标准为10.5~234.8 mm·h–1[18],设计4个集中水流流量为2、4、8、16 L·min–1,相当于在17 m汇水坡长、0.3 m坡宽、径流系数为0.8条件下分别发生25、59、118、235 mm·h–1降雨强度的侵蚀性降雨。冲刷时间为2 min,每个处理重复3次,共计48场冲刷试验。
1.4 试验步骤试验前,将土壤自然风干后过5 mm筛,以去除杂质。根据设计容重1.2 g·cm–3按式(1)计算出所需土样质量,分4层装填土壤,每层厚度为5 cm,每层间进行打毛处理,填土总高度为20 cm,用以模拟耕作层。
| $ {\mathit{m}} = B \times L \times {\mathit{b}} \times H \times (1 + w) $ | (1) |
式中,m为所需土样质量,kg;B为设计容重,g·cm–3;L为土槽长度,m;b为土槽宽度,m;H为填土高度,m;w为土壤含水量,%。
土壤装填完毕后打开饱和供水装置,供水至土壤完全饱和。土壤饱和后用相机对全坡面拍照,获取试验前地表微地形初始数据。调整土槽至设计坡度,通过蠕动泵标定流量,经稳流槽将水流引入饱和土壤表面进行冲刷。采用薄层水流流速测量系统测量并记录电解质在水流中的运动过程。6个感应探针分别放置于距离进水口0.2、1、2、3、4、5、6 m的位置,装有饱和KCL溶液的电解质发生器固定在距离进水口0.1 m处,通过计算机控制电解质注入水流,同时数据采集器开始记录电解质浓度数据。冲刷结束后,用相机对侵蚀坡面拍照以获取试验后的地表微地形数据。试验前后测定水温,取平均值用于计算运动黏滞系数。
1.5 水力学特征参数的计算(1) 电解质质心流速。假设电解质质心到达每个感应探针所需的时间等于水流经过每个感应探针的时间,由水流通过的距离和通过时间来计算水流的平均流速[19]。计算过程如下:
电解质质心从电解质发生器到每个感应探针的时间计算如下:
| $ {{\text{T}}_i} = \frac{{{\Sigma _j}{C_{ij}}{T_j}}}{{{\Sigma _j}{C_{ij}}}} \:\:\:\: i = 1,2,3... $ | (2) |
式中,Ti为电解质质心从电解质发生器到第i个感应探针所需的时间,s;Cij为第i个感应探针在Tj时的电解质浓度,kg·m–3;Tj为测量时间,s。
水流通过两个相邻感应探针的平均流速:
| $ {\overline V _i} = \frac{{\Delta {L_i}}}{{\Delta {T_i}}} $ | (3) |
式中,
(2) 雷诺数和弗劳德数。雷诺数(Re)和弗劳德数(Fr)为表征水流形态的无量纲参数。雷诺数是判定水流为层流或紊流的定量标准,弗劳德数用于判别水流的缓急。计算公式如下:
| $ {\mathit{h = }}\frac{{\mathit{Q}}}{{{\mathit{Vb}}}} $ | (4) |
式中,h为平均水深,m;Q为流量,m3·s–1;b为水流宽度,m。
| $ {\mathit{R = }}\frac{{bh}}{{b + 2h}} $ | (5) |
式中,R为水力半径,m。
| $ {\mathit{v = }}\frac{{0.01775 \times {{10}^{ - 4}}}}{{1 + 0.0337T + 0.000221{T^2}}} $ | (6) |
式中,v为运动黏滞系数,m2·s–1;T为水温,℃。
| $ {\mathit{Re = }}\frac{{VR}}{v} $ | (7) |
| $ {\mathit{Fr = }}\frac{V}{{\sqrt {gh} }} $ | (8) |
式中,g为重力加速度,m·s–2,取g=9.8 m·s–2。
(3) 阻力系数。因Darcy-weisbach阻力系数为无量纲参数而被广泛使用,表征坡面流阻力,计算公式如下:
| $ \lambda = \frac{{8{\text{g}}RJ}}{{{V^2}}} $ | (9) |
式中,λ为阻力系数;J为水力坡度,近似取sinθ,θ为土槽坡度。
1.6 微地形因子的提取与分析方法基于运动恢复结构(Structure-from-Motion,简称SfM)的摄影测量法测定不同处理下的微地形因子。将试验前后的照片导入Agisoft Photoscan Professional 1.8.5(Agisoft LLC)软件生成三维密集点云,将生成的密集点云导入到ArcGIS Pro 3.0.0(Esri Inc)软件生成地面高程模型(DEM)并校正。使用ArcToolbox的栅格数学工具计算全坡面内平均地表粗糙度,地形起伏度和地表切割深度选择5 cm×5 cm的矩形作为窗口,使用Matlab(The Mathworks Inc)软件进行批量分析获取。具体计算如下:
地表粗糙度
| $ RR = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {Z\left( {{X_i}} \right) - \overline Z } \right]}^2}} } $ | (10) |
式中,RR为随机粗糙度,mm;N为生成DEM中的网格数;Z(Xi)为网格Xi的高程,mm;
地形起伏度
| $ {\mathit{RA}} = {{\mathit{H}}_{{\mathit{max}}}} - {{\mathit{H}}_{\min }} $ | (11) |
式中,RA为地形起伏度,cm;Hmax和Hmin为分析窗口内高程最大值和高程最小值,cm。
地表切割深度
| $ {\mathit{SI = }}{{\mathit{H}}_{{\mathit{mean}}}} - {{\mathit{H}}_{{\text{min}}}} $ | (12) |
式中,SI为地表切割深度,cm;Hmean为分析窗口内高程平均值。
试验前地表微地形初始数据如表 1所示,不同水力工况下的地表粗糙度、地形起伏度和地表切割深度的初始值极差分别为0.08、0.05和0.07 cm,表明各组试验前的微地形变化的差异极小,可忽略人工填土导致的初始微地形差异。
|
|
表 1 不同水力工况下试验前的微地形因子特征值 Table 1 Characteristic values of microtopography factors before testing under different hydraulic conditions |
本研究使用SPSS Statistics 27.0(SPSS Inc)软件进行统计学分析,采用单因素方差分析(ANOVA)和最小显著性差异(LSD)检验各处理间的差异。使用Origin 2021(OriginLab Inc)软件进行相关性分析和图形绘制。表中数值为平均值±标准差。
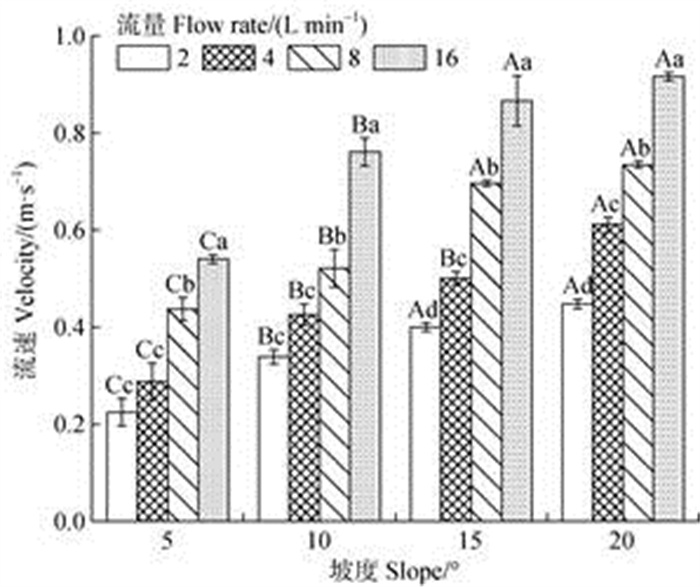
2 结果 2.1 水力学特征参数变化规律 2.1.1 流速不同水力工况下饱和黄绵土坡面细沟水流流速结果如图 2所示,其变化范围为0.23~0.92 m·s–1,且水流流速随坡度和流量的增大而增大(P < 0.05)。
|
注:不同大写字母表示在相同流量下不同坡度间差异显著(P < 0.05),不同小写字母表示在相同坡度下不同流量间差异显著(P < 0.05)。 Note:Different capital letters indicate the significance difference of different slopes at the same flow rate(P < 0.05),and different lowercase letters indicate the significance difference of different flow rates at the same flow rate(P < 0.05). 图 2 不同坡度和流量下流速变化 Fig. 2 Change of flow velocity under different slopes and flow rate |
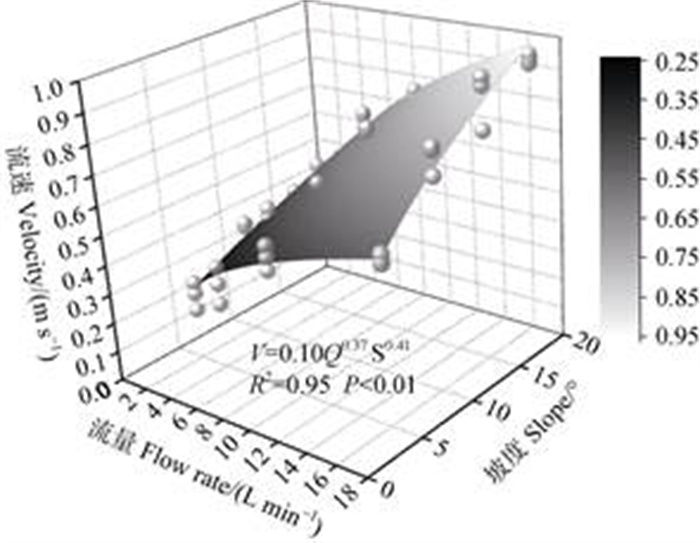
为确定流量和坡度对流速的影响程度,根据前人研究结果[20-21],本研究运用公式V=a·Qm·Sn对不同水力工况下的细沟流速进行拟合(图 3),其中决定系数R2为0.95,P < 0.01,坡度和流量的幂指数分别为0.41和0.37,表明饱和黄绵土坡面细沟水流流速可以用流量和坡度的幂函数较好地表示,且坡度对流速的影响更大。
|
图 3 饱和黄绵土细沟水流流速与坡度、流量的关系 Fig. 3 Relationship between flow velocity, slope, and flow rate of rill in saturated loess |
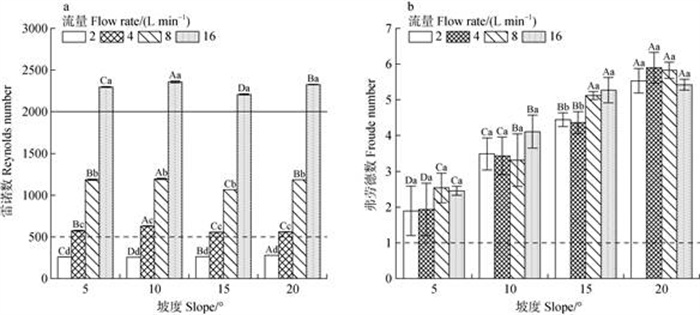
图 4为饱和黄绵土坡面细沟水流雷诺数和弗劳德数结果,由图 4a可知,当流量为2 L·min–1时,雷诺数为255~278,Re < 500,此时细沟水流为层流状态;流量为4和8 L·min–1时,雷诺数为557~629和1 065~1 196,为过渡流;流量为16 L·min–1时,雷诺数为2 208~2 358,Re > 2 000,属于紊流。弗劳德数的变化范围介于1.89~5.90之间(图 4b),所有试验处理下细沟水流Fr均大于1,属于急流范围。
|
注:a中虚线表示Re=500,实线表示Re=2 000;b中虚线表示Fr=1。不同大写字母表示在相同流量下不同坡度间差异显著(P < 0.05),不同小写字母表示在相同坡度下不同流量间差异显著(P < 0.05)。 Note:Dotted line in a indicates Re = 500,solid line indicates Re = 2 000;Dotted line in b indicates Fr = 1. Different capital letters indicate the significance difference of different slopes at the same flow rate(P < 0.05),and different lowercase letters indicate the significance difference of different flow rates at the same flow rate(P < 0.05). 图 4 不同坡度和流量下雷诺数(a)和弗劳德数(b)变化 Fig. 4 Change of Reynolds number(a)and Froude number(b)under different slopes and flow rate |
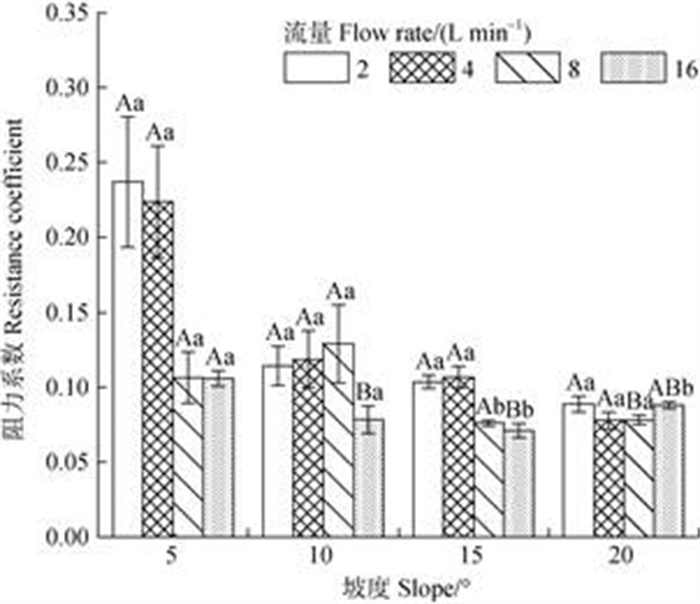
在试验条件下,细沟水流阻力系数变化范围为0.07~0.24(图 5)。除个别处理外(10°8 L·min–1和20°16 L·min–1),在相同流量下阻力系数随坡度增大而减小。坡度为5°和20°时,阻力系数整体上随着流量的增加而减小,而10°和15°坡度条件下阻力系数随流量增加呈先增大后减小的趋势。
|
注:不同大写字母表示在相同流量下不同坡度间差异显著(P < 0.05),不同小写字母表示在相同坡度下不同流量间差异显著(P < 0.05)。 Note:Different capital letters indicate the significance difference of different slopes at the same flow rate(P < 0.05),and different lowercase letters indicate the significance difference of different flow rates at the same flow rate(P < 0.05). 图 5 不同坡度和流量下阻力系数变化 Fig. 5 Change of resistance coefficient under different slopes and flow rate |
微地形因子的变化反映了坡面细沟侵蚀程度,是冲刷径流携带泥沙的共同作用导致的。通过式(10)~式(12)计算得到细沟侵蚀后地表粗糙度、地形起伏度和地表切割深度的变化范围为0.33~2.35、0.47~4.35和0.53~2.53 cm(表 2)。在同一坡度下,地表粗糙度、地形起伏度和地表切割深度总体上均随流量增大而增大。在同一流量下,地表粗糙度和地表切割深度随坡度增大呈先增后减的趋势,在15°时减小,坡度升至20°时增大;小流量(2、4 L·min–1)时地形起伏度在15°时达到最大值后减小,而大流量(8、16 L·min–1)时在15°时有所减小,坡度升至20°时增大。
|
|
表 2 不同水力工况下侵蚀后微地形因子变化特征值 Table 2 Characteristic values of micro-topographic factors after scouring under different hydraulic conditions |
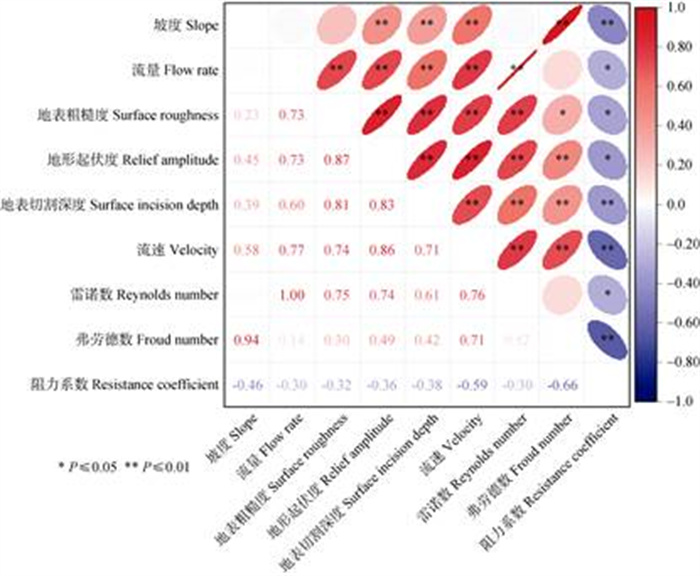
为明确水力工况条件及微地形因子与水力学特征参数间的关系,进行了相关性分析,结果如图 6所示。地表粗糙度与流量、流速和雷诺数呈极显著正相关(P < 0.01),相关系数均大于0.70,地形起伏度和地表切割深度与坡度、流量、流速、雷诺数和弗劳德数呈极显著正相关(P < 0.01);地表切割深度、地表粗糙度、地形起伏度与阻力系数呈极显著或显著负相关(P < 0.05)。
|
图 6 微地形因子与水力学特征参数的相关关系 Fig. 6 Correlation between micro-topographic factors and hydraulic parameters |
由于地表粗糙度、地形起伏度、地表切割深度与流速、雷诺数显示了较其他水力学参数更强的相关性,因此,本文重点探讨3个微地形因子与流速、雷诺数的响应关系。如表 3显示,饱和坡面侵蚀后的地表粗糙度、地形起伏度和地表切割深度与流速的关系可以用线性函数较好地描述,除5°时地表粗糙度和流速的拟合决定系数R2小于0.60外,其余模型的决定系数R2均大于0.92,且P < 0.01。3个微地形因子则与雷诺数整体上呈现良好的幂函数关系,大多数坡度下的拟合系数R2均大于0.61,P < 0.01。
|
|
表 3 微地形因子与流速、雷诺数的拟合关系 Table 3 Fitting the relationship of microtopographic factors with flow velocity and Reynolds number |
流速受到坡度、流量、下垫面条件等多种因素影响。从图 2和图 3可知,坡度和流量对饱和黄绵土坡面细沟水流流速有显著影响(P < 0.05)。但Nearing等[22]的研究表明流速与坡度无关,只与流量存在函数关系。这与本试验研究结果不同,可能的原因是试验所设计的坡度范围不同,他们的试验设计是缓坡条件(2°~10°),水流能量较低,导致流速对坡度变化不敏感。本研究中,图 3表示流速与坡度和流量的关系可用幂函数较好地描述,同时坡度和流量的幂指数分别为0.41和0.37,表明流速随坡度和流量的增大而增大,且与流量相比,坡度对流速的影响更大。这一结果与杨大明等[23]通过放水冲刷试验测定黄绵土坡面细沟流速的研究结果一致。随流量增加,水流具有的原始动能增大;当坡度增加时,单位水体的重力势能增加,水流重力沿坡面的分力增大,冲刷过程中消耗水流动能减小,从而导致流速增加[24]。Huang等[17]通过室内模拟土槽试验,研究了不同坡度和流量条件下饱和黄绵土坡面初始态与稳定态的细沟水流流速,研究结果同样表明流速随坡度和流量的增大而增大,且坡度对流速的影响大于流量。因此,当研究范围拓展至陡坡时,应考虑坡度和流量对流速的共同影响。综上,细沟水流流速受坡度和流量共同影响,随坡度和流量增大而增大,且坡度对流速的影响程度大于流量。
同时,研究结果显示地表粗糙度、地形起伏度和地表切割深度与坡度、流量存在极显著正相关(P < 0.01),这一结果与钱秋颖[25]针对裸露砒砂岩区典型黄土坡面,通过监测自然降雨和放水冲刷试验探究水力侵蚀对微地形因子变化的研究结果类似。集中水流流量增大,流速增大,从而增强径流能量,使得细沟侵蚀作用强烈,搬运泥沙的能力也越强,导致地表微地形变化剧烈[26]。此外,坡度增加,径流流速和剪切力也增大,下切侵蚀速率加快,同时,降低了沟壁的稳定性,加剧了对坡面完整度的破坏,导致地表微地形起伏增大[27-28]。而当坡度达到15°时,细沟中由于坍塌作用,水流中存在大量泥沙,降低水流对坡面土壤的直接剪切作用力[29],导致地表粗糙度、地形起伏度和切割深度减小,坡度继续增大至20°时,水流速度增大,侵蚀作用增强,重新塑造细沟形态,侵蚀后的微地形因子又增大。上述表明坡度和流量对细沟侵蚀后的微地形塑造起着重要作用,微地形因子随着坡度和流量的增大而增大,标志着坡面微地形向着利于侵蚀发生的方向进行。
3.2 微地形因子变化对水力学参数特征的响应水力学特征参数随侵蚀持续发生变化,同时直接影响侵蚀阶段微地形的演变。本研究表明,地表粗糙度、地形起伏度和地表切割深度与流速呈极显著正相关(r≥0.71,P < 0.01),且表 3显示微地形因子变化与流速之间的关系可以用线性函数较好拟合,这表明随流速增大,地表粗糙度、地形起伏度和地表切割深度均呈现增加趋势。坡面土壤侵蚀的主要动力来源于水流的拖曳力,而坡面水流流速是决定拖曳力大小的主导因素,细沟侵蚀导致的地表高差变化决定了微地形的变化,径流流速越快,侵蚀能力越强,坡面地表的高差越大,微地形因子均增大[26]。同时,地表粗糙度、地形起伏度和地表切割深度与雷诺数也呈极显著正相关(r≥0.61,P < 0.01),流量从2 L·min–1增大至4 L·min–1,细沟水流形态从层流转变为过渡流,此时地表粗糙度、地形起伏度和地表切割深度相对增幅分别为116%、60%和53%。增大至8 L·min–1时,这3个微地形因子相对增幅为147%、141%和105%。流量为16 L·min–1时,细沟水流为紊流,此时这3个微地形因子相对增幅分别为228%、231%和133%。可以看出,随流量增大,水流形态发生了显著变化,从层流逐渐转变过渡流和紊流过程中,侵蚀重塑后的微地形因子变幅均增大。且小流量时地表粗糙度变幅最大,随着流量增大,地表起伏度和地表切割深度变幅逐渐增大,表明水流对坡面细沟下切作用增强。流量增大引起雷诺数增大,导致水流的紊动程度增大,径流不断扰动地表,对坡面冲刷能力增强,侵蚀过程中不断加深细沟深度,地形起伏和地表切割深度增大[30]。本研究中3个微地形因子对雷诺数的变化表现出的响应关系符合幂函数。雷诺数越大,细沟水流的紊动程度增大,地表微地形因子对雷诺数的响应增强[31]。但3个微地形因子对流速和雷诺数的响应强度在15°时有所减弱,分析其原因是在15°时细沟以下切侵蚀为主,侵蚀过程中发生沟壁坍塌现象,泥沙堆积使坡面形态多变,造成了地形因子均有所减小,导致微地形因子与流速和雷诺数的响应关系减弱。而当坡度增大至20°时,沿坡面的重力分力增大,水流速度更快,雷诺数也增大,此时下切侵蚀作用更加强烈,导致地表粗糙度、地形起伏度和地表切割深度增大[27],因此微地形因子对流速和雷诺数的响应程度增强。综上所述,随细沟侵蚀的持续,水流水力学特征参数(流速和雷诺数)的变化加剧了地表微地形的起伏,地表粗糙度、地形起伏度和地表切割深度对流速和雷诺数变化的响应遵循线性和幂函数关系,小流量时地表粗糙度变幅最大,随着流量增大,地表起伏度和地表切割深度变幅逐渐增大,表明水流对坡面细沟下切作用增强。
4 结论本研究通过对饱和黄绵土进行冲刷试验发现,随着坡度和流量增加,水流速度明显增大,且流速与坡度、流量呈幂函数关系,坡度较流量对流速的影响更大;水流状态从层流逐渐转变过渡流和紊流,且所有处理下均处于急流范畴,阻力系数随坡度和流量的变化无明显规律。随着坡度和流量的增大地表微地形因子均有不同程度的增大,标志着坡面微地形向着有利于侵蚀发生的方向进行。水流的水力学特征参数(如流速、雷诺数)对地表微地形变化具有显著影响,小流量时地表粗糙度变幅最大,随着流量增大,地表起伏度和地表切割深度变幅逐渐增大,表明侵蚀过程中径流下切作用强烈,细沟侵蚀深度不断增大。研究结果可为黄绵土坡耕地水土流失治理工作以及区域生态修复研究提供理论基础。
| [1] |
Omidvar E, Hajizadeh Z, Ghasemieh H. Sediment yield, runoff and hydraulic characteristics in straw and rock fragment covers[J]. Soil and Tillage Research, 2019, 194: 104324. DOI:10.1016/j.still.2019.104324
(  0) 0) |
| [2] |
Li D D, Chen X Y, Han Z, et al. Determination of rill erodibility and critical shear stress of saturated purple soil slopes[J]. International Soil and Water Conservation Research, 2022, 10(1): 38-45. DOI:10.1016/j.iswcr.2021.04.013
(  0) 0) |
| [3] |
Rahma A E, Warrington D N, Lei T W. Efficiency of wheat straw mulching in reducing soil and water losses from three typical soils of the Loess Plateau, China[J]. International Soil and Water Conservation Research, 2019, 7(4): 335-345. DOI:10.1016/j.iswcr.2019.08.003
(  0) 0) |
| [4] |
Han Z, Chen X Y, Li Y H, et al. Estimating rill erosion and sediment transport processes along a saturated purple soil slope[J]. Canadian Journal of Soil Science, 2021, 101(3): 507-516. DOI:10.1139/cjss-2020-0119
(  0) 0) |
| [5] |
Jiang Y M, Shi H J, Wen Z M, et al. The dynamic process of slope rill erosion analyzed with a digital close range photogrammetry observation system under laboratory conditions[J]. Geomorphology, 2020, 350: 106893. DOI:10.1016/j.geomorph.2019.106893
(  0) 0) |
| [6] |
Zhang G H, Xie Z F. Soil surface roughness decay under different topographic conditions[J]. Soil and Tillage Research, 2019, 187: 92-101. DOI:10.1016/j.still.2018.12.003
(  0) 0) |
| [7] |
Kuhn N J, van Oost K, Cammeraat E. Soil erosion, sedimentation and the carbon cycle[J]. Catena, 2012, 94: 1-2. DOI:10.1016/j.catena.2011.11.007
(  0) 0) |
| [8] |
Rao W L, Zhang Q F, Qian Z Y, et al. Microtopographic response of tilled loess slopes during stages of water erosion development[J]. Catena, 2024, 245: 108309. DOI:10.1016/j.catena.2024.108309
(  0) 0) |
| [9] |
Wang R, Li P, Li Z B, et al. Effects of gully head height and soil texture on gully headcut erosion in the Loess Plateau of China[J]. Catena, 2021, 207: 105674. DOI:10.1016/j.catena.2021.105674
(  0) 0) |
| [10] |
Li L, Qin F C, Qian Q Y, et al. Micro-geomorphic change characteristics and process of slope under water erosion in pisha sandstone area (In Chinese)[J]. Soils, 2022, 54(1): 198-205. [李龙, 秦富仓, 钱秋颖, 等. 砒砂岩区水力侵蚀下坡面微地貌变化特征及过程研究[J]. 土壤, 2022, 54(1): 198-205.]
(  0) 0) |
| [11] |
Zhang Q F, Wang J, Wu F Q. Spatial heterogeneity of surface roughness on tilled loess slopes in erosion stages[J]. Soil and Water Research, 2018, 13(2): 90-97. DOI:10.17221/130/2017-SWR
(  0) 0) |
| [12] |
Liang X L, Zhao L S, Wu J, et al. Simulation of response law for soil surface roughness and hydraulics parameters of runoff (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(19): 123-131. DOI:10.3969/j.issn.1002-6819.2014.19.015 [梁心蓝, 赵龙山, 吴佳, 等. 地表糙度与径流水力学参数响应规律模拟[J]. 农业工程学报, 2014, 30(19): 123-131.]
(  0) 0) |
| [13] |
Bertolino A V F A, Fernandes N F, Miranda J P L, et al. Effects of plough pan development on surface hydrology and on soil physical properties in Southeastern Brazilian plateau[J]. Journal of Hydrology, 2010, 393(1/2): 94-104.
(  0) 0) |
| [14] |
Rahma A E, Wang W, Tang Z J, et al. Straw mulch can induce greater soil losses from loess slopes than no mulch under extreme rainfall conditions[J]. Agricultural and Forest Meteorology, 2017, 232: 141-151. DOI:10.1016/j.agrformet.2016.07.015
(  0) 0) |
| [15] |
Wang W, Chen Y, Zhuang X H, et al. Spatial distribution of overland flow velocity along straw-mulched slope under extreme rainfall (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2022, 38(2): 149-156. [王伟, 陈杨, 庄晓晖, 等. 极端降雨条件下秸秆覆盖坡面水流流速空间分布[J]. 农业工程学报, 2022, 38(2): 149-156.]
(  0) 0) |
| [16] |
Guan Y B, Yang S T, Zhao C S, et al. Monitoring long-term gully erosion and topographic thresholds in the marginal zone of the Chinese Loess Plateau[J]. Soil and Tillage Research, 2021, 205: 104800. DOI:10.1016/j.still.2020.104800
(  0) 0) |
| [17] |
Huang Y H, Chen X Y, Li F H, et al. Velocity of water flow along saturated loess slopes under erosion effects[J]. Journal of Hydrology, 2018, 561: 304-311. DOI:10.1016/j.jhydrol.2018.03.070
(  0) 0) |
| [18] |
Wang R, Li P, Han J C, et al. Effects of gully head height and soil texture on headward erosion characteristics and topography evolution (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2021, 37(10): 91-99. DOI:10.11975/j.issn.1002-6819.2021.10.011 [王睿, 李鹏, 韩建纯, 等. 沟头高度和土壤质地对细沟溯源侵蚀特征和形态发育的影响[J]. 农业工程学报, 2021, 37(10): 91-99.]
(  0) 0) |
| [19] |
Zhuang X H, Wang W, Ma Y Y, et al. Spatial distribution of sheet flow velocity along slope under simulated rainfall conditions[J]. Geoderma, 2018, 321: 1-7. DOI:10.1016/j.geoderma.2018.01.036
(  0) 0) |
| [20] |
Gao X F, Shi X N, Lei T W, et al. An experimental investigation of the effects of thawed soil depth on rill flow velocity[J]. Hydrological Processes, 2021, 35(2): e14043. DOI:10.1002/hyp.14043
(  0) 0) |
| [21] |
Tan W H, Chen X Y, Tao T T, et al. Experiment study of sheet and rill flow hydraulic characteristics and the critical conditions on saturated purple soil slopes in Chongqing (In Chinese)[J]. Journal of Soil and Water Conservation, 2023, 37(3): 66-72. [谭文浩, 陈晓燕, 陶婷婷, 等. 重庆饱和紫色土坡面片流与细沟流水力学特性及临界条件试验研究[J]. 水土保持学报, 2023, 37(3): 66-72.]
(  0) 0) |
| [22] |
Nearing M A, Polyakov V O, Nichols M H, et al. Slope–velocity equilibrium and evolution of surface roughness on a stony hillslope[J]. Hydrology and Earth System Sciences, 2017, 21(6): 3221-3229. DOI:10.5194/hess-21-3221-2017
(  0) 0) |
| [23] |
Yang D M, Gao P L, Liu X Y, et al. Hydraulic characteristics of slope land under rill erosion (In Chinese)[J]. Journal of Hydroelectric Engineering, 2017, 36(10): 65-73. [杨大明, 高佩玲, 刘小媛, 等. 细沟侵蚀下的坡面水动力学特性研究[J]. 水力发电学报, 2017, 36(10): 65-73.]
(  0) 0) |
| [24] |
Ban Y Y, Lei T W, Liu Z Q, et al. Comparison of rill flow velocity over frozen and thawed slopes with electrolyte tracer method[J]. Journal of Hydrology, 2016, 534: 630-637. DOI:10.1016/j.jhydrol.2016.01.028
(  0) 0) |
| [25] |
Qian Q Y. Study on the influence of water erosion on the micro-topography of the slope in the bare arsenic sandstone area[D]. Inner Mongolia: Inner Mongolia Agricultyural University, 2021.[钱秋颖. 水力侵蚀对裸露砒砂岩区坡面微地形的影响研究[D]. 内蒙古: 内蒙古农业大学, 2021.]
(  0) 0) |
| [26] |
Ma M J, Wang J G, Guo Z L, et al. Research on sediment and solute transport on red soil slope under simultaneous influence of scouring flow (In Chinese)[J]. Acta Pedologica Sinica, 2016, 53(2): 365-374. [马美景, 王军光, 郭忠录, 等. 放水冲刷对红壤坡面侵蚀过程及溶质迁移特征的影响[J]. 土壤学报, 2016, 53(2): 365-374.]
(  0) 0) |
| [27] |
Li L, Nearing M A, Polyakov V O, et al. Evolution of rock cover, surface roughness, and its effect on soil erosion under simulated rainfall[J]. Geoderma, 2020, 379: 114622. DOI:10.1016/j.geoderma.2020.114622
(  0) 0) |
| [28] |
Yang F X, Zheng Z C, Li T X, et al. Variation characteristics of slope surface microtopography and its response to seepage under different artificial management measures (In Chinese)[J]. Journal of Soil and Water Conservation, 2023, 37(3): 73-80. [杨斐雄, 郑子成, 李廷轩, 等. 不同人为管理措施坡面地表微地形变化特征及其对渗流的响应[J]. 水土保持学报, 2023, 37(3): 73-80.]
(  0) 0) |
| [29] |
Xiao H, Liu G, Liu P L. Response of detachment rate of loess slope to hydrodynamic characteristics under concentrate flow condition (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(17): 106-111. [肖海, 刘刚, 刘普灵. 集中流作用下黄土坡面剥蚀率对侵蚀动力学参数的响应[J]. 农业工程学报, 2016, 32(17): 106-111.]
(  0) 0) |
| [30] |
Tao T T, Chen X Y, Chen S Q, et al. Hydraulic characteristics of rills of non-eroded and eroding on saturated purple soil (In Chinese)[J]. Acta Pedologica Sinica, 2022, 59(1): 129-138. [陶婷婷, 陈晓燕, 陈仕奇, 等. 饱和紫色土初始态和稳定态细沟水力学特征研究[J]. 土壤学报, 2022, 59(1): 129-138.]
(  0) 0) |
| [31] |
Nicosia A, Di Stefano C, Palmeri V, et al. Flow resistance of overland flow on a smooth bed under simulated rainfall[J]. Catena, 2020, 187: 104351.
(  0) 0) |
 2025, Vol. 62
2025, Vol. 62


