非饱和土壤水流动是指土壤中水分未充满全部孔隙时的水分运移^[1]。降雨时水向土中入渗及对地下水的补给、田间滴灌条件下土壤水分运移等均可简化为非饱和土壤水的一维流动^[2-3]。

人们对非饱和土壤水流动的研究有较长历史，其科学理论形成始于1856年法国工程师达西进行的水分渗透试验^[4]。理查兹于1931年在达西定律和质量守恒原理基础上推导出描述非饱和土壤水流动数学模型——理查兹方程^[5]。求解理查兹方程需要两个本构关系，即土壤水分特征曲线和土壤导水率曲线，但理查兹未给出这两个本构关系的函数关系式。因此，研究人员后续重点研究这两个本构关系^[6]。目前广泛使用的本构关系由Mualem^[7]和van Genuchten^[8]于1976年和1980年提出。理查兹^[9-10]方程存在非线性、高阶偏微分等特征，这给非饱和土壤水运动的定量研究带来了许多挑战。随着计算机技术的发展，有限元数值模拟成为解决土壤水分运移问题的主流方法。例如，目前广泛使用的商业模型HYDRUS就是基于有限元法求解理查兹方程。

《新时代中国土壤物理学主要领域进展与展望》一文^[11]指出“我国土壤物理学虽然发展迅速，队伍不断壮大，在国际上影响力不断提升，但是科研主要集中在少数单位，发展非常不平衡，原创性研究较少，在国际上领先的研究则更加凤毛麟角”。

以有限元法求解理查兹方程为例，现有的学习材料主要是相关的中文^[12-14]和英文学术论文^[15]、教科书^[16]和商业模型HYDRUS用户手册^[17]。上述材料理论性偏强，缺乏针对数理基础薄弱读者的详细解释和逐步引导，导致学习难度大，编程则更是难以开展且消耗精力。

不但土壤物理领域的研究人员有上述困境，其他领域的研究人员也有类似困扰。化工领域的毕超^[18]针对这一问题撰写了《计算流体力学有限元方法及其编程详解》一书。该书的写作模式是十分适用于数理基础不强读者入门计算流体力学的有限元法。有限元法求解理查兹方程的本质是用该方法求解流体力学问题。该书给出了不少流体力学案例的编程思路和代码，但是没有给出理查兹方程求解的具体案例。

因此，本文依照此书的写作模式，提供了详细的可操作性强的有限元法求解理查兹方程的编程思路及相应代码。能够让有需要的相关研究人员较快入门非饱和土壤水一维流动有限元法求解，为后续解决更为复杂的土壤物理数值模拟问题奠定基础。针对彭新华等^[11]提出的我国在土壤物理过程数值模拟上实现突破存在一定难度的问题起到一些积极的作用。

1 一维理查兹方程

一维理查兹方程以体积含水量$\theta $ [L³L^–3]为因变量的公式为：

$ \frac{{\partial \theta }}{{\partial t}} + \frac{\partial }{{\partial z}}\left[ {K\left( \theta \right) - D\left( \theta \right)\frac{{\partial \theta }}{{\partial z}}} \right] = 0 $

(1)

式中，t[T]为时间，$z$[L]为土壤深度，$K\left( \theta \right)$ [LT^–1]为非饱和土壤导水率，$D\left( \theta \right)$ [L²T^–1]为土壤水扩散率。

本文采用Celia等^[10]文中的土壤入渗试验参数：

初始条件为：

$ t=0, \quad \theta_0=0.1099=0.1099 $

(2a)

上边界条件为：

$ {\theta _1}=0.2003 $

(2b)

下边界条件为：

$ {\theta _2}=0.1009 $

(2c)

Celia等^[10]文中给出的基于Mualem-van Genuchten模型^[7-8]的土壤水分特征曲线和土壤导水率曲线为：

$ \theta \left( h \right) = \frac{{{\theta _s} - {\theta _r}}}{{{{\left[ {1 + {{\left( {\alpha \left| h \right|} \right)}^n}} \right]}^m}}} + {\theta _r} $

(3)

$ K\left( h \right) = {k_s}\frac{{{{\left\{ {1 - {{\left( {\alpha \left| h \right|} \right)}^{n - 1}}\cdot{{\left[ {1 + {{\left( {\alpha \left| h \right|} \right)}^n}} \right]}^{ - m}}} \right\}}^2}}}{{{{\left[ {1 + {{\left( {\alpha \left| h \right|} \right)}^n}} \right]}^{m/2}}}} $

(4)

式中，h[L]为土壤基质势，θ_s[L³L^–3]为饱和土壤含水率，θ_r[L³L^–3]为滞留土壤残余含水率，α[L^–1]为与进气吸力有关的参数，n为形状系数，其中m=1–1/n，k_s[LT^–1]为土壤饱和导水率。上述各参数值列于表 1。

由式（3）得：

$ \left| h \right| = \frac{1}{\alpha }{\left[ {{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{1/m}} - 1} \right]^{1/n}} $

(5)

将式（5）代入式（4），得：

$ K\left( \theta \right) = {k_s}\frac{{{{\left\{ {1 - {{\left[ {{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{1/m}} - 1} \right]}^{\left( {n - 1} \right)/n}} \cdot {{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{ - 1}}} \right\}}^2}}}{{{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{1/2}}}} $

(6)

对式（3）求导，得：

$ \frac{{d\theta }}{{dh}} = \frac{{\left( {{\theta _s} - {\theta _r}} \right)\left( { - m} \right)n\alpha {{\left[ {{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{1/m}} - 1} \right]}^{\left( {n - 1} \right)/n}}}}{{{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{\left( {m + 1} \right)/m}}}} $

(7)

式（7）为比水容重，记为$C\left( \theta \right)$，代入土壤水扩散率公式$D\left( \theta \right) = K\left( \theta \right)/C\left( \theta \right)$，得：

$ D\left( \theta \right) = {k_s}\frac{{{{\left\{ {1 - {{\left[ {{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{1/m}} - 1} \right]}^{\left( {n - 1} \right)/n}} \cdot {{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{ - 1}}} \right\}}^2}\cdot{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{\left( {m + 1} \right)/m}}}}{{{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{1/2}}\cdot\left( {{\theta _s} - {\theta _r}} \right)\left( { - m} \right)n\alpha {{\left[ {{{\left( {\frac{{{\theta _s} - {\theta _r}}}{{\theta - {\theta _r}}}} \right)}^{1/m}} - 1} \right]}^{\left( {n - 1} \right)/n}}}} $

(8)

由此可知式（1）中非饱和土壤导水率和土壤水扩散率表达式。

2 一维理查兹方程有限元法求解编程思路 2.1 计算区域的离散

首先对一维理查兹方程的计算区域进行离散，相关内容详见毕超一书^[18]。

2.2 插值函数和权函数

采用高斯积分法计算积分，积分区域为[–1，1]，单元的坐标轴记为$\xi $，坐标轴原点为0点。一维理查兹方程在离散后的每一个单元上对应的插值函数ϕ$ (\xi )$为：

$ \mathit ф={\left({\mathit ф}_{1} {\mathit ф}_{2} {\mathit ф}_{3}\right)}^{T} $

(9)

单元内任意函数在原来的坐标轴z轴上可用二次多项式近似：

$ \theta \left( z \right) = C_1^e + C_2^ez + C_3^e{z^2} $

(10)

式中，$C_1^e$、$C_2^e$和$C_3^e$为待定系数，可由单元上的三个节点坐标及其对应的函数值$\left( {z_{\text{a}}^e,\theta _1^e} \right)$、$\left( {\frac{{z_a^e + z_b^e}}{2},\theta _2^e} \right)$和$\left( {z_{\text{b}}^e,\theta _3^e} \right)$代入式（10）求得。将求得的$C_1^e$、$C_2^e$和$C_3^e$再代入式（10），经过变换可得单元内任意一点函数值的表达式：

$ \theta ={\mathit ф}_{1}{\theta }_{1}^{e}+{\mathit ф}_{2}{\theta }_{2}^{e}+{\mathit ф}_{3}{\theta }_{3}^{e}={\mathit ф}^{T}{\theta }_{I}^{e} $

(11)

式中，$ {\mathit ф}_{1} $、$ {\mathit ф}_{2} $和$ {\mathit ф}_{3} $的表达式为：

$ {\mathit ф}_{1}=\frac{\left[\left({z}_{b}^{e}-{z}_{a}^{e}\right)-\left(z-{z}_{a}^{e}\right)\right]}{\left({z}_{b}^{e}-{z}_{a}^{e}\right)}\frac{\left[\left({z}_{b}^{e}-{z}_{a}^{e}\right)-2\left(z-{z}_{a}^{e}\right)\right]}{\left({z}_{b}^{e}-{z}_{a}^{e}\right)} $

(12a)

$ {\mathit ф}_{2}=4\frac{\left(z-{z}_{a}^{e}\right)\left[{z}_{b}^{e}-{z}_{a}^{e}-\left(z-{z}_{a}^{e}\right)\right]}{{\left({z}_{b}^{e}-{z}_{a}^{e}\right)}^{2}} $

(12b)

$ {\mathit ф}_{3}=\frac{\left(z-{z}_{a}^{e}\right)}{\left({z}_{b}^{e}-{z}_{a}^{e}\right)}\frac{\left[2\left(z-{z}_{a}^{e}\right)-\left({z}_{b}^{e}-{z}_{a}^{e}\right)\right]}{\left({z}_{b}^{e}-{z}_{a}^{e}\right)} $

(12c)

利用坐标轴变换等比关系：

$ \frac{{z - z_a^e}}{{z_b^e - z_a^e}} = \frac{{\xi - \left( { - 1} \right)}}{{1 - \left( { - 1} \right)}} = \frac{{\xi + 1}}{2} $

(13)

式（12）中$ {\mathit ф}_{1} $、$ {\mathit ф}_{2} $、$ {\mathit ф}_{3} $可转为：

$ {\mathit ф}_{1}=\frac{1}{2}\xi \left(\xi -1\right) $

(14a)

$ {\mathit ф}_{2}=\left(1-\xi \right)\left(1+\xi \right) $

(14b)

$ {\mathit ф}_{3}=\frac{1}{2}\xi \left(\xi +1\right) $

(14c)

插值函数对坐标$\xi $的导数为：

$ \frac{\partial {\mathit ф}_{1}}{\partial \xi }=\xi -\frac{1}{2} $

(15a)

$ \frac{\partial {\mathit ф}_{2}}{\partial \xi }=-2\xi $

(15b)

$ \frac{\partial {\mathit ф}_{3}}{\partial \xi }=\xi +\frac{1}{2} $

(15c)

2.3 加权余量方程的建立

伽辽金有限元方法中权函数等于插值函数。权函数与式（1）相乘，并在任一定义域[a，b]内积分，得：

$ \underset{a}{\overset{b}{{\displaystyle \int }}}\mathit ф\left\{\frac{\partial \theta }{\partial t}+\frac{\partial }{\partial z}\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]\right\}dz=0 $

(16)

式（16）简化得：

$ \underset{a}{\overset{b}{{\displaystyle \int }}}\mathit ф\frac{\partial \theta }{\partial t}dz+\underset{a}{\overset{b}{{\displaystyle \int }}}\mathit ф\frac{\partial }{\partial z}\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]dz=0 $

(17)

采用分部积分法对式（17）中第二部分作如下变换：

$ \begin{array}{l}\underset{a}{\overset{b}{{\displaystyle \int }}}\mathit ф\frac{\partial }{\partial z}\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]dz\\ ={\left\{\mathit ф\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]\right\}}_{a}^{b}-\underset{a}{\overset{b}{{\displaystyle \int }}}\frac{d\mathit ф}{dz}\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]dz\end{array} $

(18)

将式（18）代入式（17），得：

$ \underset{a}{\overset{b}{{\displaystyle \int }}}\mathit ф\frac{\partial \theta }{\partial t}dz+{\left\{\mathit ф\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]\right\}}_{a}^{b}-\underset{a}{\overset{b}{{\displaystyle \int }}}\frac{d\mathit ф}{dz}\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]dz=0 $

(19)

由于Celia等^[10]文中使用的上、下边界条件为第一类边界条件，即$ {\left\{\mathit ф\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]\right\}}_{a}^{b}=0 $，则

式（19）可简化为：

$ \underset{a}{\overset{b}{{\displaystyle \int }}}\mathit ф\frac{\partial \theta }{\partial t}dz-\underset{a}{\overset{b}{{\displaystyle \int }}}\frac{d\mathit ф}{dz}\left[K\left(\theta \right)-D\left(\theta \right)\frac{\partial \theta }{\partial z}\right]dz=0 $

(20)

2.4 单元有限元方程的建立

建立单元方程时，需将式（20）的积分区域变换为单元区域。将式（11）代入式（20），得：

$ \underset{{z}_{1}^{e}}{\overset{{z}_{2}^{e}}{{\displaystyle \int }}}\mathit ф\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}}{\partial t}dz-\underset{{z}_{1}^{e}}{\overset{{z}_{2}^{e}}{{\displaystyle \int }}}\frac{d\mathit ф}{dz}\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}}{\partial z}\right]dz=0 $

(21)

式（21）简化得：

$ \frac{\partial {\theta }_{I}^{e}}{\partial t}\underset{{z}_{1}^{e}}{\overset{{z}_{2}^{e}}{{\displaystyle \int }}}\mathit ф{\mathit ф}^{T}dz-\underset{{z}_{1}^{e}}{\overset{{z}_{2}^{e}}{{\displaystyle \int }}}\frac{d\mathit ф}{dz}\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}}{\partial z}\right]dz=0 $

(22)

采用后向差分法对式（22）中$\frac{{\partial \theta _I^e}}{{\partial t}}$进行处理，得：

$ \frac{{\partial \theta _I^e}}{{\partial t}} = \frac{{\theta {{_I^e}^{\left( i \right)}} - \theta {{_I^e}^{\left( {i - 1} \right)}}}}{{\Delta t}} $

(23)

式（23）中$ \theta_I^{e(i)}$为当前时刻值，$ \theta_I^{e(i-1)}$为前一时刻值。

将式（23）代入式（22），得：

$ \frac{{\theta }_{I}^{e}{}^{\left(i\right)}-{\theta }_{I}^{e}{}^{\left(i-1\right)}}{\Delta t}\underset{{z}_{1}^{e}}{\overset{{z}_{2}^{e}}{{\displaystyle \int }}}\mathit ф{\mathit ф}^{T}dz-\underset{{z}_{1}^{e}}{\overset{{z}_{2}^{e}}{{\displaystyle \int }}}\frac{d\mathit ф}{dz}\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}}{\partial z}\right]dz=0 $

(24)

采用高斯数值积分法求解式（24）中的积分项。利用雅可比矩阵可将坐标z变换到坐标$\xi $：

$ \mathop \smallint \limits_{z_1^e}^{z_2^e} G\left( z \right)dz = \mathop \smallint \limits_{ - 1}^1 {G^*}\left( \xi \right)\left| J \right|d\xi $

(25)

式（25）中$G\left( z \right)$为任意函数，$J$为雅可比矩阵，对于一维问题，其具体形式如下：

$ J = \frac{{\partial z}}{{\partial \xi }} $

(26)

根据导数关系：

$ \frac{d\mathit ф}{dz}=\frac{d\mathit ф}{d\xi }\frac{d\xi }{dz}=\frac{d\mathit ф}{d\xi }{J}^{-1} $

(27)

对式（24）进行积分变换并将式（27）代入，得：

$ \begin{array}{l}\frac{{\theta }_{I}^{e}{}^{\left(i\right)}-{\theta }_{I}^{e}{}^{\left(i-1\right)}}{\Delta t}\underset{-1}{\overset{1}{{\displaystyle \int }}}\mathit ф{\mathit ф}^{T}\left|J\right|d\xi -\underset{-1}{\overset{1}{{\displaystyle \int }}}\frac{d\mathit ф}{d\xi }{J}^{-1}\\ ·\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}}{\partial \xi }{J}^{-1}\right]\left|J\right|d\xi =0\end{array} $

(28)

利用高斯数值积分公式，式（28）可变换为：

$ \begin{array}{l}\frac{{\theta }_{I}^{e}{}^{\left(i\right)}-{\theta }_{I}^{e}{}^{\left(i-1\right)}}{\Delta t}\displaystyle \sum\limits _{i=1}^{6}{\omega }_{i}\mathit ф{\mathit ф}^{T}\left|J\right|-\displaystyle \sum\limits_{i=1}^{6}{\omega }_{i}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1}\\ ·\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}}{\partial {\xi }_{i}}{J}^{-1}\right]\left|J\right|=0\end{array} $

(29)

式中，${\omega _i}$为积分权，${\xi _i}$为积分点。

式（29）中$ \displaystyle \sum\limits _{i=1}^{6}{\omega }_{i}\mathit ф{\mathit ф}^{T}\left|J\right| $为质量矩阵，记为M，则式（29）简化为：

$ \begin{array}{l}M{\theta }_{I}^{e}{}^{\left(i\right)}-M{\theta }_{I}^{e}{}^{\left(i-1\right)}-\Delta t \displaystyle \sum\limits _{i=1}^{6}{\omega }_{i}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1}\\ ·\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}}{\partial {\xi }_{i}}{J}^{-1}\right]\left|J\right|=0\end{array} $

(30)

2.5 牛顿-拉夫逊法求解方程

式（30）为非线性代数式，故可利用牛顿-拉夫逊法求解。令式（30）等于$R\left( \theta \right)$，得：

$ \begin{array}{l}R\left(\theta \right)=M{\theta }_{I}^{e}{}^{\left(i\right)}-M{\theta }_{I}^{e}{}^{\left(i-1\right)}-\Delta t \displaystyle \sum \limits_{i=1}^{6}{\omega }_{i}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1}\\ ·\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}}{\partial {\xi }_{i}}{J}^{-1}\right]\left|J\right|=0\end{array} $

(31)

对式（31）中的当前时刻值求导，得：

$ R\text{'}\left(\theta \right)=M-\Delta t\displaystyle \sum\limits_{i=1}^{6}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1}{\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}}{\partial {\xi }_{i}}{J}^{-1}\right]}^{\text{'}}\left|J\right| $

(32)

为利于表示，令$ {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}={\theta }_{i} $，得：

$ R\text{'}\left(\theta \right)=M-\Delta t\displaystyle \sum\limits_{i=1}^{6}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1}{\left[K\left({\theta }_{i}\right)-D\left({\theta }_{i}\right){J}^{-1}\frac{\partial {\theta }_{i}}{\partial {\xi }_{i}}\right]}^{\text{'}}\left|J\right| $

(33)

令式（33）中的$K\left( {{\theta _i}} \right) - D\left( {{\theta _i}} \right){J^{ - 1}}\frac{{\partial {\theta _i}}}{{\partial {\xi _i}}} = {j_k}$，${J^{ - 1}}\frac{{\partial {\theta _i}}}{{\partial {\xi _i}}} = {g_k}$，得：

$ {j_k}\left( {{\theta _i},{g_k}} \right) = K\left( {{\theta _i}} \right) - D\left( {{\theta _i}} \right){g_k} $

(34)

利用全微分法对式（34）求导，得：

$ \begin{gathered} d{j_k} = \frac{{\partial {j_k}}}{{\partial {\theta _i}}}d{\theta _i} + \frac{{\partial {j_k}}}{{\partial {g_k}}}d{g_k} = \left[ {K'\left( {{\theta _i}} \right) - {g_k} \cdot D{\text{'}}\left( {{\theta _i}} \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d{\theta _i} - D\left( {{\theta _i}} \right)d{g_k} \hfill \\ \end{gathered} $

(35)

将式（35）代入式（33），得：

$ R\text{'}\left(\theta \right)=M-nt \displaystyle \sum\limits_{i=1}^{6}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1}\left\{\left[K\text{'}\left({\theta }_{i}\right)-{g}_{k}D\text{'}\left({\theta }_{i}\right)\right]d{\theta }_{i}-D\left({\theta }_{i}\right)d{g}_{k}\right\}\left|J\right| $

(36)

式中，$ d{\theta }_{i}={\mathit ф}^{T} $，$ d{g}_{k}=\frac{d{\mathit ф}^{T}}{d\xi }{J}^{-1} $。

令式（31）中$ \displaystyle \sum\limits_{i=1}^{6}{\omega }_{i}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1}\left[K\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)-D\left({\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}\right)\frac{\partial {\mathit ф}^{T}{\theta }_{I}^{e}{}^{\left(i\right)}}{\partial {\xi }_{i}}{J}^{-1}\right]\left|J\right|=F $，则式（31）可简化为：

$ R(\theta)=M \theta_I^{e(i)}-M \theta_I^{e(i-1)}-\Delta t \cdot F=0 $

(37)

令式（36）中$ \displaystyle \sum\limits_{i=1}^{6}\frac{d\mathit ф}{d{\xi }_{i}}{J}^{-1} $ $ \left\{ {\left[ {K'\left( {{\theta _i}} \right) - {g_k}D'\left( {{\theta _i}} \right)} \right]} \right. $ $ \left. {d{\theta _i} - D\left( {{\theta _i}} \right)d{g_k}} \right\}\left| J \right| = T $，则式（36）可简化为：

$ R'\left( \theta \right) = M - \Delta t \cdot T $

(38)

由牛顿-拉夫逊法可得：

$ \Delta \theta = - \frac{{R\left( \theta \right)}}{{R'\left( \theta \right)}} $

(39)

将$R\left( \theta \right)$和$R'\left( \theta \right)$代入式（39）并简化，得：

$ M \cdot \Delta \theta-\Delta t \cdot T \cdot \Delta \theta+M \theta_I^{e(i)}-M \theta_I^{e(i-1)}=\Delta t \cdot F $

(40)

2.6 总体方程的组合

上述方程的组合方法可详见毕超^[18]一书。

2.7 代入边界条件求解

组合后可得到一个矩阵形式的方程组，根据Reddy^[19]一书的方法代入第一类边界条件求解。为便于说明，以式（41）为例：

$ \left[ {\begin{array}{*{20}{c}} {{K_{11}}}&{{K_{12}}}&{{K_{13}}}&{{K_{14}}} \\ {{K_{21}}}&{{K_{22}}}&{{K_{23}}}&{{K_{24}}} \\ {{K_{31}}}&{{K_{32}}}&{{K_{33}}}&{{K_{34}}} \\ {{K_{41}}}&{{K_{42}}}&{{K_{43}}}&{{K_{44}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{U_1} = \Delta 1} \\ {{U_2}} \end{array}} \\ {{U_3}} \\ {{U_4} = \Delta 2} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{Q_1}} \\ {{Q_2}} \end{array}} \\ {{Q_3}} \\ {{Q_4}} \end{array}} \right\} $

(41)

式中，${U_1}$和${U_4}$的值分别为Δ1和Δ1，即代表两个端点已知的第一类边界条件。

由矩阵计算得：

$ {K_{11}}{U_1} + {K_{12}}{U_2} + {K_{13}}{U_3} + {K_{14}}{U_4} = {Q_1} $

(42a)

$ {K_{21}}{U_1} + {K_{22}}{U_2} + {K_{23}}{U_3} + {K_{24}}{U_4} = {Q_2} $

(42b)

$ {K_{31}}{U_1} + {K_{32}}{U_2} + {K_{33}}{U_3} + {K_{34}}{U_4} = {Q_3} $

(42c)

$ {K_{41}}{U_1} + {K_{42}}{U_2} + {K_{43}}{U_3} + {K_{44}}{U_4} = {Q_4} $

(42d)

未知的${U_2}$和${U_3}$只需两个方程即可求解，故舍去式（42a）与式（42d）。将式（42b）与式（42c）进一步拆分形成方阵，得：

$ \left[ {\begin{array}{*{20}{c}} {{K_{22}}}&{{K_{23}}} \\ {{K_{32}}}&{{K_{33}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{U_2}} \\ {{U_3}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{K_{21}}}&{{K_{24}}} \\ {{K_{31}}}&{{K_{34}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{U_1}} \\ {{U_4}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{Q_2}} \\ {{Q_3}} \end{array}} \right\} $

(43)

令p为已知节点，f为自由节点，即p=1，4，f=2，3。则式（43）可简化为：

$ K\left( {f,f} \right)\cdot U\left( {f,1} \right) + K\left( {f,p} \right) \cdot U\left( {p,1} \right) = Q\left( {f,1} \right) $

(44)

式（40）经过组合后的表达式为：

$ M\cdot\Delta \theta - \Delta t\cdot T\cdot\Delta \theta + M{\theta ^{\left( i \right)}} - M{\theta ^{\left( {i - 1} \right)}} = \Delta t\cdot F $

(45)

类似式（41）—式（44），式（45）同理可转换为：

$ \begin{aligned} & M(f, f) \Delta \theta(f, 1)+M(f, p) \Delta \theta(p, 1)-\Delta t[T(f, f) \Delta \theta(f, 1)+T(f, p) \Delta \theta(p, 1)] \\ & +M(f, f) \theta^{(i)}(f, 1)+M(f, p) \theta^{(i)}(p, 1) \\ & -\left[M(f, f) \theta^{(i-1)}(f, 1)+M(f, p) \theta^{(i-1)}(p, 1)\right]=\Delta t \cdot F(f, 1) \end{aligned} $

(46)

由于已知节点的数值是常数，则$\Delta \theta \left( {p,1} \right) = 0$，式（46）可简化为：

$ \begin{gathered} \left[ {{\text{M}}\left( {f,f} \right) - \Delta {\text{t}} \cdot {\text{T}}\left( {f,f} \right)} \right]\Delta {\text{θ }}\left( {f,1} \right) = \Delta {\text{t}} \cdot {\text{F}}\left( {f,1} \right) - {\text{M}}\left( {f,f} \right) \cdot \hfill \\ \left[ {{\theta ^{\left( i \right)}}\left( {f,1} \right) - {\theta ^{\left( {i - 1} \right)}}\left( {f,1} \right)} \right] - {\text{M}}\left( {f,p} \right)\left[ {{\theta ^{\left( i \right)}}\left( {p,1} \right) - {\theta ^{\left( {i - 1} \right)}}\left( {p,1} \right)} \right] \hfill \\ \end{gathered} $

(47)

经矩阵计算可得$ \Delta {\text{θ }}\left( {f,1} \right) $，继而由牛顿-拉夫逊法得：

$ {\theta ^{\left( {f,i} \right)}} = {\theta ^{\left( {f,i - 1} \right)}} + \Delta \theta \left( {f,1} \right) $

(48)

根据式（48）从初始条件开始计算，即可求得除了上、下边界条件外的任一时刻土壤剖面中的土壤体积含水量。

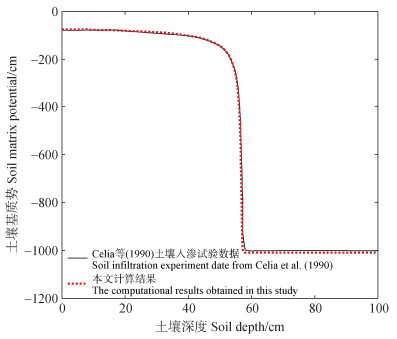
3 模型实现

依照上述编程思路即可实现有限元法求解两端点均为第一类边界条件的一维体积含水量型理查兹方程。根据Celia等^[10]试验资料，本文时间步长选取Δt=1 s，空间步长选取Δz=2.5 cm，程序运算总时长为86 400 s。本文采用MATLAB进行代码编写。将本文计算结果和Celia等^[10]土壤入渗试验数据进行对比（图 1），纳什效率系数=0.9998，纳什效率系数表示模拟值与实测值随时间变化的符合程度，因此证明本文提供的编程思路的可靠性。

4 结论

非饱和土壤水一维流动有限元法求解编程思路始于将权函数与理查兹方程相乘并在求解域上进行积分，得到的式（16）等价于式（1）。通过分部积分对式（16）进行降阶得式（19），式（19）可为代入自然边界条件提供便利。式（19）中的体积含水量对时间的导数项用后向差分法进行处理。再利用雅可比矩阵将积分区域转到[–1，1]上，为用高斯数值积分公式计算积分奠定基础。通过上述步骤得到的式（30）为非线性代数式，可用牛顿-拉夫逊法求解。牛顿-拉夫逊法中的求导数项用全微分法处理。最终构建了一个包含所有单元信息和边界条件的矩阵方程，通过代入已知第一类边界条件，基于式（48）可求解除边界外，任意时刻土壤剖面中的土壤体积含水量。相较于已发表的有关有限元法求解理查兹方程的学习材料^[12-17]，本文对上述编程思路给出了详细的描述，其中关于理查兹方程线性化和第一类边界条件处理的步骤对有限元法求解理查兹方程起着关键作用。

我国从事土壤物理研究的大部分学者本科毕业于农业资源与利用专业，数理基础不强，因而在土壤物理过程数值模拟上实现突破存在一定难度^[11]。本文结合实际情况针对上述问题进行了分析、讨论并提出了一个有益解决上述问题的思路。鉴于自学入门土壤物理过程数值模拟是上述研究人员的主要学习途径，本文以具有两个第一类边界条件的体积含水量为因变量的一维理查兹方程为例，详细描述了相关数值模拟编程思路并提供了相应代码。笔者认为本文提供的编程思路和代码（ScienceDB，https://doi.org/10.57760/sciencedb.21257）将会帮助与笔者背景相似的研究人员少走弯路，较快入门土壤物理过程数值模拟，以期为解决我国土壤物理过程数值模拟难以取得突破的问题起到一些积极作用。