2. 云南省高校高原山区空间信息测绘技术应用工程研究中心, 昆明 650093
2. Application Engineering Research Center of Spatial Information Surveying and Mapping Technology in Plateau and Mountainous Areas set by Universities in Yunnan Province, Kunming 650093, China
土壤作为地球上所有生态系统存在的基础,健康的土壤是实现人类社会可持续发展的关键因素之一[1-3]。然而矿产资源开发导致矿区土壤重金属污染严重,已成为亟待解决的环境难题[4]。如何快速准确获取矿区土壤中重金属含量空间分布信息,是制定治理措施和保障人民生命健康的前提。
传统的重金属含量检测方法,虽可揭示特定区域土壤重金属含量的空间分布信息,但由于操作过程复杂、成本高且缺乏时效性,因此难以实现对土壤重金属含量的实时、快速检测[5]。而高光谱遥感技术因光谱分辨率高、连续性强以及多波段同时成像能力等优势,能够准确反演土壤中重金属以及其他元素信息[6]。室内光谱反演重金属含量的研究作为野外光谱和遥感影像光谱反演土壤重金属含量的基础,也是目前大多数研究所聚焦的领域。野外光谱和遥感影像光谱易受温度、湿度、光照条件等环境因素干扰,数据稳定性与准确性难以保障,致使相应的研究成果在实际应用和推广中还处于探索阶段[7]。为了消除环境因素对光谱数据的影响,目前研究常用直接校正(Direct Standardization,DS)算法和分段直接校正(Piecewise Direct Standardization,PDS)算法对野外或影像光谱数据进行校正,取得较好的建模效果[8]。由于高光谱数据冗余度高、自相关性较强,不同预处理和特征变量优选方法能够有效突出光谱特征和优化波谱响应机制[9]。其中常用的预处理方法包括包络线去除、倒数对数、标准正态变换、一阶微分和二阶微分等。有研究表明,相较于传统的整数阶微分,使用分数阶微分(Fractional Order Derivative,FOD)能够更加敏锐地捕捉波段的曲率和斜率变化,在建模精度提升方面表现优异[10]。丁松滔等[11]研究表明,利用FOD处理影像光谱数据,并结合偏最小二乘法反演矿区重金属Pb、Zn、Ni具有可行性。蒋宇恒等[12]构建FOD模型对农田Zn、Ni含量开展反演研究,结果表明相较于整数阶微分,FOD建模效果更优。此外,Boruta特征变量优选算法可有效精简最优特征组合,对简化模型结构、提高模型稳定性和泛化能力效果显著[13-14]。Box-Cox变换作为一种有效的统计方法,能够显著提高重金属含量数据的正态性,为后续建模提供更为可靠的数据基础[15]。
目前,针对土壤重金属含量呈偏态分布区域以及利用DS算法消除高光谱影像数据受环境变量等因素干扰的系统性研究鲜有涉及。本文以云南省会泽县矿山镇某尾矿区为研究对象,在室内采集了56个表层土壤样本的高光谱数据以及Pb、Zn含量数据,同时收集高分5号(GF-5)影像光谱数据。首先使用DS算法联合室内光谱数据校正GF-5影像光谱数据,以及利用Box-Cox变换使Pb和Zn含量符合正态性;随后对校正后的光谱数据进行FOD光谱变换,并使用Boruta算法筛选特征波段;最后,构建随机森林(Random Forest,RF)和极限梯度提升树(eXtreme Gradient Boosting,XGBoost)反演模型。本研究目的包括:(1)基于室内光谱数据对星载高光谱数据进行校正,建立多源异质光谱数据的同化机制,消除大气传输与环境噪声引起的光谱畸变;(2)利用Box-Cox算法解决矿区重金属含量偏态分布问题;(3)通过FOD凸显更多细节光谱信息并结合Boruta算法筛选出最优特征波段组合;(4)系统性评估RF和XGBoost模型反演矿区土壤重金属含量的性能。
1 材料与方法 1.1 研究区概况和试验数据收集研究区位于云南省会泽县矿山镇某铅锌尾矿区(26°37′39″~26°38′56″N,103°42′17″~103°43′47″E),属于典型温带高原季风气候,年平均气温和降雨量分别为13℃和807mm。该区域铅锌矿床是川滇黔铅锌成矿区内典型的大型富铅锌矿床之一[16]。该矿区在开采和冶炼过程中,由于废气、废水、废料和尾矿的堆放及淋溶,导致矿区周围土壤重金属含量不同程度地超标,对周边生态环境造成了严重影响[17]。2024年3月,采用梅花形5点混合采样法(范围为:5 m×5 m)进行采样。采集深度为0~20 cm,去除石块、动植物残体等杂质后约取1 kg土样,共采集56个土壤样品,同时记录每个采样点的地理坐标及周围环境情况。研究区地理位置、采样点分布以及实地照片如图 1所示。

|
图 1 研究区位置和采样点分布示意图 Fig. 1 Schematic map of the study area location and distribution of sampling points |
将采集的土壤样品带回实验室,进行自然风干处理后,使用玛瑙研磨机将样品研磨过100目筛,以确保样品的均匀性和一致性。处理过后的样品分为两份,一份使用尼通XL3t 950手持矿石元素分析仪测定土壤中Pb和Zn的含量;另一份使用ASD Field Spec 3地物波谱仪测定光谱数据,波段范围为350 nm~2 500 nm,重采样间隔设置为1 nm,得到的波段数为2 151个。此外,本研究使用的高分5号(GF-5)高光谱影像采集于2024年3月9日,通过“国家遥感数据和应用服务平台”(https://www.cpeos.org.cn/home/#/)申请获取,其空间分辨率为30 m,波段范围为400~2 500 nm,共330个波段。获取的影像数据需经过完整的预处理流程:首先对影像数据进行辐射定标、大气校正和正射校正;随后进行光谱重采样,使其与室内测定光谱具有相同的光谱分辨率,确保数据的可比性和分析的准确性。
1.2 直接校正算法DS算法是一种对光谱直接校正的算法,可以通过实验室测定的室内光谱来校正野外光谱或高光谱影像光谱,从而消除环境因素对光谱的影响[13]。本研究室内光谱(Xlab)和GF-5影像光谱(XGF5)的矩阵维度均为n×p,其中n为转换光谱的数量,p为波段的数量。室内和影像光谱的DS转换关系式为:
| $ X_{\mathrm{lab}}=X_{\mathrm{GF} 5} B+E $ | (1) |
式中,B为由Xlab和XGF5共同决定的未知参数转换矩阵,维度为P×P;E为背景残差矩阵,表示为:
| $ E=\lambda d_S^T $ | (2) |
式中,ds为由基线差异产生的P×1的矩阵;λ为所有列向量值均为1的n×1的矩阵。将式(2)代入式(1)可得:
| $ X_{\mathrm{lab}}=X_{\mathrm{GF} 5}+\lambda d_S^T $ | (3) |
为了计算未知的转换矩阵B,首先需要引入一个n×n阶的中心化矩阵Cn,可表达为:
| $C_n=I_n-\left(\frac{1}{n}\right) \lambda \lambda^{\mathrm{T}} $ | (4) |
式中,In为一个n×n的单位矩阵。将式(3)两边同时乘以Cn,因Cnλ
| $ {\bar X_{{\text{lab}}}} = {\bar X_{{\text{GF5}}}}B $ | (5) |
经过最小二乘变为:
| $ B = \bar X_{{\text{GF5}}}^ + {\bar X_{{\text{lab}}}} $ | (6) |
式中,+表示
| $ {d_s} = \bar X_{{\text{lab}}}^T - {B^T}\bar X_{{\text{GF5}}}^T $ | (7) |
式中,
最终经过上述DS转换后的影像光谱可表示为:
| $ X_{\mathrm{lab}}^{\prime}=X_{\mathrm{GF} 5} B+\mathrm{E} $ | (8) |
分数阶微分(FOD)将传统整数阶微分推广至任意阶,在光谱分析时能够更加敏锐地捕捉到光谱反射率细节的变化。常用的分数阶微分方法主要包括:Riemann-Liouville(R-L)、Grunwald-Letnikov(G-L)和Caputo[18]。其中,G-L基于无穷级数进行定义,适合数值计算,能够处理复杂的信号和系统,因此是在光谱分析中进行FOD计算的常用方法。
1.4 建模方法本文使用Boruta特征变量优选算法进行特征波段筛选[13],构建了随机森林(Random Forest,RF)和极限梯度提升树(eXtreme Gradient Boosting,XGBoost)反演模型[10],预测研究区内土壤Pb和Zn的含量。模型精度的评价指标选择决定系数(R2)、均方根误差(RMSE)和相对预测偏差(RPD)。其中,RPD值将模型预测性能分为三类:A类(RPD > 2.0),表示预测能力较强;B类(1.4 < RPD < 2.0),表示预测能力中等;C类(RPD < 1.4),表示预测能力较弱[14]。
2 结果 2.1 土壤中Pb和Zn原始含量及Box-Cox变换后含量的统计特征研究区Pb和Zn含量的统计特征结果见表 1。对于原始数据,Pb含量范围为17.95~33442.41 mg.kg–1,标准差为7086.17 mg.kg–1,偏度为2.92;Zn含量范围为45.85~58647.12 mg.kg–1,标准差为11628.44 mg.kg–1,偏度为3.23。在土壤调查中,变异系数(Coefficient of Variance,CV)能够有效反映土壤中重金属含量的空间分布差异[19];Pb和Zn的CV均超过100%,其含量在该研究区内呈现高度变异,说明其空间分布差异较大;Pb和Zn的Pearson相关系数达到0.82(P < 0.01)。经过Box-Cox转换后,Pb和Zn含量的范围跨度显著减小,数据由高度变异转变为中度变异,偏度也接近于0,说明转换后的数据更符合正态分布,同时Pearson相关系数提升0.09,进一步凸显了二者之间的关联性。
|
|
表 1 Pb和Zn含量的统计特征 Table 1 The statistical characteristics of Pb and Zn content |
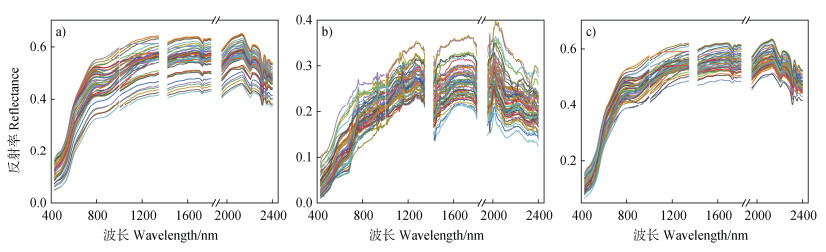
光谱数据在采集过程中容易受仪器、人为操作以及外部环境等诸多因素的影响,导致测定的光谱反射率中混入大量随机噪声,因此需对室内光谱数据和影像光谱反射率进行预处理。首先采用Savitzky-Golay(SG)滤波技术对光谱数据进行平滑处理,以降低噪声的影响;其次,在350~429 nm、996~1 005 nm和2 401~2 500 nm的波段范围内,受到传感器自身缺陷的影响,光谱反射率出现明显的振荡,导致其信噪比降低。此外,由于水汽的强烈吸收作用,在1 344~1 424 nm和1 804~1 954 nm的波段中,光谱反射率出现了明显的“阶跃”现象,因此需要将这些波段从后续的处理流程中排除;室内和影像光谱数据经过上述处理后,保留的有效波段数为1 733个,图 2a和图 2b分别展示了经过预处理后的室内光谱和GF-5影像光谱反射率。预处理完成后,运用DS算法结合室内光谱数据对GF-5影像数据进行光谱校正,校正后的影像光谱数据如图 2c所示,不仅提升了影像光谱反射率波形与室内光谱反射率之间的相似度,而且使得影像光谱曲线更为平滑,反射率也有显著提高。这充分表明,DS能够有效抑制土壤粒径、含水量和温度等环境因素对影像光谱反射率的影响。将经过以上处理后的影像光谱反射率作为原始光谱反射率(Origin spectral reflectance,OR),并将其应用于后续的建模分析。
|
图 2 实验室光谱曲线(a)、GF-5影像光谱曲线(b)和校正后光谱曲线(c) Fig. 2 Laboratory spectrum curve(a), GF-5 image spectrum curve(b), and corrected spectrum curve(c) |
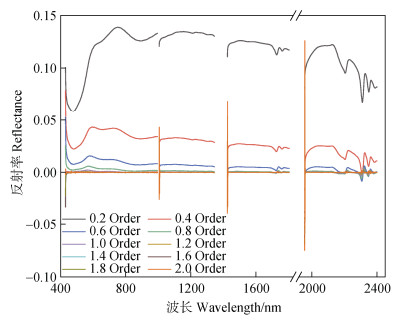
图 3展示了使用G-L分数阶微分方法对OR进行光谱变换的结果。在0~2阶的范围内,以0.2阶为步长进行10次光谱变换。结果表明,随着微分阶数的增加,光谱反射率逐渐降低并趋近于零,波峰和波谷的特征逐渐鲜明,但其强度差异逐渐减小,这一变化规律符合G-L定义的数学原理:当微分步长小于波峰和波谷的固有宽度时,细微的光谱差异被逐阶放大,光谱特征会被显著增强[20]。然而值得注意的是,高阶微分(≥1.0阶)会放大波段间差异较大的噪声信号,尤其是1 400 nm和2 000 nm附近出现显著的高频噪声干扰。相比之下,低阶微分(如0.2阶和0.4阶)生成的光谱曲线更为平滑,噪声较小。因此,不同阶数的G-L分数阶微分在增强光谱特征和抑制噪声方面表现出显著差异,这为基于光谱特征的土壤分析提供了分数阶微分的优化选择依据。
|
图 3 各阶次分数阶微分光谱曲线 Fig. 3 Fractional order derivative spectral curves of different orders |
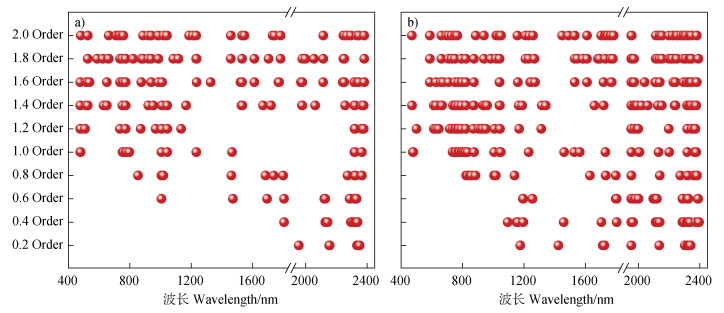
对OR进行分数阶微分处理后,运用Boruta算法筛选特征波段。如图 4所示,经Boruta算法筛选得到的Pb和Zn特征波段分布基本一致,其中高阶筛选获得的特征波段数量较多,而低阶筛选获得的相对较少。使用高阶微分(≥1.0阶)时,两种重金属元素特征波段主要集中在700~1 000 nm、1 400~1 750 nm和2 250~2 400 nm范围内,而低阶微分处理下,特征波段少部分位于可见光区域,更多集中于近红外和短波红外区域。
|
图 4 Boruta算法选取的Pb(a)和Zn(b)特征波长分布 Fig. 4 Distribution of feature wavelengths selected by the Boruta Algorithm for Pb(a)and Zn(b) |
本次研究采用RF和XGBoost算法构建矿区土壤中Pb和Zn含量的估算模型,所有模型均在Python的scikit-learn和XGBoost库中实现。模型以Boruta算法筛选的各阶次特征波段作为自变量,转换后Pb和Zn的含量为因变量,其中70%为训练集,30%为验证集。
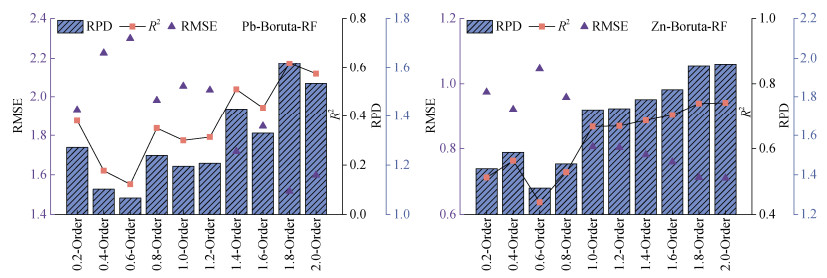
图 5展示了RF模型在不同微分阶数下对Pb和Zn含量估算的各项指标,随着微分阶数的增加,Pb和Zn的R2呈现先下降后逐渐上升的趋势。对于Pb,模型精度在1.8阶时最高,验证集的R2为0.618,RMSE为1.517,PRD为1.618,其次是1.4阶和2阶的R2分别为0.51和0.575,RMSE分别为1.517和1.718,RPD分别为1.535和1.618;1.4阶、1.8阶和2阶的PRD均介于1.4和2.0之间,说明对Pb的预测能力中等,而其余阶数的RPD小于1.4,则模型预测能力较差。对于Zn,模型精度在2阶时最高,验证集的R2为0.741,RMSE为0.71,PRD为1.965,预测能力中等;在0.6阶时,其RPD小于1.4,预测能力较差;而其余阶数的RPD均介于1.4和2之间,表明其对Zn含量的预测能力中等。
|
图 5 不同微分阶数下RF模型对Pb和Zn含量估算的各项指标 Fig. 5 Evaluation metrics for the estimation of Pb and Zn content using the RF model at different differential orders |
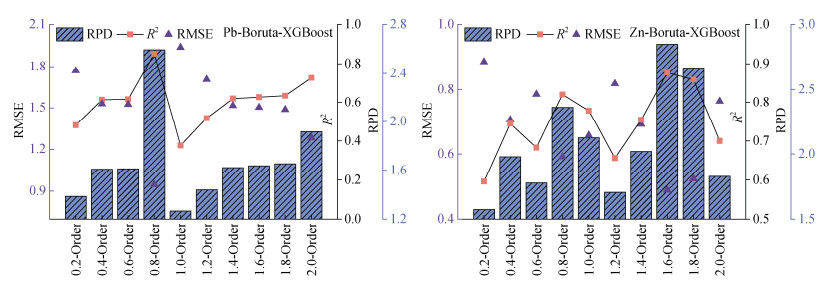
图 6展示了XGBoost模型在不同微分阶数下对Pb和Zn估算的各项指标,对于Pb,在0.8阶时模型精度最高,其验证集的R2为0.852,RMSE为0.946,PRD为2.595,其预测能力较好(RPD > 2.0);0.4阶、0.6阶、1.2阶、1.4阶、1.6阶、1.8阶和2阶预测能力中等(1.4 < RPD < 2.0);0.2阶和1.0阶预测能力较差(RPD < 1.4)。对于Zn,在1.6阶时模型精度最高,其验证集的R2为0.877,RMSE为0.489,PRD为2.849;0.8阶、1阶、1.4阶、1.6阶和1.8阶其预测能力较好(RPD > 2.0);0.2阶、0.4阶、0.6阶、1.2阶和2阶预测能力中等(1.4 < RPD < 2.0)。
|
图 6 不同微分阶数下XGBoost模型对Pb和Zn含量估算的各项指标 Fig. 6 Evaluation metrics for the estimation of Pb and Zn content using the XGBoost model at different differential orders |
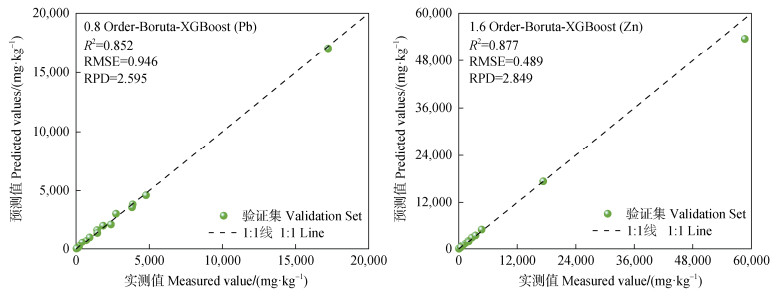
为了更加直观地展示模型在预测Pb和Zn含量方面的性能,绘制了Pb和Zn最佳反演模型验证集的实测值和预测值拟合图(见图 7)。从图中可以看出,预测值和实测值基本分布在1:1直线周围,表明模型具有较高的预测精度。因此将0.8 Order-Boruta-XGBoost和1.6 Order-Boruta-XGBoost分别作为预测该矿区Pb和Zn含量的最佳反演模型,可有效揭示研究区内铅锌含量的分布情况。
|
图 7 实测值和预测值的拟合图 Fig. 7 Fitting plot of the measured and predicted values |
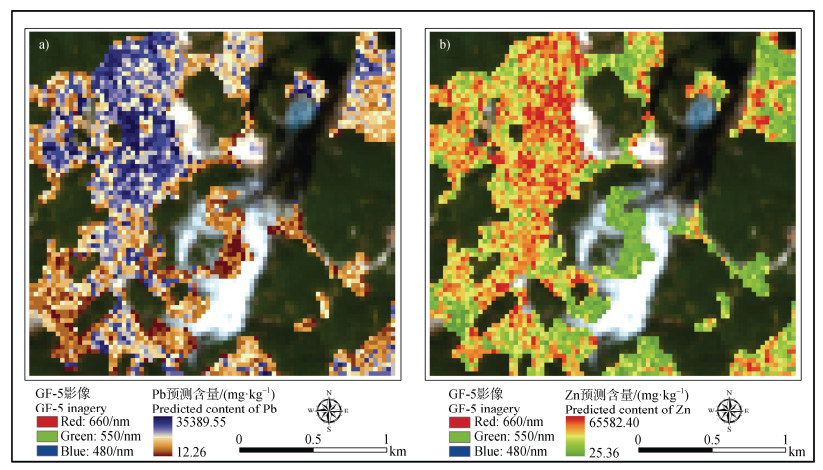
运用最佳反演模型对研究区内裸土区域Pb和Zn含量进行估算(见图 8)。结果显示,研究区西北部Pb和Zn含量明显高于其他区域,是污染最为严重的区域;从实地调查获取的信息(见图 1)为该结论提供了有力支撑,西北部区域曾是历史遗留的采矿和冶炼场地,堆积了大量废渣和废料,因此人类活动是导致该区域重金属污染严重的主要原因。将Pb和Zn的Pearson(P < 0.01)相关系数达到0.82(见表 1)与反演结果的空间分布特征进行分析,两种重金属的高度相关性和空间分布一致性揭示了它们可能具有复合污染特征或同源性。以上均从不同角度验证了最佳反演模型的准确性和可靠性。
|
图 8 应用最佳反演模型估算的Pb(a)和Zn(b)含量分布图 Fig. 8 Distribution map of Pb(a)and Zn(b)content estimated by the optimal inversion model |
本研究以云南会泽县矿山镇某铅锌尾矿区为例,采用DS算法结合室内光谱数据对GF-5影像光谱数据进行校正,消除多种环境因素对影像光谱的干扰。通过这一方法,旨在获得更加纯净的高光谱数据,从而更加准确地反演研究区内Pb和Zn含量的空间分布。研究表明,使用DS算法能够消除土壤粒径、含水量和温度等环境因素对影像光谱反射率的影响,从而有效地提升了模型精度,这与Zhang等[13]的研究结果一致。
由于受人为活动的影响,土壤重金属含量通常呈偏态分布。在这种情况下直接利用原始光谱数据与重金属实测值构建反演模型,不仅会增加模型的复杂性和计算难度,还可能因为含量数据不符合正态分布而导致模型精度降低,无法准确反映研究区的重金属含量空间分布情况。使用Box-Cox转换能够使重金属含量服从正态分布,从而提高反演结果的准确性[15]。
在分数阶微分处理中,高阶微分能够突出信号中的高频变化,有助于揭示更多显著的特征波段,这些波段通常包含丰富的细节信息,有助于区分不同物质或元素的光谱特征。相比之下,低阶微分(0.2阶~1阶)则保留光谱的整体趋势和平滑变化,忽略了细微波动,导致许多波段的特征变化不明显,从而使用Boruta算法筛选出的特征波段数量较少。
RF和XGBoost是两种被广泛应用的集成学习算法。RF通过构建多棵决策树,并利用投票机制对数据进行预测,虽然在高维数据和处理多样化特征方面表现良好,但在面对复杂的非线性关系时,其效果通常不如梯度提升类算法。相比之下,XGBoost是基于梯度提升树(GBDT)的改进算法,通过逐步拟合残差构建新树,并采用加权优化来增强模型性能;同时,XGBoost还引入了正则化(L1/L2正则化)、树的深度限制、列抽样等技术,能够有效防止过拟合,从而提高了模型的鲁棒性和精度。由于高光谱数据与重金属含量之间存在众多复杂的非线性关系,XGBoost在此类任务中通常优于RF,尤其是在处理复杂特征交互和非线性模式时表现更为出色。
4 结论(1)通过DS算法建立室内测定光谱和GF-5影像光谱之间的定量关系,从而有效消除土壤粒径、含水量和温度等环境因素对影像光谱数据的干扰。同时,Box-Cox转换解决了重金属含量数据的偏态分布问题,使其更加接近正态分布。两种数据预处理方法共同为更加准确地反演矿区土壤中重金属含量奠定了坚实基础。(2)使用分数阶微分构建的反演模型精度基本优于传统整数阶微分模型,表明不同阶数的分数阶微分能够增强土壤重金属光谱中的微弱信息,从而使Boruta算法能更好地捕捉到细节光谱特征,提升了模型精度。(3)该研究区土壤Pb含量的最佳反演模型为0.8 Order-Boruta-XGBoost,而Zn含量的最佳反演模型为1.6 Order-Boruta-XGBoost。这两种最佳反演模型在该矿区Pb和Zn含量反演中表现出较高的精度和较强鲁棒性,绘制的Pb和Zn含量空间分布图与实地调查结果相吻合。
| [1] |
Wu Y F, Li X, Yu L, et al. Review of soil heavy metal pollution in China: Spatial distribution, primary sources, and remediation alternatives[J]. Resources, Conservation and Recycling, 2022, 181: 106261. DOI:10.1016/j.resconrec.2022.106261
(  0) 0) |
| [2] |
Li Y Z, Zhang J Z, Jia J Y, et al. Research progresses on farmland soil ecosystem multifunctionality (In Chinese)[J]. Acta Pedologica Sinica, 2022, 59(5): 1177-1189. DOI:10.11766/trxb202109290532 [李奕赞, 张江周, 贾吉玉, 等. 农田土壤生态系统多功能性研究进展[J]. 土壤学报, 2022, 59(5): 1177-1189.]
(  0) 0) |
| [3] |
Chang C Y, Yang J, Wu J, et al. Deliberations on collaborative supervision of risk control and remediation for soil pollution of constructed land (In Chinese)[J]. Acta Pedologica Sinica, 2025, 62(5): 1-13. DOI:10.11766/trxb202408280345 [常春英, 杨婕, 吴俭, 等. 建设用地土壤污染风险管控和修复联动监管的若干思考[J]. 土壤学报, 2025, 62(5): 1-13.]
(  0) 0) |
| [4] |
Wang Y J. Research progress and prospect on ecological disturbance monitoring in mining area (In Chinese)[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1705-1716. [汪云甲. 矿区生态扰动监测研究进展与展望[J]. 测绘学报, 2017, 46(10): 1705-1716.]
(  0) 0) |
| [5] |
Liu Z H, Lu Y, Peng Y P, et al. Estimation of soil heavy metal content using hyperspectral data[J]. Remote Sensing, 2019, 11(12): 1464. DOI:10.3390/rs11121464
(  0) 0) |
| [6] |
Jin M T, Yuan H, Liu B, et al. Review of the distribution and detection methods of heavy metals in the environment[J]. Analytical Methods, 2020, 12(48): 5747-5766. DOI:10.1039/D0AY01577F
(  0) 0) |
| [7] |
Zhang X, Ding S T, Cen Y, et al. Soil heavy metal Pb content estimation method by combining field spectra with laboratory spectra (In Chinese)[J]. Geomatics and Information Science of Wuhan University, 2022, 47(9): 1479-1485. [张霞, 丁松滔, 岑奕, 等. 结合野外与实验室光谱的土壤Pb含量反演[J]. 武汉大学学报(信息科学版), 2022, 47(9): 1479-1485.]
(  0) 0) |
| [8] |
Shi Y Y, Li J Y, Chu X L. Progress and applications of multivariate calibration model transfer methods (In Chinese)[J]. Chinese Journal of Analytical Chemistry, 2019, 47(4): 479-487. [史云颖, 李敬岩, 褚小立. 多元校正模型传递方法的进展与应用[J]. 分析化学, 2019, 47(4): 479-487.]
(  0) 0) |
| [9] |
Sun G Y, Fu H, Zhang A Z, et al. Singular spectrum analysis method for hyperspectral imagery feature extraction: A review and evaluation (In Chinese)[J]. Acta Geodaetica et Cartographica Sinica, 2023, 52(7): 1148-1163. [孙根云, 付航, 张爱竹, 等. 高光谱影像奇异谱分析特征提取方法: 综述与评价[J]. 测绘学报, 2023, 52(7): 1148-1163.]
(  0) 0) |
| [10] |
Chen L H, Lai J, Tan K, et al. Development of a soil heavy metal estimation method based on a spectral index: Combining fractional-order derivative pretreatment and the absorption mechanism[J]. Science of the Total Environment, 2022, 813: 151882. DOI:10.1016/j.scitotenv.2021.151882
(  0) 0) |
| [11] |
Ding S T, Zhang X, Shang K, et al. Estimating soil heavy metal from hyperspectral remote sensing images base on fractional order derivative (In Chinese)[J]. Journal of Remote Sensing, 2023, 27(9): 2191-2205. [丁松滔, 张霞, 尚坤, 等. 基于分数阶微分的土壤重金属高光谱遥感图像反演[J]. 遥感学报, 2023, 27(9): 2191-2205.]
(  0) 0) |
| [12] |
Jiang Y H, Yan B, Zhuang Q Y, et al. Quantitative inversion model of soil heavy metals Zn and Ni based on fractional order derivative (In Chinese)[J]. Spectroscopy and Spectral Analysis, 2024, 44(10): 2850-2857. [蒋宇恒, 晏博, 庄清源, 等. 基于分数阶微分的土壤重金属锌和镍的定量反演模型研究[J]. 光谱学与光谱分析, 2024, 44(10): 2850-2857.]
(  0) 0) |
| [13] |
Zhang B, Guo B, Zou B, et al. Retrieving soil heavy metals concentrations based on GaoFen-5 hyperspectral satellite image at an opencast coal mine, Inner Mongolia, China[J]. Environmental Pollution, 2022, 300: 118981. DOI:10.1016/j.envpol.2022.118981
(  0) 0) |
| [14] |
Mao J H, Zhao H Q, Jin Q, et al. Comparative study on the hyperspectral inversion methods for soil heavy metal contents in Hebei lead-zinc tailings reservoir areas (In Chinese)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2023, 39(22): 144-156. [毛继华, 赵恒谦, 金倩, 等. 河北铅锌尾矿库区土壤重金属含量高光谱反演方法对比[J]. 农业工程学报, 2023, 39(22): 144-156.]
(  0) 0) |
| [15] |
Zhao H L, Gan S, Yuan X P, et al. Prediction of low Zn concentrations in soil from mountainous areas of central Yunnan Province using a combination of continuous wavelet transform and Boruta algorithm[J]. International Journal of Remote Sensing, 2023, 44(15): 4753-4774. DOI:10.1080/01431161.2023.2237664
(  0) 0) |
| [16] |
Han R S, Wu P, Zhang Y, et al. New research progress in metallogenic theory for rich Zn-Pb-(Ag-Ge)deposits in the Sichuan-Yunnan-Guizhou Triangle(SYGT)area, southwestern Tethys (In Chinese)[J]. Acta Geologica Sinica, 2022, 96(2): 554-573. [韩润生, 吴鹏, 张艳, 等. 西南特提斯川滇黔成矿区富锗铅锌矿床成矿理论研究新进展[J]. 地质学报, 2022, 96(2): 554-573.]
(  0) 0) |
| [17] |
Chen W, Liu Q, Wang B, et al. Evaluation and source analysis of heavy metal pollution in cultivated soil of a lead-zinc mining area in Huize County, Yunnan Province, China (In Chinese)[J]. Journal of Agro-Environment Science, 2024, 43(5): 1036-1044. [陈文, 刘奇, 王豹, 等. 云南省会泽县某铅锌矿区耕地土壤重金属污染评价及来源解析[J]. 农业环境科学学报, 2024, 43(5): 1036-1044.]
(  0) 0) |
| [18] |
Benkhettou N, Brito da Cruz A M C, Torres D F M. A fractional Calculus on arbitrary time scales: Fractional differentiation and fractional integration[J]. Signal Processing, 2015, 107: 230-237. DOI:10.1016/j.sigpro.2014.05.026
(  0) 0) |
| [19] |
Liu J L, Liu L, Ma X Y, et al. Spatial variability of soil salt in different soil layers at different scales (In Chinese)[J]. Journal of Basic Science and Engineering, 2018, 26(2): 305-312. [刘继龙, 刘璐, 马孝义, 等. 不同尺度不同土层土壤盐分的空间变异性研究[J]. 应用基础与工程科学学报, 2018, 26(2): 305-312.]
(  0) 0) |
| [20] |
Jalalinejad H, Tavakoli A, Zarmehi F. A simple and flexible modification of Grünwald–Letnikov fractional derivative in image processing[J]. Mathematical Sciences, 2018, 12(3): 205-210. DOI:10.1007/s40096-018-0260-6
(  0) 0) |
 2026, Vol. 63
2026, Vol. 63


