2. 西北农林科技大学水土保持与荒漠化整治全国重点实验室, 陕西杨凌 712100;
3. 西北农林科技大学资源环境学院, 陕西杨凌 712100;
4. 重庆文理学院化学与环境工程学院, 重庆 402160
2. State Key Laboratory of Soil and Water Conservation and Desertification Control, Northwest A&F University, Yangling, Shaanxi 712100, China;
3. College of Resources and Environment, Northwest A&F University, Yangling, Shaanxi 712100, China;
4. College of Chemistry and Environmental Engineering, Chongqing University of Arts and Sciences, Chongqing 402160, China
土壤中纳米/胶体颗粒表面带有大量电荷,这些电荷使颗粒表面周围吸附与表面电荷符号相反的离子(反离子),从而在固-液界面中形成双电层。研究表明,外电场可诱导原子/分子中电子轨道的重排(杂化),继而产生新的界面相互作用[1-2]。轨道杂化使原子/离子外层电子出现能级分裂,电子跃迁至离核较远的高能级杂化轨道。土壤表面的非均匀电场通过吸引原子核同时排斥外层电子,使电荷中心发生相对位移而形成偶极矩,即产生极化现象。处于极化状态的原子/离子,其高能级外层电子若与邻近原子/离子/分子满足能级匹配条件(轨道能量相近且波函数相位一致),则可通过电子云重叠形成新型化学键合,称为极化诱导共价键(Polarization-induced covalent bonding,PICB)。例如,黏土矿物表面存在大量的硅氧烷型表面氧(O)原子,这些O原子的外层孤对电子能量低而表现出非常弱的路易斯碱性,难以形成稳定的经典共价键。但是,黏土矿物表面强电场会提高表面O原子孤对电子的活性,使孤对电子偏向吸附在表面H+的1s低能级轨道,产生量子干涉而形成PICB。该共价键是电场依赖型共价键,其强度随电场增强而增大,与经典共价作用有本质区别[3]。
在土壤颗粒表面电荷形成的强电场作用下,吸附态反离子发生极化而形成新的成键轨道,其化学性质亦发生改变[4-5]。例如,重金属阳离子在黏土矿物表面电场作用下产生轨道杂化效应,增强了重金属离子的极化,进而与矿物表面产生极化与极化诱导共价作用[6-7]。极化与极化诱导共价作用增强离子-表面相互作用力以及屏蔽表面电场的能力,进而调控固-液界面性质和结构[8]。土壤固-液界面结构与性质主导着离子-表面相互作用类型与强度,对离子的吸附固定具有重要影响[9-11]。例如,土壤颗粒表面强电场增加了矿物表面O原子外层孤对电子的活性[3],使H+-矿物表面O相互作用对矿物结构稳定性具有重要贡献,从而影响矿物风化过程[12]。离子-表面相互作用进一步调控土壤颗粒-颗粒相互作用,颗粒相互作用对土壤众多过程密切相关[13]。例如,土壤团聚体稳定性[14-16]、土壤水分运动[17-18]、纳米塑料的迁移[8,19]、土壤侵蚀与农田面源污染[20-21]等。基于轨道杂化效应的土壤固-液界面反应对离子-土壤颗粒、土壤颗粒-颗粒相互作用,以及土壤系列宏观表现均具有重要影响,从而实现对土壤环境的多尺度耦合、多过程关联的系统性描述。因此,土壤固-液界面原子/离子轨道杂化效应具有重要的环境意义。
本文通过土壤固-液界面结构和性质,以及土壤电场中原子/离子轨道杂化的定量描述,进一步阐明离子界面反应的量子力学机制,明确其对矿物风化与土壤酸化、土壤重金属钝化/活化、土壤水盐运移等宏观现象的重要调控作用,以期阐明土壤中微观界面反应与宏观现象的多尺度耦合和多过程关联。
1 土壤固-液界面结构土壤胶体是由矿物质、有机质、微生物及其复合体等颗粒组成,表面带有同晶替代、质子吸附/解吸、专性吸附等产生的电荷。这些电荷在土壤颗粒表面通常能产生上亿伏特每米的强电场[22]。反离子的吸附中和了表面电荷,使土壤颗粒与反离子及其介质一起形成表观不带电的中性体系。但是,由于热运动的存在,反离子并非与表面电荷位点直接接触,而是在颗粒表面附近区间呈扩散状分布,即玻尔兹曼(Boltzmann)分布[23]。土壤颗粒表面电荷与扩散层中的反离子共同组成具有一定空间的界面扩散层。
尽管表面存在强电场,但是人们并未感受到土壤带电,这是因为尺寸效应无法进入界面扩散层。一般情况下,扩散层的厚度能够达到几十至上百纳米,与土壤溶液离子组成、浓度、温度等有关[24]。扩散层中吸附的反离子能够屏蔽电场,同时电场也会对反离子的外层电子轨道产生杂化[6-7]。该作用可增强离子吸附能力和屏蔽电场能力[25],通过扩散层中离子分布、电位分布以及电场分布影响固-液界面性质和结构[26]。
基于平板平面、均匀介质、库仑力、离子点电荷假设的Gouy-Chapman理论通过界面化学中的泊松-玻尔兹曼方程(Poisson-Boltzmann,PB方程)对土壤固-液界面结构进行定量描述(图 1),包括双电层中的浓度分布、界面电位与电位分布、表面电荷密度与表面电场强度等。
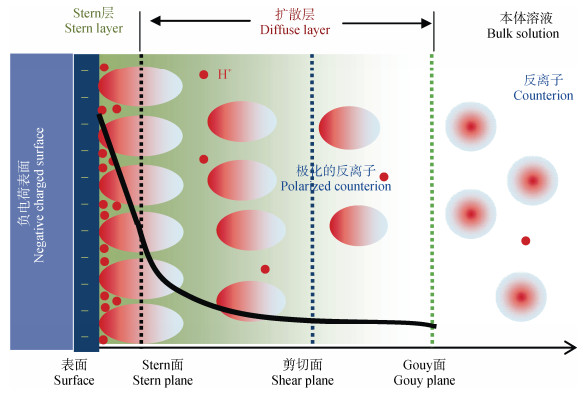
|
注:扩散层中反离子的形变表示在表面负电场中发生极化,实线表示电位分布曲线。 Note: The deformation of counterions in the diffuse layer represents the occurrence of polarization effects in the negative electric field at the surface. The solid line denotes the potential distribution. 图 1 固-液界面结构示意图 Fig. 1 Schematic diagram of solid-liquid interface structure |
平衡状态下,离子在双电层中的分布遵循Boltzmann方程,将Boltzmann方程代入Poisson方程,即为PB方程。早在1910—1913年间,Gouy[27]和Chapman[28]首先获得了PB方程在单一对称电解质中的解析解:
| $ \varphi (x) = (4RT/ZF){\tanh ^{ - 1}}({\lambda _{Z:Z}}{e^{ - Z\kappa x}}) $ | (1) |
其中,
| $ λ_{Z:Z}=\tanh(ZFφ_{0}/4RT)$ | (2) |
式中,R为气体常数,单位J·mol–1·K–1;T为绝对温度,单位K;φ0为带电粒子的表面电位(本文指扩散层起始面的电位),单位V;Z为反离子的化合价;F为法拉第常数,单位C·mol–1;φ(x)为距离颗粒表面x处的电位,单位V;κ=(8πF2Z2c0/εRT)1/2,c0为本体溶液反离子浓度,单位为mol·L–1;ε为介质的介电常数,单位C2·J–1·dm–1。
Grahame[29]获得了1︰2与2︰1型非对称电解质体系PB方程的解析,十余年前本课题组也获得了一价与二价离子混合电解质体系下(1︰1+1︰2、1︰1+2︰1、1︰1+2︰2、2:1+1︰2、2︰1+2︰2和1︰2+2︰2)扩散层中电位分布的解析表达式[30]。上述混合电解质体系的电位分布解析表达式是Gouy-Chapman理论的重要补充,在界面化学中至关重要。近期,研究人员基于Gouy-Chapman-Stern理论模型,研发了一种二维材料-水界面Zeta电位的原位可视化和精准定量分析的光学表征方法,利用原位光学成像技术,从微观可视化、动态监测以及材料本征特性与环境因素关联等角度为揭示固-液界面电位分布规律提供了新视角[31]。从不同角度对Gouy-Chapman理论进行了补充和拓展,使其在更多场景下具有更强的解释力和应用价值。
1.2 表面电荷密度与表面电场表面电荷数量(N0)与比表面积(S)的比值即为土壤颗粒的表面电荷密度(σ0):
| $ {\sigma _0} = \frac{{{N_0}}}{S} $ | (3) |
根据高斯定理,表面电场强度(ζ)为:
| $ \zeta = \frac{{4\pi }}{\varepsilon }{\sigma _0} $ | (4) |
土壤颗粒表面一般带负电,表面电荷数量在数值上约等于阳离子交换量,但符号相反。例如,某种土壤阳离子交换量为10 cmol(+)·kg–1,其表面负电荷数量近似为10 cmol(-)·kg–1,比表面积为50 m2·g–1,则溶液中土壤颗粒表面电荷密度与表面电场强度分别为0.193 C·m–2与2.724 × 108 V·m–1。土壤颗粒的表面电荷密度多数在0.1~0.4 C·m–2范围,水体系表面电场强度范围为1.411 × 108~5.645 × 108 V·m–1。由于颗粒表面水分子的极化作用,导致颗粒表面介电不饱和(非均匀介质),颗粒表面介电常数约为6.67 × 10–10 C2·J–1·m–1[26],因此,土壤表面电场强度一般在1.88 × 109~7.53 × 109 V·m–1,表明土壤是一个强电场体系。
1.3 界面电位(表面电位与Zeta电位)土壤固-液界面电位(表面电位和Zeta电位)是重要的电化学性质参数,在研究离子-表面相互作用、颗粒间相互作用及其环境效应等方面至关重要。因此,定量评估界面电位对了解土壤颗粒迁移、营养元素的保持与淋失、水土流失与农田面源污染、土壤酸化等问题均具有重要作用。
Zeta电位可通过电泳实验进行测定[32],已有大量文献关于Zeta电位的测定,本文不再赘述。一般情况下,Zeta电位为固-液界面中剪切面处的电位,表面电位为扩散层起始面(Stern面)的电位(图 1)。Zeta电位通常远低于表面电位,取决于表面电荷密度与电解质组成和浓度[33]。
对已知电解质组成,表面电位可通过电位分布进行积分求解[34-35],但是该方法依赖于电解质中反离子的吸附平衡。根据PB方程,只要获得表面电荷密度,可由如下通式评估表面电位:
| $ {\sigma _0} = \text{sgn} ({\varphi _0})\sqrt {\frac{{\varepsilon RT}}{{2\pi }}\sum\limits_i {(c_i^0{{\exp }^{ - {Z_i}F{\varphi _0}/RT}} - 1)} } $ | (5) |
式中,ci0表示本体溶液中离子i的浓度,单位mol·m–3。
2 土壤电场中原子轨道杂化上述土壤固-液界面结构的描述是基于经典双电层理论,未考虑外电场对离子/原子结构的改变。将离子/原子置于外电场中,其发射的光谱线会发生分裂,即斯塔克(Stark)效应[36]。Stark效应会产生新的能级和对应的轨道。吸附在土壤胶体表面的离子也必然受到表面强电场的影响而产生Stark效应,同时也会改变土壤胶体表面电位,进而改变界面中浓度分布和电位分布。
多电子离子外层轨道的哈密顿(Hamilton)算符需考虑电场的贡献,基于微扰理论,求解薛定谔方程获得外层2s2p的原子/离子(如-N、-O、-F、Na+、Mg2+等)(图 2a)[37]、3s3p的原子/离子(如-P、-S、-Cl、K+、Ca2+等)(图 2b)[37]、3s3p3d的离子(如Cr3+、Cu2+、Zn2+等)杂化轨道及能量(图 2c)[6]。量子力学分析发现,外电场中原子/离子确实发生了波函数的重排和能级的分裂。上述三种情形的波函数分别如图 2所示。
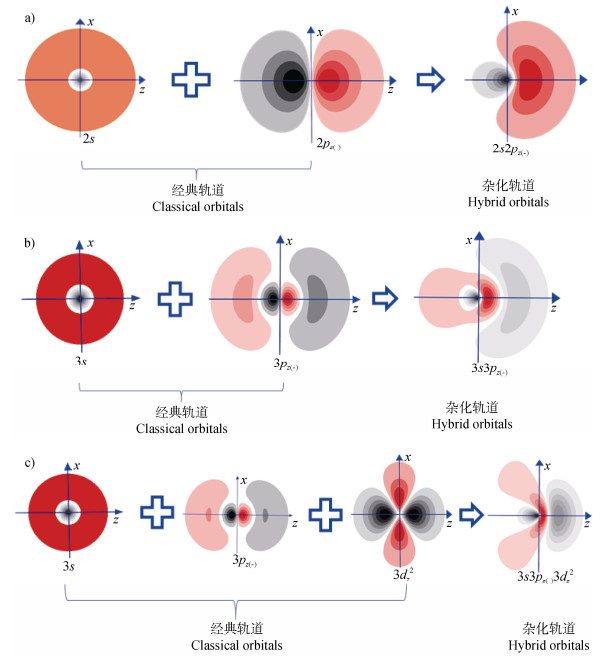
|
注:着色区域代表电子密度分布,颜色越深,电子密度越高。红色和黑色分别表示波函数的负值和正值。下同。 Note: The colored regions represent the electron density distribution, with darker shades indicating higher electron density. Red and black denote the negative and positive values of the wave function, respectively. The same below. 图 2 外电场中2s + 2p(a)、3s + 3p(b)以及3s + 3p + 3d(c)的经典轨道和杂化轨道 Fig. 2 The classical and hybrid orbitals of 2s + 2p (a), 3s + 3p (b), 3s + 3p + 3d (c) in an external electric field |
与经典轨道能量E30相比,基于3s3pz+3dz2的非对称杂化,n = 3重金属离子的非对称杂化轨道与经典轨道能量差为
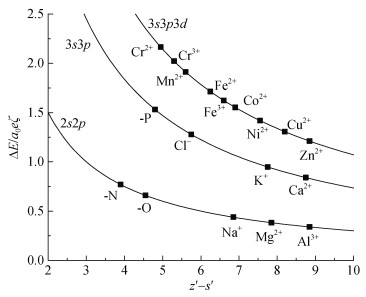
|
注:z′为核电荷数,s′为屏蔽常数,ΔE为经典轨道与杂化轨道的能量差,a0为玻尔半径,ζ为表面电场强度。 Note: z′ denotes the nuclear charge number, s′ represents the shielding constant, ΔE stands for the energy difference between classical and hybrid orbitals, a0 is the Bohr radius, and ζ corresponds to the surface electric field strength. 图 3 外电场中原子和阳离子的杂化轨道与经典轨道的能量差 Fig. 3 The energy difference between hybrid orbitals and classical orbitals of atoms and cations in an external electric field. |
重金属阳离子的3s3pz3dz2轨道在电场中的非对称杂化,产生较低能量的3s+3pz(+)+3dz2和较高能量的3s+3pz(-)+3dz2杂化轨道。在强电场的黏土矿物表面,非对称轨道杂化增加了表面O原子的路易斯(Lewis)碱性,以及吸附的重金属阳离子的Lewis酸性[40]。这是因为对于O原子,电子供体的轨道能量增加了
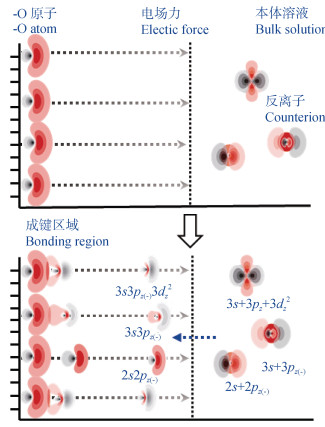
|
图 4 不同类型离子和表面氧(O)原子在带电黏土表面强电场中的界面反应示意图 Fig. 4 Schematic diagram of interface reactions between various types of ions and O atoms in a strong electric field on a charged clay surface. |
当n < 3时(如Na+、Mg2+等),离子与土壤胶体表面仅存在极化增强诱导力(Polarization-enhanced induction force,PEIF);当n ≥ 3时(如K+、Ca2+、Cu2+等),离子与土壤胶体表面同时存在PEIF和PICB。因此,离子-表面相互作用的总能量wT可表示为:
| $ {w_{\text{T}}}{\text{ = }}{w_{{\text{coul}}{\text{.}}}} + {w_{{\text{dipole}}}} + {w_{{\text{cov}}{\text{.}}}} = {\beta _{\text{T}}}ZF{\varphi _0} $ | (6) |
式中,wcoul.、wdipole和wcov.分别为库仑能、来自PEIF的极化能和PICB的共价能,单位J;Z为离子化合价;βT = 1 + wdipole/wcoul. + wcov./wcoul.,表示有效电荷系数,βT的每个分量分别定义为:βcoul. = 1、βdipole = wdipole/wcoul.、βcov. = wcov./wcoul.。
两种反离子混合体系中,离子i和j与表面相互作用均服从此规律,可分别表示为[41]:
| $ \left\{ \begin{gathered} {{\Gamma }_i}\sigma _0^2 = \frac{{\varepsilon RTc_i^0}}{{2\pi {\beta _{\text{T}}}(i)}}\left( {{{\text{e}}^{ - {{{\beta _{\text{T}}}(i)Z(i)F{\varphi _0}} \mathord{\left/ {\vphantom {{{\beta _{\text{T}}}(i)Z(i)F{\varphi _0}} {RT}}} \right. } {RT}}}} - 1} \right) \\ {{\Gamma }_j}\sigma _0^2 = \frac{{\varepsilon RTc_j^0}}{{2\pi {\beta _{\text{T}}}(j)}}\left( {{{\text{e}}^{ - {{{\beta _{\text{T}}}(j)Z(j)F{\varphi _0}} \mathord{\left/ {\vphantom {{{\beta _{\text{T}}}(j)Z(j)F{\varphi _0}} {RT}}} \right. } {RT}}}} - 1} \right) \\ \end{gathered} \right. $ | (7) |
式中,Γi = |σi/σ0|和Γj = |σj/σ0|分别表示离子i和j的吸附率,而且ΣΓ = 1;σi和σj表示单位面积离子i和j的吸附密度,单位C·m–2;ci0和cj0表示本体溶液离子i和j的浓度,单位mol·m–3。
将式(7)中左右两边相加可得,
| $ \sigma _0^{} = \text{sgn} ({\varphi _0})\sqrt {\frac{{\varepsilon RT}}{{2\pi }}\sum\limits_i {\frac{{c_i^0}}{{{\beta _{\text{T}}}(i)}}\left( {{{\text{e}}^{ - {{{\beta _{\text{T}}}(i)Z(i)F{\varphi _0}} \mathord{\left/ {\vphantom {{{\beta _{\text{T}}}(i)Z(i)F{\varphi _0}} {RT}}} \right. } {RT}}}} - 1} \right)} } $ | (8) |
式(8)为考虑轨道杂化效应的表面电位评估表达式。当不考虑轨道杂化效应时,即可返回经典理论(式(5))。
∆Ei/∆Ej表示金属阳离子i与j之间非对称杂化的相对强度。如以j离子为参照,离子i非对称杂化贡献产生的极化能wdipole为:
| $ {w_{{\text{dipole}}}}(i) = \frac{{\Delta {E_i}}}{{{Z_i}\Delta {E_j}}}{\beta _{{\text{dipole}}}}(j){Z_i}F{\varphi _0} $ | (9) |
式中,Zi为金属离子i的化合价。
因此,其他离子的极化贡献可由式(9)进行评估。
相应的能量可表示为:
| $ {w_{{\text{cov}}{\text{.}}}}(i) = {w_{\text{T}}}(i) - {w_{{\text{coul}}{\text{.}}}}(i) - {w_{{\text{dipole}}}}(i) $ | (10) |
土壤胶体表面反离子的浓度决定了反离子与表面O原子相互作用的数量。离子i在颗粒表面的吸附能密度ρi为:
| $ {\rho _i} = {c_i}(0)V{w_{\text{T}}}(i)/(M \times S) = {{ - V\left[ {\frac{{2\pi [1 + {\beta _{\text{T}}}(i)]{\sigma _i}{\sigma _0}}}{\varepsilon } + c_i^0kT} \right]\ln \left( {\frac{{2\pi [1 + {\beta _{\text{T}}}(i)]{\sigma _i}{\sigma _0}}}{{\varepsilon kTc_i^0}} + 1} \right)} \mathord{\left/ {\vphantom {{ - V\left[ {\frac{{2\pi [1 + {\beta _{\text{T}}}(i)]{\sigma _i}{\sigma _0}}}{\varepsilon } + c_i^0kT} \right]\ln \left( {\frac{{2\pi [1 + {\beta _{\text{T}}}(i)]{\sigma _i}{\sigma _0}}}{{\varepsilon kTc_i^0}} + 1} \right)} {(M \times S)}}} \right. } {(M \times S)}} $ | (11) |
式中,ρi表示黏土表面第一层空间离子i的作用力,反映了离子-表面O相互作用的能力,单位J·m–2;V为本体溶液体积,单位m3;M为矿物质量,单位g;S为比表面积,单位m2·g–1。
4 固-液界面原子/离子轨道杂化的土壤环境效应土壤环境效应包括矿物风化与土壤酸化、土壤有机质退化、土壤重金属钝化/活化、污染物迁移与转化、土壤水盐运移、土壤侵蚀、农田面源污染等众多过程。土壤固-液界面反应以及土壤颗粒相互作用对其具有重要影响,而界面反应又受轨道杂化的调控。因此,固-液界面原子/离子轨道杂化对土壤环境具有重要贡献。本文以矿物风化、重金属吸附、水盐运移为例进行分析,旨在为建立微观界面反应与土壤宏观表现的内在关联提供研究思路。
4.1 矿物风化与土壤酸化硅酸盐黏土矿物的溶解反应是自然土壤酸化和矿物风化的重要过程之一[42]。氢离子(H+)是土壤中重要致酸离子之一。质子通过破坏蒙脱石T-O-T层中的桥氧键,释放活化四面体和八面体中的阳离子[43-44],且活化速率随pH降低而增大[45-46],从而促进蒙脱石结构解体。但是,元素释放不服从矿物的化学计量关系[47]。例如,蒙脱石溶解产物的Al/Si摩尔比明显低于纯蒙脱石[48]。研究表明,硅酸盐矿物的基面参与了矿物溶解过程[49],但现有矿物溶解理论无法完全解释该过程的内在机制。
表面电荷产生的强电场使矿物表面O原子与H+之间会产生新的共价性相互作用,即PICB(图 5a)。PICB大大增强了H+吸附能密度(ρH(0),式(11)),且|ρH(0)|随pH降低而增大,表明低pH条件下H+与矿物表面相互作用更强。理论分析与实验结果均表明,H+-矿物的PICB与矿物元素溶出密度的临界pH约为3.0[50]。当pH < 3.0时,PICB明显增强,导致Si-O键能明显减弱,硅酸盐矿物的溶解大幅提高。尽管不同矿物的元素溶出密度随pH的变化表现出较大差异,但其与ρH(0)的关系均服从同一规律(图 5b),表明ρH(0)对黏土矿物结构具有重要影响。H+-矿物极化诱导共价作用增强了H+-矿物表面O原子的ρH(0)而减弱矿物Si-O键能,从而促进矿物结构解体。值得一提的是,实验上矿物溶解速率是在pH低于3时才显著增加,自然界中很少存在如此强的酸性环境。但是,较高pH条件下矿物结构缓慢变化,经过长时期的积累,盐基离子的淋失,铝离子的水解会产生更多H+,从而提高|ρH(0)|和风化速率。
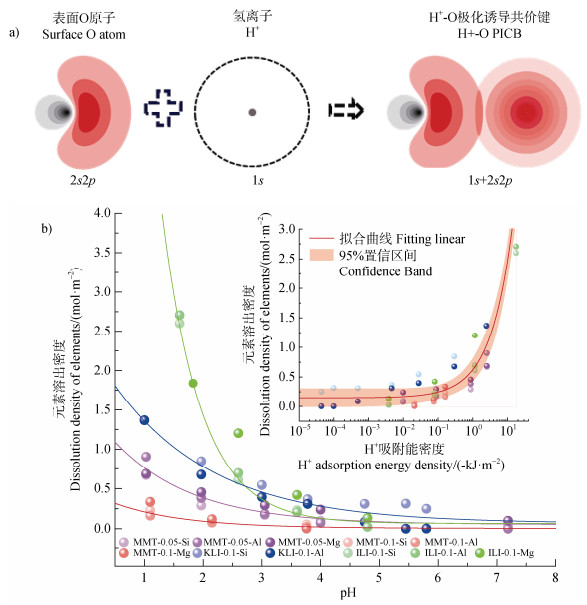
|
注:图例中0.05、0.1、1和0.1分别为背景电解质的浓度为0.05、0.1、1和0.1 mol·L–1。实线是拟合的趋势线,数据来源于文献[50]。 Note: The symbols 0.05, 0.1, 1, and 0.1 in the figure legend are the background electrolyte concentrations of 0.05, 0.1, 1, and 0.1 mol·L‒1, respectively. The lines are the fitted trend curves. Data were cited from the reference[50]. 图 5 H+与矿物表面O原子相互作用示意图(a)以及蒙脱石(MMT)、高岭石(KLI)、伊利石(ILI)中元素溶出密度与pH和H+吸附能密度的关系(b) Fig. 5 Schematic diagram of H+-O atoms on the mineral surface (a), the dissolution density variations of mineral elements in montmorillonite (MMT), illite (ILI), and kaolinite (KLI) as a function of pH and H+ adsorption energy density (b) |
轨道杂化效应在H+与矿物相互作用中具有重要贡献,加速了矿物化学风化进程。硅酸盐矿物风化是土壤自然酸化的核心驱动过程,其作用贯穿土壤发育的不同阶段,从而使我国土壤总体呈现“南酸北碱”的地带性分布特征[51]。酸沉降、化学氮肥的不合理施用等均能引起土壤酸化[52-53]。对土壤酸化的改良,通过调控H+与矿物相互作用防止矿物结构解体,至少有以下三种途径可以实现:(1)降低H+浓度,增加盐基离子浓度,提高盐基离子与表面相互作用,减弱H+对矿物结构的破坏;(2)增加羟基型表面,形成有机-无机复合体,降低H+与矿物表面O的相互作用,提高土壤酸缓冲能力;(3)增大比表面积和/或减小表面电荷数量,降低表面电场,减弱矿物表面O原子的电子活性,从而降低H+与表面O的相互作用。
要实现对以上途径的定向调控,需准确评估H+与表面的相互作用力,而轨道杂化效应对该作用力具有重要影响。因此,土壤固-液界面轨道杂化效应对矿物风化和土壤酸化具有重要的调控作用。
4.2 土壤重金属钝化/活化重金属离子与矿物相互作用是重金属吸附/解吸的重要驱动力,对土壤重金属的钝化/活化具有重要影响。基于上述原理(式(6)~ 式(10)),评估了几种金属离子在矿物表面的库仑力、极化力和极化诱导共价键在总吸附能中的贡献(图 6)。
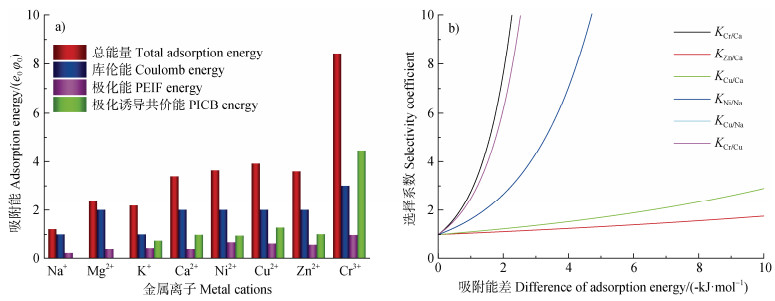
|
注:数据来源于文献[6-7]。 Note: Data are sourced from references[6-7]. 图 6 几种金属离子在蒙脱石表面的库仑力、极化增强诱导力(PEIF)和极化诱导共价键(PICB)在总吸附能中的贡献(a)及金属离子吸附选择系数与吸附能量差的关系(b) Fig. 6 Contributions of Coulombic force, polarization-enhanced induction force (PEIF), and polarization-induced covalent bonding (PICB) to the total adsorption energy of several metal cations on a montmorillonite surface (a), and adsorption selectivity coefficient of metal cations as a function of adsorption energy difference (b) |
图 6a表明,蒙脱石表面金属离子存在不同程度的极化或/和极化诱导共价作用,与离子的化合价和外层电子排布密切相关。Na+和Mg2+为外层2s2p轨道杂化,K+和Ca2+为外层3s3p轨道杂化,而Ni+、Cu2+、Zn2+和Cr3+为外层3s3p3d轨道杂化。杂化效应的差异决定了金属离子在蒙脱石表面各作用力中的贡献。
根据吸附平衡模型[54],定量表征重金属的吸附选择性,结果如图 6b所示。尽管表面类型对金属离子选择性吸附具有一定影响,但是带电表面强电场中金属离子外层轨道杂化效应是吸附选择性的重要原因之一。吸附选择性随吸附能量差的升高而增大,当能量差为0时,选择系数为1,即不存在吸附选择性(图 6b)。重金属在羟基型表面存在强烈的共价作用(为了区分,称为经典共价键),即使表面不带电,经典共价作用仍然存在[55],也会使重金属离子存在吸附选择性[56]。当表面电场存在时,吸附态的重金属离子轨道发生杂化效应,吸附选择性会进一步增强。因此,经典共价键和极化诱导共价键共同影响重金属在羟基型表面的吸附。
钝化/活化是土壤重金属污染修复的重要途径之一,其效果受到重金属离子的表面吸附能控制。因此,在实际应用中,可通过调节土壤颗粒表面电场调控吸附态重金属的轨道杂化效应,通过表面电荷类型调节重金属在颗粒表面的共价作用。
4.3 土壤水盐运移由前面分析可知,轨道杂化效应对土壤颗粒表面电位具有重要影响,而表面电位通过影响土壤颗粒间的中点电位,控制土壤颗粒间静电排斥力:
| $ {P_{{\text{EDL}}}} = \sum {\frac{{c_i^0RT}}{{{\beta _{\text{T}}}(i)}}\left[ {{e^{ - {{{Z_i}F{\varphi _d}} \mathord{\left/ {\vphantom {{{Z_i}F{\varphi _d}} {(RT)}}} \right. } {(RT)}}}} - 1} \right]} $ | (12) |
式中,φd为相邻两土壤颗粒间中点位置的电位,单位V;对称电解质体系下φd由下式计算:
| $ \begin{gathered} \frac{\pi }{2}\left[ {1 + {{\left( {\frac{1}{2}} \right)}^2}{e^{\frac{{2{Z_i}F{\varphi _d}}}{{RT}}}} + {{\left( {\frac{3}{8}} \right)}^2}{e^{\frac{{4{Z_i}F{\varphi _d}}}{{RT}}}}} \right] - \hfill \\ \arcsin {e^{\frac{{{Z_i}F{\varphi _0} - {Z_i}F{\varphi _d}}}{{2RT}}}} = \frac{1}{2}d\kappa {e^{\frac{{ - {Z_i}F{\varphi _d}}}{{2RT}}}} \hfill \\ \end{gathered} $ | (13) |
2︰1型电解质体系下φd由下式计算:
| $ {e^{\frac{{F{\varphi _d}}}{{RT}}}}\sqrt {1 - {e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}}} \left[ {\frac{2}{3} - \frac{1}{6}{e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}} + \left( {\frac{3}{8} + {e^{\frac{{3F{\varphi _d}}}{{RT}}}}} \right)\left( {\frac{1}{3} + \frac{2}{3}{e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}} + \frac{1}{5}{{\left( {1 - {e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}}} \right)}^2}} \right)} \right] = d\sqrt {\frac{{2\pi {F^2}c_j^0}}{{\varepsilon RT}}} $ | (14) |
一价与二价反离子的混合体系下φd由下式计算:
| $ {e^{\frac{{F{\varphi _d}}}{{RT}}}}\sqrt {1 - {e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}}} \left[ \begin{gathered} 1 - \frac{1}{6}\left( {\frac{{\sum {{c_i}} }}{{\sum {{c_j}} }}{e^{\frac{{F{\varphi _d}}}{{RT}}}} + 1} \right)\left( {2 + {e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}}} \right) \hfill \\ + \left[ {\frac{3}{8}{{\left( {\frac{{\sum {{c_i}} }}{{\sum {{c_j}} }}{e^{\frac{{F{\varphi _d}}}{{RT}}}} + 1} \right)}^2} + \frac{1}{2}{e^{\frac{{3F{\varphi _d}}}{{RT}}}}\left( {\frac{{\sum {{c_i}} }}{{\sum {{c_j}} }} + 2} \right)} \right]\left( {\frac{1}{3} + \frac{2}{3}{e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}} + \frac{1}{5}{{\left( {1 - {e^{\frac{{F({\varphi _0} - {\varphi _d})}}{{RT}}}}} \right)}^2}} \right) \hfill \\ \end{gathered} \right]{\text{ = }}\sqrt {\frac{{2\pi {F^2}\sum {c_j^0} }}{{\varepsilon RT}}} d $ | (15) |
式中,cj0为本体溶液离子i和j的浓度,单位mol·m–3;∑ci和∑cj分别为土壤溶液中一价反离子和二价反离子之和;d为颗粒表面至中点位置的距离,单位m。一般情况下,土壤中主要含有一价和二价反离子,因此可通过式(12)和式(15)评估田间条件下土壤颗粒间的静电排斥压。
上式表明基于轨道杂化效应的表面电位评估后,即可对土壤颗粒间的静电排斥压进行定量表征。1︰1电解质体系下电位分布可由式(1)和式(2)获得。轨道杂化效应使同价离子间的土壤静电排斥力存在差异,杂化效应强的离子(如K+)显著降低静电排斥力,从而使杂化效应强的K+体系的静电排斥压显著低于杂化效应弱的Na+体系(图 7a)。土壤颗粒间静电排斥压对土壤孔隙大小和分布具有重要调控作用,K+体系较低的排斥压使土壤团聚体更稳定,从而使大于0.5 mm的土壤孔隙比例较Na+体系更多;Na+体系较高的排斥压使土壤团聚体更容易分散成小颗粒,堵塞土壤孔隙,从而使小于0.5 mm的土壤孔隙比例较K+体系更多(图 7b)。孔隙大小与分布决定了土壤中水分的入渗速率,Na+含量高和电解质浓度较低的体系,排斥压更高,土壤小孔隙居多,土壤水分入渗更慢;相反,水分入渗则更快(图 7c)。从理论上解析了离子轨道杂化效应-颗粒间相互作用力-土壤孔隙分布-水分运动的多尺度内在关联。水分入渗在盐碱土以及漠土治理具有重要的理论和现实意义。图 7的结果可得出推论:水是盐碱土洗盐的必要条件,但不是充分条件。因此,在盐碱土改良过程中,降低土壤颗粒间静电排斥力是关键途径之一。
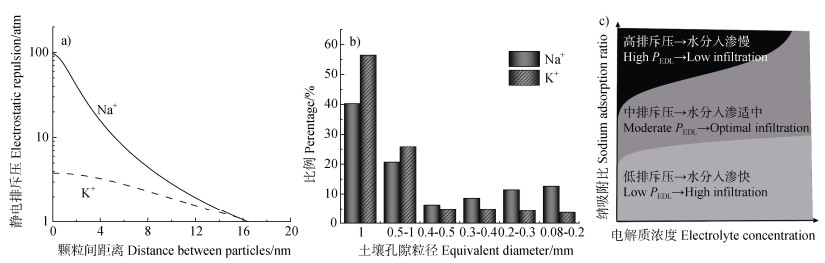
|
注:PEDL为排斥压,数据来源于文献[17]。 Note: PEDL is the exclusion pressure, and the data are sourced from the reference[17]. 图 7 Na+和K+体系土壤颗粒静电排斥压与土壤颗粒间距离的关系(a)、Na+和K+体系土壤各粒径孔隙占总孔隙的比例(b)及钠吸附比和电解质浓度影响土壤颗粒静电排斥压调控土壤水分入渗(c) Fig. 7 Electrostatic repulsive pressure as a function of distance between soil particles in Na+ and K+ systems (a), proportion of pores in different size fractions relative to the total porosity in Na+ and K+ systems (b), and influence of sodium adsorption ratio and electrolyte concentration on the regulation of soil water infiltration through electrostatic repulsion pressure between soil particles (c) |
同样,高排斥压的Na+体系,土壤团聚体分散导致颗粒态磷的迁移量远远大于低排斥压的K+体系(图 8a)。当土壤颗粒间1.5 nm处静电排斥压超过2.5 MPa时,土壤颗粒态磷迁移量急剧增大(图 8b),表明电解质类型和浓度通过土壤颗粒间相互作用力调控了土壤中磷的迁移[57]。土壤中磷迁移进入水体,容易导致富营养化。值得一提的是,由于磷的专性吸附,磷的迁移主要随土壤颗粒一起迁移。因此,农田面源污染的防控应着重关注土壤内部颗粒相互作用驱动的水-土-溶质迁移。
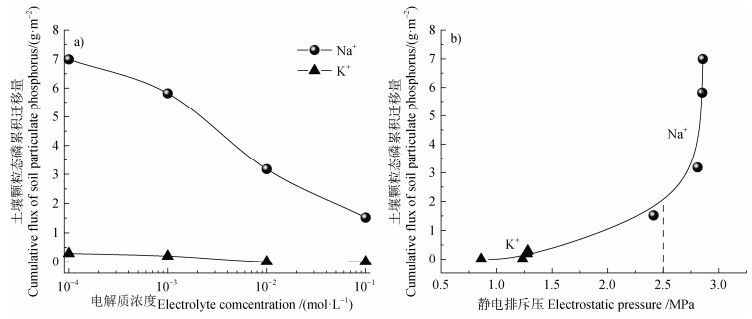
|
注:数据来源于文献[58]。 Note: Data are sourced from reference[58]. 图 8 土壤颗粒态磷的迁移与电解质浓度(a)和土壤颗粒间静电排斥压(b)的关系 Fig. 8 Cumulative flux of soil particulate phosphorus (PP) as a function of electrolyte concentration (a) and electrostatic repulsion pressure between soil particles (b) |
虽然仅列举了Na+和K+体系进行阐述,但实际上在其他体系中也存在类似规律,且土壤中众多宏观过程均与土壤颗粒相互作用有关。例如,可通过调节土壤颗粒相互作用力调控土壤胶体的凝聚与分散[59],影响土壤团聚体和有机-无机复合体的形成与稳定[60-61],以及土壤侵蚀[20],在耕地质量提升和水土保持方面具有重要作用。同时结合外部措施,实现“内外力”的联合防控。其中“内力”作用之一即为依赖于离子轨道杂化效应的土壤颗粒间静电排斥力。
5 结论与展望基于经典基础科学原理建立的界面反应理论和颗粒相互作用理论未能充分考虑土壤体系固有的特殊性,即黏土矿物独特的化学组成、晶体结构以及表面强电场。土壤固-液界面中离子存在依赖于表面电场和量子效应的附加位能,这表明土壤是一个独特的“量子力学”系统。量子力学分析发现,土壤矿物颗粒表面存在强烈的原子/离子轨道杂化效应,该效应影响离子与表面的相互作用,进而调控土壤环境中的界面过程(如H+-土壤/矿物相互作用主导的土壤酸化和矿物风化过程,重金属离子-土壤/矿物相互作用调控的土壤重金属钝化/活化过程等)。同时,微观尺度的轨道杂化效应可通过改变土壤固-液界面性质及反应,进而影响介观尺度土壤颗粒间相互作用,调控宏观尺度土壤环境过程,如土壤团聚体稳定性、水土流失、农田面源污染、土壤酸化和有机质退化等。因此,土壤固-液界面轨道杂化效应作为调控界面性质和土壤“内力”的核心机制,在土壤改良与农业环境保护等方面扮演着关键角色。结合土壤外部调控措施,实现“内外力”协同调控,是改善土壤环境与质量、促进农业绿色可持续发展的有效途径。
土壤固-液界面原子/离子轨道杂化效应本质上是土壤电场与原子相互作用的结果。未来研究亟需在以下几方面加强:
1)现代分析技术与量子力学理论协同揭示基于轨道杂化的表面反应机制。目前固-液界面的轨道杂化效应尚缺乏直接的实验验证,还需结合现代分析技术,例如同步辐射X射线、高分辨显微镜(如透射电镜、原子力显微镜)、X射线光电子能谱、穆斯堡尔谱等技术手段,共同验证离子/原子杂化轨道的构型变化及其与表面的相互作用。
2)构建水-土-溶质迁移精准预测预报模型。当前土壤水-土-溶质迁移的高精度连续监测数据匮乏,制约了预测预报模型的构建和完善。因此,亟需在不同尺度开展同步试验和监测。由于土壤“内力”的原位评估及其对水-土-溶质迁移影响的系统研究严重缺失,传统认知主要强调外力驱动,导致依赖外部措施的监测技术难以实现精准预测和及时预报,内力评估与外部监测相结合是关键。因此,深入研究基于“电场-原子”相互作用的土壤“内力”与水-土-溶质迁移的定量关系,是构建高精度水-土-溶质迁移预测预报模型的核心环节。
3)揭示土壤微观过程与宏观表现的多尺度关联机制。土壤微观过程与宏观表现的研究长期脱节,基础理论的普适性不足是其关键瓶颈。以“电场-原子”相互作用的量子力学表征为突破口,建立普适性的土壤学基础理论框架,可能是实现从亚原子/原子量子行为→土壤微观过程→宏观表现的多尺度多过程内在关联研究的必由之路,从而有效服务土壤固碳减排、耕地质量提升、土壤退化阻控和污染修复等国家重大需求。
4)构建基于量子力学的土壤学核心知识体系。土壤学作为独立学科亟需构建独特的核心理论框架。土壤是天然的强电场体系,其固-液界面存在的原子/离子轨道杂化效应揭示了其内在独特的量子特性。未来应系统深化“电场-原子”相互作用研究,为构建土壤学核心知识体系奠定理论基础。
| [1] |
Kang M G, Choi J G, Jeong J, et al. Electric-field control of field-free spin-orbit torque switching via laterally modulated Rashba effect in Pt/Co/AlOx structures[J]. Nature Communications, 2021, 12: 7111. DOI:10.1038/s41467-021-27459-2
(  0) 0) |
| [2] |
Chakhalian J, Freeland J W, Habermeier H U, et al. Orbital reconstruction and covalent bonding at an oxide interface[J]. Science, 2007, 318(5853): 1114-1117. DOI:10.1126/science.1149338
(  0) 0) |
| [3] |
Liu D, Tian R, Feng B, et al. Polarisation-induced covalent interactions between H+ and surface O atoms promote clay aggregation[J]. European Journal of Soil Science, 2022, 73(4): e13286. DOI:10.1111/ejss.13286
(  0) 0) |
| [4] |
Bedrov D, Piquemal J P, Borodin O, et al. Molecular dynamics simulations of ionic liquids and electrolytes using polarizable force fields[J]. Chemical Reviews, 2019, 119(13): 7940-7995. DOI:10.1021/acs.chemrev.8b00763
(  0) 0) |
| [5] |
Oak M A, Lee J H, Jang H M, et al. 4d-5p orbital mixing and asymmetric in 4d-O 2p hybridization in InMnO3: A new bonding mechanism for hexagonal ferroelectricity[J]. Physical Review Letters, 2011, 106(4): 047601. DOI:10.1103/PhysRevLett.106.047601
(  0) 0) |
| [6] |
Liu X M, Chen W L, Tang Y, et al. Asymmetric response of transition metal cationic orbitals to applied electric field[J]. Journal of Hazardous Materials, 2024, 468: 133718. DOI:10.1016/j.jhazmat.2024.133718
(  0) 0) |
| [7] |
Liu X M, Tang Y, Tian R, et al. Asymmetric orbital hybridization promotes polarization and covalent interactions between heavy metal cations and charged surfaces[J]. Applied Surface Science, 2024, 656: 159689. DOI:10.1016/j.apsusc.2024.159689
(  0) 0) |
| [8] |
Wang L, Tang Y, Ding W Q, et al. A how-to approach to estimating surface charge density of nano/micro particles through aggregation experiments considering the specific ion effect[J]. Langmuir, 2025, 41(10): 6612-6620. DOI:10.1021/acs.langmuir.4c04477
(  0) 0) |
| [9] |
Yin H, Yin M, Yan X R, et al. Recent advances in heavy metal isotope fractionation behaviors at the interfaces of soil active components (In Chinese)[J]. Journal of Nuclear Agricultural Sciences, 2024, 38(3): 603-611. [殷辉, 殷明, 严欣然, 等. 土壤活性组分界面重金属同位素分馏行为研究进展[J]. 核农学报, 2024, 38(3): 603-611.]
(  0) 0) |
| [10] |
Lee W H, Yoon S G, Jin H D, et al. Electron density‐change in semiconductor by ion‐adsorption at solid–liquid interface[J]. Advanced Materials, 2021, 33(10): 2007581. DOI:10.1002/adma.202007581
(  0) 0) |
| [11] |
Lyu D X, Märker K, Zhou Y N, et al. Understanding sorption of aqueous electrolytes in porous carbon by NMR spectroscopy[J]. Journal of the American Chemical Society, 2024, 146(14): 9897-9910. DOI:10.1021/jacs.3c14807
(  0) 0) |
| [12] |
Xiao S, Qu J W, Tang Y T, et al. Electric-field-dependent covalent interactions between H+ and surface O atoms promote the structural disintegration of montmorillonite[J]. Langmuir, 2025, 41(20): 12607-12618. DOI:10.1021/acs.langmuir.5c00671
(  0) 0) |
| [13] |
Li H, Liu X M, Tian R, et al. Thoughts for the reconstruction of core knowledge system of basic soil science: Necessity, theoretical and methodological basis (In Chinese)[J]. Acta Pedologica Sinica, 2025, 62(1): 1-13. DOI:10.11766/trxb202403120105 [李航, 刘新敏, 田锐, 等. 基于量子力学的基础土壤学核心知识体系重建的若干思考: 必要性及理论与方法基础[J]. 土壤学报, 2025, 62(1): 1-13.]
(  0) 0) |
| [14] |
Ali W, Hussain S, Chen J Z, et al. Cover crop root-derived organic carbon influences aggregate stability through soil internal forces in a clayey red soil[J]. Geoderma, 2023, 429: 116271. DOI:10.1016/j.geoderma.2022.116271
(  0) 0) |
| [15] |
Li S, Wang B L, Zhang X, et al. Soil particle aggregation and aggregate stability associated with ion specificity and organic matter content[J]. Geoderma, 2023, 429: 116285. DOI:10.1016/j.geoderma.2022.116285
(  0) 0) |
| [16] |
Yu Z H, Zheng Y Y, Zhang J B, et al. Importance of soil interparticle forces and organic matter for aggregate stability in a temperate soil and a subtropical soil[J]. Geoderma, 2020, 362: 114088. DOI:10.1016/j.geoderma.2019.114088
(  0) 0) |
| [17] |
Ding W Q, Liu X M, Hu F N, et al. How the particle interaction forces determine soil water infiltration: Specific ion effects[J]. Journal of Hydrology, 2019, 568: 492-500. DOI:10.1016/j.jhydrol.2018.11.017
(  0) 0) |
| [18] |
Wu Y B, Zhang Z, Li X F, et al. The influence of ion interface reaction on the permeability pressure characteristics of typical granite benggang sandy loam red soil layer in Anxi County (In Chinese)[J]. Acta Pedologica Sinica, 2025, 62(2): 411-421. DOI:10.11766/trxb202401040012 [吴云博, 章智, 李晓非, 等. 离子界面反应对安溪县典型花岗岩崩岗砂壤红土层渗压特性的影响[J]. 土壤学报, 2025, 62(2): 411-421.]
(  0) 0) |
| [19] |
Wang Y, Zhang W, Shang J Y, et al. Chemical aging changed aggregation kinetics and transport of biochar colloids[J]. Environmental Science & Technology, 2019, 53(14): 8136-8146.
(  0) 0) |
| [20] |
Ma R T, Hu F N, Xu C Y, et al. Vegetation restoration enhances soil erosion resistance through decreasing the net repulsive force between soil particles[J]. Catena, 2023, 226: 107085. DOI:10.1016/j.catena.2023.107085
(  0) 0) |
| [21] |
Wang Q, Wen J, Wen Y J, et al. Alteration of soil-surface electrochemical properties by organic fertilization to reduce dissolved inorganic nitrogen leaching in paddy fields[J]. Soil & Tillage Research, 2021, 209: 104956.
(  0) 0) |
| [22] |
Liu X M, Li H, Li R, et al. Strong non-classical induction forces in ion-surface interactions: General origin of Hofmeister effects[J]. Scientific Reports, 2014, 4: 5047. DOI:10.1038/srep05047
(  0) 0) |
| [23] |
Yu T R
. Electrochemical properties of soil and their research methods (In Chinese). 2nd ed[M]. Beijing: Science Press, 1976. [于天仁
. 土壤的电化学性质及其研究法[M]. 2版. 北京: 科学出版社, 1976.]
(  0) 0) |
| [24] |
Sposito G
. The surface chemistry of soils . Oxford/New York: Clarendon Press/Oxford Univ Press, 1984.
(  0) 0) |
| [25] |
Li X, Li H, Yang G. Electric fields within clay materials: How to affect the adsorption of metal ions[J]. Journal of Colloid and Interface Science, 2017, 501: 54-59. DOI:10.1016/j.jcis.2017.04.040
(  0) 0) |
| [26] |
Liu X M, Hu F N, Ding W Q, et al. A how-to approach for estimation of surface/Stern potentials considering ionic size and polarization[J]. Analyst, 2015, 140(21): 7217-7224. DOI:10.1039/C5AN01053E
(  0) 0) |
| [27] |
Gouy G. Constitution of the electric charge at the surface of an electrolyte[J]. Le Journal de Physique et le Radium, 1910, 9: 457-467.
(  0) 0) |
| [28] |
Chapman D L. LI. A contribution to the theory of electrocapillarity[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1913, 25(148): 475-481. DOI:10.1080/14786440408634187
(  0) 0) |
| [29] |
Grahame D C. Effects of dielectric saturation upon the diffuse double layer and the free energy of hydration of ions[J]. The Journal of Chemical Physics, 1950, 18(7): 903-909. DOI:10.1063/1.1747807
(  0) 0) |
| [30] |
Liu X M, Li H, Li R, et al. Analytical solutions of the nonlinear Poisson–Boltzmann equation in mixture of electrolytes[J]. Surface Science, 2013, 607: 197-202. DOI:10.1016/j.susc.2012.09.008
(  0) 0) |
| [31] |
Zhao X N, Zhou X L, Cao C X, et al. Plasmonic in situ imaging of Zeta potential distributions at electrochemical interfaces of 2D materials in water[J]. Nature Communications, 2025, 16: 3494. DOI:10.1038/s41467-025-58793-4
(  0) 0) |
| [32] |
Gopmandal P P, Duval J F L. Electrostatics and electrophoresis of engineered nanoparticles and particulate environmental contaminants: Beyond Zeta potential-based formulation[J]. Current Opinion in Colloid & Interface Science, 2022, 60: 101605.
(  0) 0) |
| [33] |
Serrano-Lotina A, Portela R, Baeza P, et al. Zeta potential as a tool for functional materials development[J]. Catalysis Today, 2023, 423: 113862. DOI:10.1016/j.cattod.2022.08.004
(  0) 0) |
| [34] |
Li H, Chang L Q, Wei S Q, et al. An approach to the method for determination of surface potential on solid/liquid interface: Theory[J]. Journal of Colloid and Interface Science, 2004, 275(1): 172-176. DOI:10.1016/j.jcis.2003.12.055
(  0) 0) |
| [35] |
Liu X M, Tian R, Li R, et al. Principles for the determination of the surface potential of charged particles in mixed electrolyte solutions[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2015, 471(2180): 20150064. DOI:10.1098/rspa.2015.0064
(  0) 0) |
| [36] |
Zeng J Y
. Course of quantum mechanics (In Chinese). 3rd ed[M]. Beijing: Science Press, 2014. [曾谨言
. 量子力学教程[M]. 3版. 北京: 科学出版社, 2014.]
(  0) 0) |
| [37] |
Li Q Y, Yang S, Tang Y, et al. Asymmetric hybridization orbitals at the charged interface initiates new surface reactions: A quantum mechanics exploration[J]. The Journal of Physical Chemistry C, 2019, 123(41): 25278-25285. DOI:10.1021/acs.jpcc.9b07874
(  0) 0) |
| [38] |
Zhou G D, Duan L Y
. Fundamentals of structural chemistry (In Chinese). 4th ed[M]. Beijing: Peking University Press, 2008. [周公度, 段连运
. 结构化学基础[M]. 4版. 北京: 北京大学出版社, 2008.]
(  0) 0) |
| [39] |
Xu G X, Zhao X Z. Modified Slater's method for the calculation of the ionization energies of atoms (In Chinese)[J]. Acta Chimica Sinica, 1956, 22(6): 441. [徐光宪, 赵学庄. Slater型原子轨函和电离能的近似计算法的改进[J]. 化学学报, 1956, 22(6): 441.]
(  0) 0) |
| [40] |
Li Q Y, Liu X M, Shi W Y. Orbital asymmetric hybridization enhances surface Lewis acid-base reactions of charged clay catalysts[J]. Applied Surface Science, 2022, 575: 151731. DOI:10.1016/j.apsusc.2021.151731
(  0) 0) |
| [41] |
Liu X M, Yang T, Li H, et al. Effects of interactions between soil particles and electrolytes on saturated hydraulic conductivity[J]. European Journal of Soil Science, 2020, 71(2): 190-203. DOI:10.1111/ejss.12855
(  0) 0) |
| [42] |
Vicca S, Goll D S, Hagens M, et al. Is the climate change mitigation effect of enhanced silicate weathering governed by biological processes?[J]. Global Change Biology, 2022, 28(3): 711-726. DOI:10.1111/gcb.15993
(  0) 0) |
| [43] |
Cappelli C, Yokoyama S, Cama J, et al. Montmorillonite dissolution kinetics: Experimental and reactive transport modeling interpretation[J]. Geochimica et Cosmochimica Acta, 2018, 227: 96-122. DOI:10.1016/j.gca.2018.01.039
(  0) 0) |
| [44] |
Schott J, Saldi G D, Zhu C, et al. Mechanisms controlling albite dissolution/precipitation kinetics as a function of chemical affinity: New insights from experiments in 29Si spiked solutions at 150 and 180 ℃[J]. Geochimica et Cosmochimica Acta, 2024, 374: 284-303. DOI:10.1016/j.gca.2024.03.023
(  0) 0) |
| [45] |
Li K W, Xu R K. Effect of aluminum oxides on the activation of aluminum during phyllosilicate minerals and red soil acidification (In Chinese)[J]. Acta Pedologica Sinica, 2024, 61(6): 1557-1567. DOI:10.11766/trxb202311260497 [李科伟, 徐仁扣. 铝氧化物对层状硅酸盐矿物和红壤酸化过程中铝活化的影响[J]. 土壤学报, 2024, 61(6): 1557-1567.]
(  0) 0) |
| [46] |
Chen M M, Zhang S R, Liu L, et al. Influence of organic fertilization on clay mineral transformation and soil phosphorous retention: Evidence from an 8-year fertilization experiment[J]. Soil and Tillage Research, 2023, 230: 105702. DOI:10.1016/j.still.2023.105702
(  0) 0) |
| [47] |
Zhao Y, Yang J L, Xu Z, et al. Stoichiometry of base cations and silicon of cambosols derived from different parent materials as leached by simulated acid rain (In Chinese)[J]. Acta Pedologica Sinica, 2023, 60(5): 1456-1467. DOI:10.11766/trxb202202110053 [赵越, 杨金玲, 许哲, 等. 模拟酸雨淋溶下不同母质发育雏形土矿物风化中的盐基离子与硅计量关系[J]. 土壤学报, 2023, 60(5): 1456-1467.]
(  0) 0) |
| [48] |
Metz V, Amram K, Ganor J. Stoichiometry of smectite dissolution reaction[J]. Geochimica et Cosmochimica Acta, 2005, 69(7): 1755-1772. DOI:10.1016/j.gca.2004.09.027
(  0) 0) |
| [49] |
Grybos M, Michot L J, Skiba M, et al. Dissolution of anisotropic colloidal mineral particles: Evidence for basal surface reactivity of nontronite[J]. Journal of Colloid and Interface Science, 2010, 343(2): 433-438. DOI:10.1016/j.jcis.2009.11.058
(  0) 0) |
| [50] |
Tang Y T, Xiao S, Ding W Q, et al
. Polarization‐ induced covalent bonding between H+ and surface O atoms promotes clay mineral dissolution (In Chinese)[J]. Acta Pedologica Sinica, 2026. DOI:10.11766/trxb202501090018 [唐雨婷, 肖爽, 丁武泉, 等
. H+与表面氧原子的极化诱导共价作用促进黏土矿物溶解[J]. 土壤学报, 2026.]
(  0) 0) |
| [51] |
Chen S C, Liang Z Z, Webster R, et al. A high-resolution map of soil pH in China made by hybrid modelling of sparse soil data and environmental covariates and its implications for pollution[J]. Science of the Total Environment, 2019, 655: 273-283. DOI:10.1016/j.scitotenv.2018.11.230
(  0) 0) |
| [52] |
Blake L, Goulding K W T, Mott C J B, et al. Changes in soil chemistry accompanying acidification over more than 100 years under woodland and grass at Rothamsted Experimental Station, UK[J]. European Journal of Soil Science, 1999, 50(3): 401-412. DOI:10.1046/j.1365-2389.1999.00253.x
(  0) 0) |
| [53] |
Guo J H, Liu X J, Zhang Y, et al. Significant acidification in major Chinese croplands[J]. Science, 2010, 327(5968): 1008-1010. DOI:10.1126/science.1182570
(  0) 0) |
| [54] |
Liu X M, Li H, Du W, et al. Hofmeister effects on cation exchange equilibrium: Quantification of ion exchange selectivity[J]. The Journal of Physical Chemistry C, 2013, 117(12): 6245-6251. DOI:10.1021/jp312682u
(  0) 0) |
| [55] |
Bagus P S, Nelin C J, Hrovat D A, et al. Covalent bonding in heavy metal oxides[J]. Journal of Chemical Physics, 2017, 146(13): 134706. DOI:10.1063/1.4979018
(  0) 0) |
| [56] |
Covelo E F, Andrade M L, Vega F A. Heavy metal adsorption by humic umbrisols: Selectivity sequences and competitive sorption kinetics[J]. Journal of Colloid and Interface Science, 2004, 280(1): 1-8. DOI:10.1016/j.jcis.2004.07.024
(  0) 0) |
| [57] |
Hu L, Du W, Chang B K, et al. The surface properties of Lou soil with different phosphorus levels and their effects on the loss of phosphorus (In Chinese)[J]. Acta Pedologica Sinica, 2023, 60(2): 424-434. DOI:10.11766/trxb202107070349 [胡良, 杜伟, 常博焜, 等. 不同磷水平塿土的表面性质及其对磷素流失特征的影响[J]. 土壤学报, 2023, 60(2): 424-434.]
(  0) 0) |
| [58] |
Xie P L, Tan L, Li H, et al. Effects of soil electric field and mechanical composition on soil phosphorus migration (In Chinese)[J]. Journal of Environmental Engineering, 2024, 18(3): 886-896. [谢佩玲, 谭立, 李航, 等. 土壤电场和机械组成对土壤磷迁移的影响[J]. 环境工程学报, 2024, 18(3): 886-896.]
(  0) 0) |
| [59] |
Zhang Y W, Tian R, Wu W F, et al
. Study on colloidal properties of purple soil and its aggregation kinetics under different fertilization treatments (In Chinese)[J]. Acta Pedologica Sinica, 2026. DOI:10.11766/trxb202411010420 [张一炜, 田锐, 吴文菲, 等
. 不同施肥处理紫色土胶体性质及其凝聚动力学研究[J]. 土壤学报, 2026.]
(  0) 0) |
| [60] |
Even R J, Cotrufo M F. The ability of soils to aggregate, more than the state of aggregation, promotes protected soil organic matter formation[J]. Geoderma, 2024, 442: 116760. DOI:10.1016/j.geoderma.2023.116760
(  0) 0) |
| [61] |
Li X D, Wang R Y, Dai W, et al. Aging microplastics and coupling of "microplastic-electric fields" can affect soil water-stable aggregates' stability[J]. Journal of Hazardous Materials, 2024, 469: 134048. DOI:10.1016/j.jhazmat.2024.134048
(  0) 0) |
 2026, Vol. 63
2026, Vol. 63

